1. Introduction
X2O3 (X:Gd, Tb) are the interesting materials from both fundamental and industrial perspectives and have a wide range of applications. They are thermodynamically stable, making them useful for corrosion resistive coating [1] -[5] . Additionally, their high refractive indices lead to applications in optics, such as antireflection coatings, switches, filters and modulators [1] [4] . The most recent interest of them is due to their high dielectric constants and electrical stability, making them good candidates for a new class of gate oxides in metal-oxide semiconductor field-effect transistors [1] . In addition, many properties of rare-earth sesquioxides are determined by their semicore f-levels. While being mainly localized on the rare-earth atoms and usually not participating in bonding and electronic conduction, f-shell electrons are available for optical transition and can establish strong magnetic order [1] . So far as we know, no ab initio general potential calculation of the optical properties of the rare-earth sesquioxides has been reported. The main purpose of this work is to provide some additional information to the existing features of Gd2O3 and Tb2O3 by using density functional theory. Therefore, in this work, we have investigated the electronic and optical properties of Gd2O3 and Tb2O3 compounds.
2. Method of Calculation
In the present paper, all calculations have been carried out using the ab-initio total-energy and molecular-dy- namics program VASP (Vienna ab-initio simulation program) developed at the Faculty of Physics of the University of Vienna [6] - [9] within the density functional theory (DFT) [10] . The exchange-correlation energy function is treated within the GGA (generalized gradient approximation) by the density functional of Perdew et al. [11] . We get a good convergence using a 
Monkhorst-Pack [12] mesh grid for the total-energy calculation with a cutoff energy of 510 eV for both compunds. The electronic iterations convergence is 
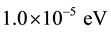using the Normal (blocked Davidson) algorithm and reciprocal space projection operators. These values were found to be sufficient for studying the electronic and optical properties of X2O3 crystals.
3. Results and Discussion
3.1. Structural and Electronic Properties
In the first step of our calculations, we have carried out the equilibrium lattice constants of Gd2O3, and Tb2O3 by minimizing the ratio of the total energy of the crystal to its volume using the experimental data [13] [15] . We have compared the present results for lattice parameters of X2O3 with previous experimental values [13] - [29] and are given in Table 1. These results are within the accuracy range of calculations based on density functional theory.
![]()
Table 1. The calculatedequilibriumlattice parameters and direct band gaps together with the available experimental values for Gd2O3 and Tb2O3.
The investigation of electronic band structure for understanding the electronic and optical properties of X2O3 is very useful. The band structures of the X2O3 were calculated using GGA. The electronic band structures were calculated along the special lines connecting the high-symmetry points Г, H, N, and P for X2O3 in the k-space. The electronic band structure of Gd2O3, and Tb2O3 along the high symmetry directions have been calculated by using the equilibrium lattice constants and are given in Figure 1 and Figure 2.
As can be seen in Figure 1, the Gd2O3 compound has a direct band gap semiconductor with the value 3.86 eV (in Г-high symmetry point). The band gap with the value 3.82 eV of Tb2O3 compound has the same character of that of Gd2O3 (Figure 2). The band gap values obtained for X2O3 are good agreement with the earlier theoretical resuts, but is less than the estimated experimental results [1] [3] [5] . In these figures (Figure 1 and Figure 2), the lowest valance bands that occur between 0 and −3.5 eV (72 energy states) are dominated by O 2p states while the valence bands that occur between −14 eV and −16.5 eV (24 energy states) are dominated by Gd 6s and Tb 6s states. The lowest occupied valance bands are essentially dominated by O 2s (−19 eV and −21.5 eV and include 48 energy states).
3.2. Optical Properties
It is well known that the effect of the electric field vector,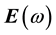 
, of the incoming light is to polarize the material. At the level of a linear response, this polarization can be calculated using the following relation [29] :
![]()
Figure 1. The calculated electronic band structure and Density of State for Gd2O3.
![]()
Figure 2. The calculated electronic band structure Density of State for Tb2O3.
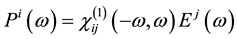(1)
where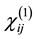 
is the linear optical susceptibility tensor and it is given by [30]
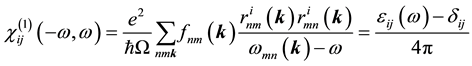(2)
where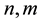 
denote energy bands, 
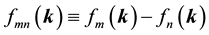is the Fermi occupation factor, 
is the normalization volume.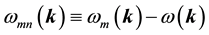 
are the frequency differences, 
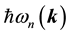is the energy of band n at wave vector
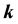. The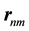 
are the matrix elements of the position operator [30] .
As can be seen in Equation (2), the dielectric function ![]()
and the imaginary part of![]()
, ![]()
is given by
![]()
(3)
The real part of![]()
, ![]()
, can be obtained by using the Kramers-Kroning transformation [30] . Be-
cause the Kohn-Sham equations determine the ground state properties, the unoccupied conduction bands as calculated, have no physical significance.
The known sum rules [30] can be used to determine some quantitative parameters, particularly the effective number of the valence electrons per unit cell![]()
, as well as the effective optical dielectric constant![]()
, which make a contribution to the optical constants of a crystal at the energy![]()
. One can obtain an estimate of the distribution of oscillator strengths for both intraband and interband transitions by computing the ![]()
defined according to
![]()
(4)
where ![]()
is the density of atoms in a crystal, e and m are the charge and mass of the electron, respectively, and ![]()
is the effective number of electrons contributing to optical transitions below an energy of![]()
.
Further information on the role of the core and semi-core bands may be obtained by computing the contribution that the various bands make to the static dielectric constant,![]()
. According to the Kramers-Kronig relations, one has
![]()
(5)
One can therefore define an “effective” dielectric constant, that represents a different mean of the interband transitions from that represented by the sum rule, Equation (5), according to the relation
![]()
(6)
The physical meaning of ![]()
is quite clear: ![]()
is the effective optical dielectric constant governed by the
interband transitions in the energy range from zero to![]()
, i.e. by the polarization of the electron shells.
We first calculated the real and imaginary parts of the linear dielectric function of the Gd2O3, and Tb2O3 compounds (Figure 3 and Figure 4). In order to calculate the optical response by using the calculated band structure, we have chosen a photon energy range of 0 - 65 eV and have seen that a 0 - 40 eV photon energy range is sufficient for most optical functions. We first calculated the real and imaginary parts of linear dielectric function of the Gd2O3 and Tb2O3 compounds (Figure 4 and Figure 5). All the Gd2O3 and Tb2O3 compounds
![]()
Figure 3. The real and imaginary parts of the linear dielectric function and Electron energy-loss spectrum of Gd2O3.
![]()
Figure 4. The real and imaginary parts of the linear dielectric function and Electron energy-loss spectrum of Tb2O3.
studied so far have ε1 are equal to zero in the energy region between 9 eV and 40 eV for decreasing ![]()
and increasing of ![]()
(see, Table 2). Also, values of ![]()
versus photon energy have main peaks in
the energy region 4 eV and 30 eV. Some of the principal features and singularities of the ![]()
for both investigated compounds are shown in Table 3.
The peaks of the correspond to the optical transitions from the valence band to the conduction band and are in agreement with the previous results. The maximum peak values of for Gd2O3 and Tb2O3 are around 9.31 eV and 9.49 eV, respectively.
The corresponding energy-loss functions, ![]()
, were calculated using Equation (7) and are also presented in Figure 3 and Figure 4. The ![]()
describes the energy loss of fast electrons traversing the material. The sharp maxima in the energy loss function are associated with the existence of plasma oscillations [30] . The curves of L have a maximum near 35 eV (Gd2O3) and 38 eV (Tb2O3).
![]()
(7)
The calculated effective number of valence electrons ![]()
is given in Figure 5(a). The effective number of valence electron per unit cell, ![]()
up to 5 eV is zero (below the band gap) then reaches saturation values at
![]()
Figure 5. The calculated (a) effective number of electrons participating in the interband transitions and (b) effective optical dielectric constant.
![]()
Table 2. The energy values at the zero point of real part of dielectric function for Gd2O3 and Tb2O3.
![]()
Table 3. The maximum peak values of the imaginary part of the dielectric function for Gd2O3 and Tb2O3.
about 30 eV (Gd2O3) and 35 eV (Tb2O3). This means that deep-lying valence orbitals participate in the interband transitiond as well (see Figure 1 and Figure 2). The effective optical dielectric constant, ![]()
, is shown in Figure 5(b).
The curves of ![]()
can be arbitrarily divided into two parts. The first part is characterized by a rapid growth of ![]()
and extends up to 12 eV. The second part shows a smoother and slower growth of ![]()
and reaches a saturation values at about 30 eV(Gd2O3) and 35 eV (Tb2O3). This means that the largest contribution to ![]()
is made by transitions corresponding to the bands at ~5 eV and ~12 eV.
4. Conclusion
In the present work, we have made a detailed investigation of the electronic, and frequency-dependent linear optical properties of the X2O3 (X: Gd and Tb) crystals using the density functional methods. The result of the structural optimization implemented using the GGA are in good agreement with the experimental and theoretical results. We have examined photon-energy dependent dielectric functions, some optical properties such as the energy-loss function, the effective number of valance electrons and the effective optical dielectric constants for both materials.
Acknowledgements
This work is supported by the projects DPT-HAMIT, DPT-FOTON, NATO-SET-193 and TUBITAK under Project Nos., 113E331, 109A015, 109E301.
NOTES
*Corresponding author.