Integrity Monitoring in Navigation Systems: Fault Detection and Exclusion RAIM Algorithm Implementation ()
1. Introduction
When Global Positioning System (GPS) is used in those fields where strict performances are required, such as civil aviation, its integrity plays an important role and integrity monitoring functions become necessary. Safety critical applications require consideration of the measure of trust for the position solution derived from the navigation solution. This measure of trust is known as integrity. Users may currently determine their integrity by receiver autonomous integrity monitoring algorithms (RAIM) or by using external integrity data sources such as SBAS [1] . RAIM is the simplest and most cost effective technique for integrity monitoring and quantifies the concept of using a self-consistency check of redundant measurements. The basic concept behind GPS RAIM is the use of additional information to verify position solutions. Since more than the minimum number of four satellites (needed to solve for 3-dimensional position and the clock bias) will be visible in almost all cases, redundant satellite pseudo-range information is available, and the position fix may be computed from a best fit to the over-determined data [2] . The consistency of the redundant measurements provides a clue as to whether a GPS satellite or some other unit is operating out of specification and whether this error makes the position solution unusable. This general approach to RAIM has been developed into various tests of the system geometry and the pseudo-range error residuals which are for the most part functionally equivalent [3] .
The scope of this work is to implement a fault detection and exclusion (FDE) RAIM algorithm in a software GPS receiver and evaluate its performance. The remainder of the paper is organized as follows: Section 2 describes integrity monitoring in navigation systems and RAIM algorithms, focusing in the main methods of implementation. Section 3 gives a detailed description of a baseline FDE algorithm. Then, Section 4 is devoted to our approach in implementing the baseline FDE RAIM algorithm using the parity space method in a GPS software receiver compiled in Matlab® environment. Section 5 presents some test results obtained analyzing the algorithm performance for a set of input data taking into account a static scenario. Finally, Section 6 draws the conclusions of this work.
2. Integrity Monitoring in Navigation Systems
Integrity is often defined as the ability of the navigation system to provide timely warnings to the user when it is inadvisable to use the system for navigation. The GPS system currently provides some basic integrity information to users via the navigation message, but is not timely enough for safety-critical applications [2] . Integrity monitoring in the receiver is essential in safety-critical applications in order to ensure a certain predetermined degree of integrity for the navigation function during some mode of operation. A typical example of an application where integrity monitoring is essential is aviation [4] . However, integrity monitoring techniques are also important in less critical applications to ensure a user position solution with an acceptable quality. RAIM [5] [6] , [7] is a means of providing integrity with the capability of detecting when a satellite failure or a measurement error has occurred. It is based on checking the solution consistency and requires redundant measurements. In three-dimensional positioning where at least four measurements are needed for computing the position and time, fault detection requires at least five measurements and fault exclusion at least six [4] .
Traditionally, RAIM and its performance have mostly been associated with the integrity-monitoring tasks in aviation and other safety-critical applications, where relatively good Line-of-Sight signal reception conditions prevail, and there are often strict rules of well-defined integrity modes. The goal in these traditional RAIM operating environments has been to eliminate large measurement errors due to, for example, satellite clock or ephemeris failures, which can be caused by failures in the satellite or in the control segment. These errors are very rare, with a typical rate of one error per 18 to 24 months in the GPS system [4] . Due to the rarity of these errors, it is usually assumed in traditional RAIM literature that only one erroneous measurement―also called a blunder or an outlier-need to be detected in one measurement epoch. The GPS measurements can also be erroneous for reasons other than control or space segment problems.
A variety of RAIM schemes have been proposed, and all are based on some kind of self-consistency check among the available measurements. In [8] is shown a good example of what is now referred to as a snapshot scheme. With this method, only current redundant measurements are used in the self-consistency check. On the other hand, authors in [9] present a scheme where both past and present measurements, along with a priori assumptions with regard to vehicle motion, are used in the RAIM decision. Such schemes are loosely referred to as averaging or filtering schemes. The snapshot approach has gained more acceptance than the other in recent times because it has the advantage of not having to make any questionable assumptions about how the system got to its present state. It matters only that the system is in a particular state “now”, and the RAIM decision as to failure or no-failure is based on current observations only [2] .
Three RAIM methods have received special attention in recent papers on GPS integrity. These are the following: the range comparison method [8] , the least-squares-residuals method [10] , and the parity method as described in the context of GPS in papers [11] [12] . All three methods are snapshot detection schemes because they assume that noisy redundant range-type measurements are available at a given sample point in time. Also, in all cases, the algebraic problem is linearized about some nominal value of vehicle position and clock bias. The basic measurement relationships are then described by an over-determined system of linear equations of the form:
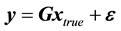 (1)
(1)
where n is the number of redundant measurements;  is the difference between the actual measured range (or pseudorange) and the predicted range based on the nominal user position and the clock bias (
is the difference between the actual measured range (or pseudorange) and the predicted range based on the nominal user position and the clock bias ( is an
is an vector);
vector); 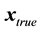 are three components of true position deviation from the nominal position plus the user clock bias deviation (
are three components of true position deviation from the nominal position plus the user clock bias deviation (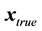 is a
is a 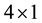 vector); ɛisthe measurement error vector caused by the usual receiver noise, vagaries in propagation, imprecise knowledge of satellite position and satellite clock error, selective availability, and, possibly, unexpected errors caused by a satellite malfunction (ɛ is an
vector); ɛisthe measurement error vector caused by the usual receiver noise, vagaries in propagation, imprecise knowledge of satellite position and satellite clock error, selective availability, and, possibly, unexpected errors caused by a satellite malfunction (ɛ is an 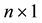 vector); and
vector); and 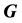 is the usual linear connection matrix arrived at by linearizing about the nominal user position and clock bias. (
is the usual linear connection matrix arrived at by linearizing about the nominal user position and clock bias. (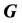 is an
is an 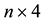 matrix.)
matrix.)
3. Fault Detection and Exclusion Algorithm
In this section, the fault detection and the exclusion RAIM algorithmare described [5] . The linearized relation between changes in the measurements and the corresponding change in the user state vector is given by:
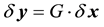 (2)
(2)
where is a
is a  vector containing the changes in the measurements to m sources,
vector containing the changes in the measurements to m sources,  is the change in the
is the change in the 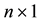 user state vector, and
user state vector, and ![]() isa
isa ![]() data matrix. The data matrix
data matrix. The data matrix ![]() can be decomposed into the product of a real orthonormal matrix Q and an upper triangular matrix R using “QR” factorization [13] . Substituting (2) into the decomposed matrix
can be decomposed into the product of a real orthonormal matrix Q and an upper triangular matrix R using “QR” factorization [13] . Substituting (2) into the decomposed matrix ![]() and pre-multiplying both sides by
and pre-multiplying both sides by ![]() yelds
yelds![]()
![]() (3)
(3)
The rank of R is equal to the rank of G; therefore, the lower ![]() rows of R consist of zeros only. Equation (3) can be divided into two equations
rows of R consist of zeros only. Equation (3) can be divided into two equations
![]() (4)
(4)
and
![]() (5)
(5)
whereU consists of the first n rows of R, ![]() consists of the first n rows of
consists of the first n rows of ![]() , and
, and ![]() consists of the last
consists of the last ![]() rows of
rows of![]() . Equation (4) relates the change in the measurements to the change in the user state vector, forming the least square solution [5] . The rows of
. Equation (4) relates the change in the measurements to the change in the user state vector, forming the least square solution [5] . The rows of ![]() and
and ![]() are orthogonal; therefore, the columns of
are orthogonal; therefore, the columns of ![]() span the parity space of
span the parity space of![]() . If the measurements are corrupted by errors, then
. If the measurements are corrupted by errors, then![]() is replaced by
is replaced by![]() where
where ![]() is a
is a![]() vector representing zero-mean, normally distributed measurement noise, and
vector representing zero-mean, normally distributed measurement noise, and ![]() is a
is a![]() vector containing bias errors. Normally,
vector containing bias errors. Normally,![]() and
and ![]() are unknown, but their components in parity space are known from Equation (6).
are unknown, but their components in parity space are known from Equation (6).
![]() (6)
(6)
The expected value of the parity vector,![]() , is given by (7)
, is given by (7)
![]() (7)
(7)
The covariance matrix of![]() is given by (8).
is given by (8).
![]() (8)
(8)
If the measurement noise is uncorrelated and normally distributed with equal variances, then the covariance matrix of the measurement noise is
![]() (9)
(9)
whereIis a![]() identity matrix. It then follows that the covariance matrix of
identity matrix. It then follows that the covariance matrix of![]() is
is
![]() (10)
(10)
since![]() (the rows of
(the rows of ![]() are orthonormal vectors). In the absence of bias errors, the parity vector
are orthonormal vectors). In the absence of bias errors, the parity vector![]() is a function of measurement noise only. In the presence of bias errors,
is a function of measurement noise only. In the presence of bias errors,![]() also depends on the bias errors. The detection rule states that the failed satellite is the one whose characteristic bias error line in the parity space lies along the observed parity vector
also depends on the bias errors. The detection rule states that the failed satellite is the one whose characteristic bias error line in the parity space lies along the observed parity vector![]() [5] .
[5] .
4. Algorithm Implementation in a GPS Software Receiver
In this section, we describe our approach in integrating the baseline fault detection and exclusion RAIM algorithm [5] into a GPS software receiver compiled in Matlab® environment. This analysis deals with the simplest method to provide integrity using a GPS system in combination with autonomous user integrity algorithms. In presence of a failure, the RAIM algorithm should be able to raise an alarm in order to warn the user that the computed position is not safe for the specific application. This is done by properly setting the protection level and the test statistic [14] . A RAIM algorithm is designed to satisfy the required probability of missed detection, therefore a certain number of missed detections are allowed. The algorithm baseline is given inFigure 1.The implementation diagram is build up of two main blocks: the first one is the navigation engine which belongs to the GPS software receiver compiled in Matlab® which has the duty to compute the user’s position, velocity and time from the raw measurements. In order to check the consistency of the solution a second block is added; the baseline FDE RAIM algorithm.This block takes as input from the navigation engine the matrix of unit line-of-sight vectors from user to satellites and the standard deviation of measurement noise (σ), while from the specific requirements, are fed into the algorithm the probability of false alarm (Pfa) and probability of missed detection (Pmd).
Next, the algorithm computes the protection levels (PL) and detection thresholds and based on statistic decision theory it builds a test statistic based on the parity space method, which is then compared with the threshold [3] . After that the algorithm gives as output the state of the solution which is described in more details in the flow-chart ofFigure 2.
In the first phase of the implementation our interest is on detecting unconsistent solutions. The output states of the algorithm are five. First, if enough redundant measurements are present (at least five measurements) the test statistic is compared with the precomputed detection threshold. If the test statistic exceeds the value of the threshold, then is compared the value of the position error (PE) with the protection level and if it is the case that the position error is higher than the protection level the true alarm flag is raised, warning the user to not use the navigation system. On the other hand if the test statistic exceeds the threshold but the value of the position error is less than the protection level a false alarm is raised. The navigation system is working under normal operation conditions if the test statistic doesn’t exceed the detection threshold and the position error is bounded by the protection level. The missed detection flag is raised in the case when the test statistic is less than the threshold but the position error exceeds the value of the protection level. In the case where redundant measurements are not enough, the RAIM algorithmcannot properly work and it will set as output the unavailability flag which
![]()
Figure 1.Implementation diagram of the baseline FDE RAIM algorithm in a GPS software receiver.
![]()
Figure 2.GPS and RAIM algorithm flow-chart.
means that the consistency of the solution cannot be checked.
In the second phase, rather than performing fault detection, isolation and reconfiguration, the algorithm only requires exclusion of the malfunctioning signal. All that the receiver must do is to use a set of redundant measurements that does not raise the alarm. For example, if satellite 6 malfunctions, then this satellite must be excluded from the navigation solution. No action is necessary if satellite 6 was not part of the navigation solution. The basic idea of FDE can be illustrated with an eight-in-view example. Suppose that the normal detection suite operates with only six satellites, as suggested in [11] , and an alarm occurs. Instead of immediately trying to isolate the bad satellite, the FDE algorithm simply searches among all the other six-satellite subsets for one that will satisfy its self-consistency test, thus assuring that the bad satellite has been excluded. InFigure 3, the iterative fault exclusion algorithm is shown. In case the estimation problem is overdetermined (i.e., when there are more independent measurements than unknowns), the GPS measurements are said to be redundant.
Since the measurements are affected by noise and other errors, the measurement vector will not fit exactly the Weighted Least Squares (WLS) solution, and there will be some pseudorange residuals left. These residuals are defined as the difference between the estimated values of the observations and their corresponding measured values [4] . Assuming that the measurement model is correct, the observational residuals indicate the extent to which the measurements agree with each other. The process of outlier detection starts by first performing a global test to detect the presence of outliers, and then a local test to identify the largest outlier which is then rejected. The process may be iterated for several outliers.
The global test for assessing whether the set of measurements includes errors or not is performed by calculating first a test statistic (TS). To execute the test, we need the critical value of the test. This is the threshold against which the test parameter is compared. Pfa = 0.1 and Pmd = 0.2 are used. If TS exceeds the threshold, an inconsistency is assumed and the local test is performed to identify which measurement is the cause of the inconsistency. In the case of the global test, the null hypothesis H0 states that the model is correct and the measurement errors are normally distributed and there are no bias errors in the set of measurements. The alternative hypothesis Ha states that the model is wrong, or that the assumption is not correct, which means that there are at least some bias errors in the set of measurements and the errors are not zero-mean normally distributed.
The assumption is that the measurement set contains at most one erroneous measurement. Therefore the local test is done only when the global test fails (i.e., has indicated the presence of an outlier). If the local test detects an erroneous measurement, then this measurement is rejected and the remaining measurements are used to calculate the solution. If the global test fails, but the local test does not indicate an erroneous measurement in the observation set, the solution is concluded to be unreliable. In the case of the local test, the null hypothesis of no error, is denoted by H0,k and the alternative hypothesis of a biased measurement, Ha,k[4] .
5. Results and Discussions
In this section, we provide the results of our work. Exhaustive testing of the integrity algorithm requires a large amount of calculations, e.g. to verify the horizontal radial position error, a minimum of 1011 simulations are required [5] . Fortunately, because of the Gaussian statistics of the algorithm described above, it is possible to test
![]()
Figure 3.Iterative fault exclusion algorithm.
the algorithm using increased measurement errors. To test the implemented RAIM algorithm the strategy of increased measurement errors is followed. A set of collected GPS raw measurements of around 7 minutes, in a static scenario is taken into consideration. Below are described two cases of testing: the first is the one with normally distributed measurement errors, while in the second the approach of increased measurement errors is used in order to observe the effect in the output states of the RAIM algorithm and its ability to detect failures.
In Figure 4is given the relation between the output states of the RAIM algorithm with respect to time. The navigation engine of GPS software receiver processes new measurements every second (position computation rate), and after that an output is provided from the RAIM algorithm. As it is shown in Figure 4, during all the time the output state of the algorithm is “normal operation”, which means that enough redundant measurements (in our case six satellites are in fix) are present, the integrity requirements for the mode of operation are met and the provided position solution is reliable.
Figure 5 shows the results of the second case where we increase the generated measurement noise by properly increasing the standard deviation of measurements noise. It can be see that 394 times the output state of the algorithm is set to “false alarm” which means that the test statistic is higher than the detection threshold but the value of the position error is less than the protection level. The number of the cases that a “true alarm” is raised is 7, which means that a failure is detected because the test statistic exceeds the value of the threshold and the position error is higher than the protection level, so the positioning solution is not reliable and the system should not be used for the intended mode of operation. The output flag is set only once in the “missed detection” state which means that the test statistic is less than the threshold but the position error exceeds the value of the protection level. The number of “normal operation” cases is 26 which means that the test statistic doesn’t exceed the detection threshold and the position error is within the protection level, so the solution is consistent. Note that the “unavailable” output state is never set since enough redundant measurements (more than 4 satellites in view) are always present. By comparing the above cases one can observe that in the nominal case the collected data are good and the geometry is admissible, while with the increased measurement errors the algorithm detects failures and properly raises the alarms indicating the user to not use the navigation system.
Figure 6shows the WLS position result for the given measurement data in a local coordinate frame (north-east) when all the available measurements are used, and highlights the positions that have been detected to be erroneous by the global test. The script outputs the measurements detected as outliers by indicating the faulty satellite.Figure 7presents the positioning result when these faulty observations have been excluded from the WLS solution. For a quantitative understanding, the horizontal error results are shown inTable 1. In the case the FDE RAIM algorithm is applied, the maximum horizontal error is reduced almost by a factor of 18 which illustrates the significant improvement in positioning accuracy.
6. Conclusion
In this paper, a review on RAIM algorithms was provided. A baseline fault detection and exclusion RAIM algorithm was implemented in a GPS software receiver using the parity space method. For algorithm testing a static
![]()
Figure 4.The output states of the RAIM algorithm versus time for normal measurement errors.
![]()
Figure 5.The output states of the RAIM algorithm versus time for increased measurement errors.
![]()
Figure 6.The WLS positioning result with all available measurements.
![]()
Figure 7.The WLS positioning result when fault detection and exclusion is applied.
![]()
Table 1.Horizontal error results for the positioning solution.
scenario was considered where the collected data were processed to check the consistency of the provided solution. During all the time, enough redundant measurements were available. Two scenarios were used to test the algorithm, the first one with zero-mean normally distributed measurement errors and the second one with increased measurement errors. The results show that the algorithm performs well by properly detecting faults in the second scenario compared with the first one where the system is in normal operation. After applying the iterative fault exclusion algorithm, a significant improvement in positioning accuracy is achieved. The FDE algorithm is able to identify and exclude the satellite of the GPS constellation, if affected by a bias before the position error exceeds the required protection levels.
NOTES
*Corresponding author.