A Simple Proof of Gustafsson’s Conjecture in Case of Poisson Equation on Rectangular Domains

Gangjoon Yoon¹, Chohong Min²

¹Institute of Mathematical Sciences, Ewha Womans University, Seoul, South Korea.
²Department of Mathematics, Ewha Womans University, Seoul, South Korea.

DOI: 10.4236/ajcm.2015.52005                

Abstract

We consider the standard five-point finite difference method for solving the Poisson equation with the Dirichlet boundary condition. Its associated matrix is a typical ill-conditioned matrix whose size of the condition number is as big as . Among ILU, SGS, modified ILU (MILU) and other ILU-type preconditioners, Gustafson shows that only MILU achieves an enhancement of the condition number in different order as . His seminal work, however, is not for the MILU but for a perturbed version of MILU and he observes that without the perurbation, it seems to reach the same result in practice. In this work, we give a simple proof of Gustafsson's conjecture on the unnecessity of perturbation in case of Poisson equation on rectangular domains. Using the Cuthill-Mckee ordering, we simplify the recursive equation in two dimensional grid nodes into a recursive one in the level that is one-dimensional. Due to the simplification, our proof is easy to follow and very short.

Keywords

Five-Point Finite Difference Method, Modified ILU Preconditioning, Condition Number

1. Introduction

Consider the standard five-point finite difference method for solving the Poisson equation with the Dirichlet boundary condition. Its associated matrix is a typical ill-conditioned matrix whose condition number is of size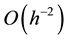, where h is the grid size. In mitigating the large size, Dupont, Kendall and Rachfold [1] propose a preconditioning technique which works quite well for elliptic problems with 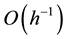convergence rate, which is a simple modification of incomplete LU (ILU) and called the modified ILU (MILU) preconditioning techni- que. The MILU requires all the same row sums for the preconditioner and the original matrices. Also, Gusta- fsson [2] [3] shows that the MILU preconditiong reduces the size to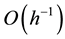, while other popular precon- ditionings such as ILU and symmetric Gauss-Seidel (SGS) do not improve the order. Numerical study by Greenbaum and Rodrigue [4] indicates that further reduction is not possible with the same sparsity pattern.

The MILU preconditioing introduced by Axelsson [5] and developed by Gustafsson [2] adds some artificial diagonal perturbation on the orginal matrix. In [1] and [2] , it is found that a small positive perturbation improves the convergence rate quite well for many elliptic problems. We refer to [6] -[9] and references therein for more results and details.

The numerical experiments [10] with Dirichlet boundary condition, however, suggest that the perturbation is unnecessary. It is Gustafsson’s conjecture [2] [11] to prove the estimate for the unperturbed MILU preconditioing. Beauwens [12] considers a general setting that includes the five-point method, and proves the conjecture using the matrix-graph connectivity properties (see also [13] ). Beauwens’ proof deals with a Stieltjes matrix under several assumptions. Notay [14] also obtains an upper bound 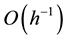for the block MILU with the line partitioning. We also refer the reader to [15] -[18] for related works on Gustafsson’s conjecture.

We introduce a novel and heuristic proof for the conjecture in case of Poisson equation with Dirichlet boundary condition on rectangular domains. The MILU preconditioner is obtained from recursively calculating the row-sum equation at each grid node in the lexicographical ordering. In the case of the five-point method, it is well known [19] that the same matrix can be obtained in the Cuthill-Mckee ordering. The matrix entry on the

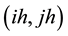node depends only on 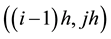and 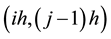nodes, both of which lie on the same level 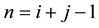of the Cuthill-Mckee ordering. So we can simplify the recursive equation in two dimensional grid

nodes into a recursive one in the level that is one dimensional. Due to the simplification, our proof is easy to follow and very short.

2. MILU Preconditioning

Consider the Poisson equation 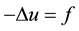in a rectangular domain 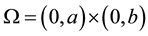with the Dirichlet boun- dary conditi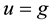on on. The standard five-point finite difference method approximates the equation as

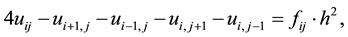
at each grid node. The approximations constitute a linear system. With the lexicographical ordering, we decompose the matrix as

where L, U, and D are its strictly lower and upper, and diagonal parts, respectively. MILU preconditioner is the matrix of the form, where the diagonal matrix E is obtained recursively as follows.

for

for

Here denotes the diagonal element of E corresponding to the node point, i.e.. and denote the entry and, respectively. Note that the above formula results from

the row sum property, with. Due to the Dirichlet boundary condition, and are either or 0, and.

Lemma 1. Let be a sequence defined recursively as

(1)

Then we have

Proof. Let be the sequence defined as (1). The lemma is shown by the mathematical induction. Assume that for Then

and this proves the lemma.

Theorem 1. Let be the MILU preconditioner for A. Then, for every diagonal element of E corresponding to the node, we have

and, therefore,

Proof. We shall show that for by mathematical induction on. Then follows the result from the previous lemma. When,. Assume that for all with. Then for any with,

Now, we are ready to estimate the condition number of the MILU preconditioned matrix. The fol- lowing analysis is a standard approach, for the details see [2] . Since is similar to

that is symmetric and positive definite, all the eigenvalues of are real and positive. Moreover, the minimum and maximum eigenvalues of are given as

(2)

and is written in the form

(3)

for the matrix (see (b) of Figure 1 for its entries). For arbitrary, we have

(4)

(a) (b)

Figure 1. Matrices A and R. (a) Matrix A; (b) Matrix B = M ? A.

Using the inequality and Theorem 1, we also have

Thus, we obtain the inequalities

(5)

In summary, we have the following.

Theorem 2. Let be an eigenvalue of the MILU preconditioned matrix, then and

(6)

Proof. Let be an eigenvalue of the MILU preconditioned matrix From (5), we have that

and applying these inequalities above into (2) and (3) gives

which shows the inequalites (6). On the other hand, the row sum property implies that 1 is an eigenvalue of. Thus, we have and we complete the proof.

Corollary 1. The ratio of the maximum and minimum eigenvalues of the MILU preconditioned matrix is bounded by.

Remark 1. Our analysis deals with the two dimensional Poisson equation. It naturally extends to the three dimensional equation in a dimension-by-dimension manner.

Acknowledgments

This work was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (2009-0093827).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dupont, T., Kendall, R. and Rachford, H. (1968) An Approximate Factorization Procedure for Solving Self-Adjoint Elliptic Difference Equations. SIAM Journal on Numerical Analysis, 5, 559-573. http://dx.doi.org/10.1137/0705045
[2]	Gustafsson, I. (1978) A Class of First Order Factorization Methods. BIT Numerical Mathematics, 18, 142-156. http://dx.doi.org/10.1007/BF01931691
[3]	Greenbaum, A. (1997) Iterative Methods for Solving Linear Systems. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970937
[4]	Greenbaum, A. and Rodrigue, G.H. (1989) Optimal Preconditioners of a Given Sparsity Pattern. BIT Numerical Mathematics, 29, 610-634. http://dx.doi.org/10.1007/BF01932737
[5]	Axelsson, O. (1972) A Generalized SSOR Method. BIT Numerical Mathematics, 13, 443-467. http://dx.doi.org/10.1007/BF01932955
[6]	Axelsson, O. (1994) Iterative Solution Methods. Cambridge University Press, Cambridge.
[7]	Chan, T.F. and van der Vorst, H.A. (1997) Approximate and Incomplete Factorizations. In: Keyes, D.E., Sameh, A. and Venkatakrishnan, V., Eds., Parallel Numerical Algorithms, ICASE/LaRC Interdisciplinary Series in Science and Engineering, 4, Kluwer Academic, Dordrecht, 167-202.
[8]	Hackbusch, W. (1994) Iterative Solution of Large Sparse Linear Systems of Equations. Applied Math. Sci. Series, No 95, Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-4288-8
[9]	Notay, Y. (1992) Upper Eigenvalue Bounds and Related Modified Incomplete Factorization Strategies. In: Beauwens, R. and de Groen, P., Eds., Iterative Methods in Linear Algebra, Amsterdam, North-Holland, 551-562.
[10]	Bruaset, A.M. and Tveito, A. (1992) RILU Preconditioning; A Computational Study. Journal of Computational and Applied Mathematics, 39, 259-275. http://dx.doi.org/10.1016/0377-0427(92)90203-A
[11]	Gustafsson, I. (1979) Stability and Rate of Convergence of Modified Incomplete Cholesky Factorization Method. Research Report 79.02R, Department of Computer Sciences, Chalmers University of Technology and University of Göteborg, Göteborg, Sweden.
[12]	Beauwens, R. (1984) Upper Eigenvalue Bounds for Pencils of Matrices. Linear Algebra and Its Applications, 62, 87-104. http://dx.doi.org/10.1016/0024-3795(84)90088-0
[13]	Beauwens, R. (1985) On Axelsson’s Perturbations. Linear Algebra and Its Applications, 68, 221-242. http://dx.doi.org/10.1016/0024-3795(85)90214-9
[14]	Notay, Y. (1991) Conditioning Analysis of Modified Block Incomplete Factorizations. Linear Algebra and Its Applications, 154-156, 711-722. http://dx.doi.org/10.1016/0024-3795(91)90400-Q
[15]	Axelsson, O. and Eijkhout, V. (1987) Robust Vectorizable Preconditioners for Three-Dimensional Elliptic Difference Equations with Anisotropy. In: te Riele, H.J.J., Dekker, Th.J. and van der Vorst, H.A., Eds., Algorithm and Applications on Vector and Parallel Computers, North-Holland Publishing Co., Amsterdam, 279-306.
[16]	Axelsson, O. (1989) On the Eigenvalue Distribution of Relaxed Incomplete Factorization Methods and the Rate of Convergence of Conjugate Gradient Methods. Technical Report, Department of Mathematics, Catholic University, Nijmegen, The Netherland.
[17]	Beauwens, R., Notay, Y. and Tombuyses, B. (1994) S/P images of Upper Triangular M-Matrices. Numerical Linear Algebra with Applications, 1, 19-31. http://dx.doi.org/10.1002/nla.1680010104
[18]	Notay, Y. (1991) Conditioning of Stieltjes Matrices by S/P Consistently Ordered Approximate Factorizations. Applied Numerical Mathematics, 10, 381-396. http://dx.doi.org/10.1016/0168-9274(92)90058-L
[19]	Min, C. and Gibou, F. (2012) On the Performance of a Simple Parallel Implementation of the ILU-PCG for the Poisson Equation on Irregular Domains. Journal of Computational Physics, 231, 4531-4536. http://dx.doi.org/10.1016/j.jcp.2012.02.023