Quantum Inspired Differential Evolution Algorithm

Binxu Li, Panchi Li

School of Computer and Information Technology, Northeast Petroleum University, Daqing, China.

DOI: 10.4236/ojop.2015.42004                

Abstract

To enhance the optimization performance of differential evolution algorithm, by studying the implementation mechanism of differential evolution algorithm, a new idea of incorporating differential strategy and rotation of qubits in the Bloch sphere is proposed in this paper. In the proposed approach, the individuals are encoded by qubits described on Bloch sphere, and the rotation angles of qubits in current individual are obtained by differential strategy. The axis of rotation is designed by using vector product theory, and the rotation matrixes are constructed by using Pauli matrixes. Taking the corresponding qubits in current best individual as targets, the qubits in current individual are rotated to the target qubits about the rotation axis on the Bloch sphere. The Hadamard gates are used to mutate individuals. The simulation results of optimizing the minimum value of functions indicate that, for an iterative step, the average time of the proposed approach is 13 times as long as that of the classical differential evolution algorithm. When the same limited steps are applied in two approaches, the average optimization result of the proposed approach is 0.3 times as great as that of the classical differential evolution algorithm; when the same running time is applied in two approaches, the average optimization result of the proposed approach is 0.4 times as great as that of the classical differential evolution algorithm. These results suggest that the proposed approach is inefficient in computational ability; however, it is obviously efficient in optimization ability, and the overall optimization performance is better than that of the classical differential evolution algorithm.

Keywords

Quantum Computation, Qubits Encoding, Bloch Spherical Search, Quantum Differential Evolution

1. Introduction

Differential evolution algorithm is a bionic intelligent optimization method proposed by American scholar Storn and Price in 1995. This algorithm simulated the “survival of the fittest” natural evolution law. In 2004, Price and others published the first monograph of the algorithm, which has become a classic in the field of DE algorithm [1] . In 2008, Chakraborty published his work named “Advances in Differential Evolution” [2] , in which he made a comprehensive and systematic explanation to the theory, the application and the developing direction in the future of DE. In order to improve the optimization ability of DE algorithm, speed up the convergence and overcome the premature convergence phenomenon of the common heuristic algorithm, many scholars made improvements on DE algorithm. Ref. [3] proposed a crossover mutation differential evolution algorithm. This method firstly divided the species into two groups according to the fitness, and then selected individuals from two groups respectively and implemented intersection between groups, which could ensure the species had higher diversity. Ref. [4] proposed a self-adaption species adjustment scheme. This method can delete redundant individuals automatically according to the current state of search, which improved the ability of search. Ref. [5] proposed a method which adjusted the scale factor and the crossover possibility respectively by the Gaussian distribution and the uniform distribution, so that the diversity of the species could be improved. Considering about the impact of population initialization algorithm for optimizing performance, Ref. [6] proposed a new method of the species initialization which was based on quadratic interpolation and nonlinear simplex. In terms of integration with other algorithms, Ref. [7] proposed a self-adaption memetic differential evolution algorithm. Ref. [8] proposed a kind of differential evolution algorithm which was fused with genetic algorithm and applied to the Doppler source of radiation research. The crossover operator used in the classical differential evolution algorithm has a flaw, that is to say, it can only generate one vertex of the super rectangle solid. To address this problem, Ref. [9] proposed a new kind of orthogonal crossover operator. This operator can search more effectively in the matrix defined area. Now most majorities of differential evolution algorithms are appropriated for the continuous optimization. For combinatorial optimization, converting real solutions into integer solutions by decoding method is the common way. For this problem, Ref. [10] proposed a differential evolution algorithm based on integer (or discrete) coding. This algorithm effectively improved the optimization efficiency of dealing with the discrete matters by differential evolution algorithm. To enhance the convergence speed of the algorithm, Ref. [11] [12] proposed a new mutation strategy which differed the optimal and the worst individuals at the beginning of the algorithm. This method not only effectively balanced the exploration and the development of the algorithm, but also enhanced the ability to detect the solution space. Ref. [13] studied the distributed differential evolution model, and also proposed two new species of migration strategies. These improvements improved the optimization ability of differential evolution algorithm in some extent.

Quantum computing is a new computing model derived from quantum mechanics. At present, in the aspect of integrating particle swarm optimization, the basic theory and the applied research are mature. Sun Jun simulated the particles’ movement to the lowest energy point in the quantum potential well, by which they firstly put forward quantum behavior particle swarm algorithm [14] . The core problem of quantum-inspired genetic algorithm is how to design the coding scheme and the evolutionary operators. Currently the most commonly used method of the qubit coding is the one based on the description of the unit circle. The two probability amplitudes of the qubit are both real number, in which there is only one adjustable phase parameter. In regard to the evolutionary operator, the usual way is to change the quantum rotation gate and the quantum NOT-gate with only one phase parameter. However, the real qubit is based on the description of the Bloch sphere, not only the two probability amplitudes of which are complex numbers. It also includes two phase operators. Ref. [15] presented an individual coding method that adopted qubit Bloch coordinate. Even though this method strengthened the characteristics of the quantum, it still overlooked the matching relationship between two parameters’ adjustment amount. From the point of the geometry, the bits on the Bloch sphere cannot move to the target bit along the shortest path, so that the optimization ability is limited. Thus, how to design a new kind of coding method and evolutionary operator to enhance the optimization ability of the quantum-inspired evolutionary algorithm is a project deserving further study.

Based on the above consideration, this article selected the differential evolution algorithm as the entry point, and presented the Bloch quantum-inspired differential evolution algorithm, which is called BQDE for short. This algorithm used the qubit described by the Bloch sphere (not its Bloch coordinate) to encode the individuals directly, used the qubit vector product to build the rotation axis, and used the quantum computing principle to construct the rotation matrix. On the Bloch sphere, it realized the individual’s evolution by the qubit’s pivoting, and used Hadamard gate to achieve individual’s evolution to increase the diversity of the species. This method can simultaneously adjust two parameters of the qubit in the best matching mode. Taking typical function extremum for example, the simulation result shows that the optimization ability of this algorithm is obviously better than that of the common differential evolution algorithm.

The remainder of the paper is structured as follows. Section 2 gives a brief survey on Common Differential Evolution (CDE) Algorithm. Section 3 describes the basic principle of BQDE algorithm. In Section 4, we test our algorithm using 8 benchmark functions and also compare our results with CDE. Section 5 contains the conclusions.

2. Differential Evolution Algorithm

Let NP denote the population size, D denote the dimension of the feasible solution space, and 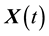denote the

population in the t^th generation. The initial population is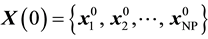, where.

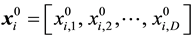2.1. Mutation Operation

For any target vector in the parent population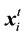, differential evolution algorithm can generate the mutation vector 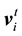as follows [16] .

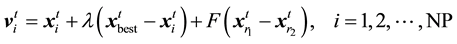, (1)

where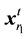, 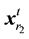denote individuals selected randomly in the parent generation.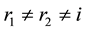, , 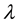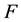denote the scaling factors.

2.2. Crossover Operation

Differential evolution algorithm (DE) generated the new crossover vector 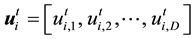by restructuring every dimension component of the mutation vector 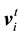and the target vector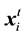. The definite crossover method is as follows:

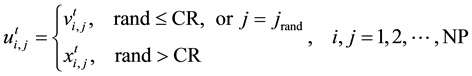, (2)

where rand is the random number between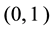.. CR is the constant between.

2.3. Selecting Operation

Differential evolution algorithm adopted the greedy choice strategy. The new individual can only be accepted when it is superior to. Otherwise, would be kept in the next generation of population. Let denote the optimization question. The selecting operation is shown as follows.

, (3)

By the selecting operation, differential evolution algorithm makes the individuals in the child population are always better than that in the parent population. This can make the population always evolve in the direction of the optimal solution.

3. The Basic Principle of BQDE Algorithm

3.1. The Qubit Description Based on Bloch Sphere

In the quantum computation, qubit has two ground states: and. According to the principle of superposition, qubit can be expressed by the linear combination of the two ground states.

, (4)

where,.

Since and is continuous, so that one qubit can describe infinite different states. A qubit can be described by a point on the Bloch sphere. As is shown in Figure 1, where, ,. Thus, the qubit can also be described by the vector in two-dimensional complex Hilbert space as follows.

. (5)

Now every point on the Bloch sphere is corresponds to a qubit.

3.2. Encoding Method of BQFE

BQDE algorithm encodes individuals by the qubits described based on the Bloch sphere. Let NP denote the population size, D denote the dimension of optimization space, and denote the t-th generation population. And then the i-th individual can be coded (initialized) as follows.

, (6)

where, ,.

3.3. Measure of Qubit

According to the principles of Quantum computing, we can acquire the Bloch coordinate of by the Pauli matrices. This process is called the projection measurement of qubit. The definition of Pauli matrices are shown as follows.

. (7)

The projection measurement calculation formula of qubit is below.

(8)

Figure 1. A qubit description on the Bloch sphere.

. (9)

. (10)

3.4. Solution Space Transformation

In BQDE, three optimal solutions made by each individual were expressed by Bloch coordinates. Since the Bloch coordinates, we have to transform the optimal solutions to the actual problem solution space. Set the j-th variable, the solution space transformation can be described as follows.

, (11)

, (12)

, (13)

where,.

3.5. Individual Evolution of BQDE

In BQDE, we will establish the searching mechanism relay on the Bloch sphere, which can make the qubit revolve around a certain axis towards the target bit. Set t-th generation’s optimal individual as. For the i-th individual, we firstly choose two individuals randomly, , , and then let

denote the angle between and, and denote the angle between

and. For, the rotation angle can be obtained as the follows.

, (14)

where denote scale factors.

Taking on as target, rotate the on through about axis towards

to, and thus the individual’s evolution of has accomplished.

3.5.1 . Determination of the Rotation Axis

In order to rotate towards, the selection of the rotate axis is crucial. Based on the theory of Hilbert space vector produce, we present the following method.

On the Bloch sphere, set and, which respectively correspond the point and. The axis of rotating the qubits from point towards to point is.

Set the Bloch coordinates of and as and.

According to the method above, the axis of rotating towards is defined as follows.

, (15)

where,.

3.5.2 . Determination of the Rotation Matrix

According to the quantum computing principle, the rotation matrix made the qubit revolve about the unit vector axis with a angle on the Bloch sphere is below.

, (16)

where denote an unit matrix,

Thus, on the Bloch sphere, the rotation matrix that made the current bit revolve around the axis towards to is given as follows.

, (17)

The rotate operation made the current bit revolve towards to the target bit is below.

, (18)

where, , denotes the iteration step.

3.5.3 . Crossover Operation of BQDE

BQDE adopted the same crossover strategy as CDE does. With help of the recombination of the qubit before and after the individual’s evolution, the new crossover individual was generated. Where

, (19)

where rand is the random between, CR is the constant between.

3.5.4 . Selected Operation of BQDE

BQDE adopted the same selection strategy with CDE, which is the Greedy Selection Mode. The new individual can be accepted if and only if it’s superior to than. Otherwise would be kept into the next generation. Set and after the projection measurement and the solution space transformation respectively corresponds to and, the operation can be described as follows.

, (20)

where.

4. Experimental Result Contrasts

4.1. Test Functions

Use the following eight standard test functions to verify the performance of BQDE, and compared with CDE. All eight functions are minimum optimization, which denotes the minimum extreme value point. All test functions are standard, unconstrained, single objective benchmark functions with different characteristics. For example, the is multi-modal, non-separable, and has a very narrow valley from local optimum to global optimum. The and are multi-modal, non-separable, asymmetrical, local optima’s number is huge. The is multi-modal, non-separable, asymmetrical, continuous but differentiable only on a set of points.

(1), ,.

(2), ,.

(3), ,.

(4), ,.

(5), ,.

(6), , ,.

(7), , , .

(8)., , , ,.

4.2. Some Definitions

Precision threshold: when the preset Maximum Iterative Steps (MIS) reaches, if, the algorithm is convergence, otherwise it is not convergence.

Error E: the error definition of a optimized solution is defined as.

Iterative steps (IS): the iterative steps when the algorithm reaches convergence. If the algorithm is not convergence, set IS = MIS.

Running time (RT): the average time of executing an iteration.

4.3. Parameter Setting

In the CDE algorithms, the range of the scale factor and the crossover probability. To determine the most reasonable combination of the three parameters above, we firstly select, CR from, which can compose 1000 kinds of combination. Then taking 30-dimension function as example, each combination was optimized 50 times by CDE, and each iteration steps are 1000. Finally by comparing the average value of the 50 times optimal results, when, is equal to 0.6 and CR is equal to 0.8, the optimization is the best. Thus, in the following experiments, we set and for BQDE and CDE.

Considering the large amount of calculation of the BQDE, we found that the running time of which are about 10 to 20 times to CDE after a lot of simulations. To enhance the credibility of the performance of BQDE, it is necessary to make comparison in the same period of time. Thus, the maximum iteration step is MIS = 10⁴ for BQDE, and is MIS = 10⁴ and MIS = for CDE.

The other parameter settings of two algorithms are as follows: Population size; Function dimension; Precision threshold: for, , ,; for and,; for,; for,; for,.

To reflect the superiority of the proposed algorithm and deduce the randomness of it, each function would be optimized 50 times independently by BQDE and CDE. Choose the following items from the 50 optimization results as the comparison index. These items are as follows: the Mean and the standard deviation (STD) of the error E, the Mean and the standard deviation (STD) of the iteration steps, the number of convergence (NC) and the running time (RT).

4.4. Results Comparison and Analysis

The two algorithms were implemented on the computer with 2.0 GHz CPU and 1.0 G RAM, using Matlab7.0 simulation software. The result contrasts of the average error, the standard deviation of error, the number of convergence, and the running time are shown in Table 1. The comparison of the average and the standard deviation of the iteration steps are shown in Table 2.

The experimental results show that for the contrast of every index, BQDE is obviously superior to CDE not

Table 1. The mean and standard deviation contrasts of error E for 50 trials.

Table 2. The mean and standard deviation contrasts of iterative steps IS for 50 trials.

only when the iteration steps of two algorithms are the same, but also when the optimization times of two are same. For the experimental results above, we can analysis as follows.

First, BQDE adopted the same DE strategy with CDE so that it obtains the advantages CDE. Second, BQDE coding scheme shows that every individual can give three optimal solutions simultaneously. And the three optimal solutions would be updated with each iteration step. This effectively enhanced the ergodicity of solution space. Third, BQDE adopted a qubit update method that the qubit rotate on the Bloch sphere about an axis. These methods not only can adjust the two parameters of qubits simultaneously, but also can achieve the best match between the two parameters so that to enhance the efficiency of optimization. Besides, it’s worth pointing out, the computing efficiency of BQDE is pretty low since BQDE involves many matrix operations (such as construct the axis of rotation, revolve operation, projection measurement). As the experiment results show, BQDE’s running time is 10 to 20 times of CDE’s. According to the No Free Lunch Theorem, BQDE gained the performance improvement in expense of scarifying the computing efficiency. BQDE is also obviously better than CDE when comparing with the same period of time (at this time, CDE’s iteration steps is 20 times of BQDE’s). These experimental results show that the CDE’s performance cannot be apparently improved only by extending the iteration step. Therefore the introduction of quantum computing mechanism indeed is an effective way to improve the performance of CDE optimization.

5. Conclusion

This paper proposed a quantum inspired differential evolution algorithm. Different from the existing improved method, this method adopted qubit encoding mechanism. For CDE, every dimension variable’s search range of each individual is an internal. While in the proposed algorithm, the variable’s search ranges of every dimension are the Bloch sphere in the three-dimensional space. This algorithm can search the optimized solution on three coordinate axes simultaneously relying on qubit’s pivoting, which can improve the efficiency of optimization. Moreover, the algorithm’s searching range on three coordinate axes is the closed interval. Then the optimized solutions for problem can be gained through the solution space transforms. Therefore, this method does not have to consider about the variable’s value range of every dimension during initialization, which is benefit to make uniform optimization strategy. The experimental results showed that it is available to introduce quantum computing mechanism into CDE algorithm to improve the optimization performance. And it also revealed that the combination of realizing individual coding based on quantum bit, computing rotating angle based on CDE strategy, realizing individual updates based on Bloch sphere can enhance the optimization performance of CDE algorithm.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 61170132).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Price, K., Storn, R. and Lampinen, J. (2004) Differential Evolutionary: A Practical Approach to Global Optimization. Springer, Heidelberg, 183-187.
[2]	Uday, K. (2008) Advance in Differential Evolution. Springer, Heidelberg, 287-293.
[3]	Zhou, Y.Z., Li, X.Y. and Gao, L. (2013) A Differential Evolution Algorithm with Intersect Mutation Operator. Applied Soft Computing, 13, 390-401. http://dx.doi.org/10.1016/j.asoc.2012.08.014
[4]	Zhu, W., Tang, Y., Fang, J.A. and Zhang, W.B. (2013) Adaptive Population Tuning Scheme for Differential Evolution. Information Sciences, 223, 164-191. http://dx.doi.org/10.1016/j.ins.2012.09.019
[5]	Zhang, D.X., Wang, J.H., Gao, L.Q. and Steven, L. (2013) A Modified Differential Evolution Algorithm for Unconstrained Optimization Problems. Neurocomputing, 120, 469-481. http://dx.doi.org/10.1016/j.neucom.2013.04.036
[6]	Musrrat, A., Millie, P. and Ajith, A. (2013) Unconventional Initialization Methods for Differential Evolution. Applied Mathematics and Computation, 219, 4474-4494. http://dx.doi.org/10.1016/j.amc.2012.10.053
[7]	Adam, P.P. (2013) Adaptive Memetic Differential Evolution with Global and Local Neighborhood-Based Mutation Operators. Information Sciences, 241, 164-194. http://dx.doi.org/10.1016/j.ins.2013.03.060
[8]	Cao, A.H., Li, W.C. and Li, L.P. (2009) A Passive Location Algorithm Based on Differential Evolution and Genetic Algorithm Using the Doppler Frequency. Signal Processing, 25, 1644-1648.
[9]	Wang, Y., Cai, Z.X. and Zhang, Q.F. (2012) Enhancing the Search Ability of Differential Evolution through Orthogonal Crossover. Information Sciences, 185, 153-177. http://dx.doi.org/10.1016/j.ins.2011.09.001
[10]	Dilip, D. and Jose, R.F. (2013) A Real-Integer-Discrete-Coded Differential Evolution. Applied Soft Computing, 13, 3384-3393.
[11]	Ali, W.M., Hegazy, Z.S. and Motaz, K. (2012) An Alternative Differential Evolution Algorithm for Global Optimization. Journal of Advanced Research, 3, 149-165. http://dx.doi.org/10.1016/j.jare.2011.06.004
[12]	Ali, W.M. and Hegazy, Z.S. (2012) Constrained Optimization Based on Modified Differential Evolution Algorithm. Information Sciences, 194, 171-208. http://dx.doi.org/10.1016/j.ins.2012.01.008
[13]	Cheng, J.X., Zhang, G.X. and Ferrante, N. (2013) Enhancing Distributed Differential Evolution with Multicultural Migration for Global Numerical Optimization. Information Sciences, 247, 72-93. http://dx.doi.org/10.1016/j.ins.2013.06.011
[14]	Fang, W., Sun, J., Xie, Z.P. and Xu, W.B. (2010) Convergence Analysis of Quantum-Behaved Particle Swarm Optimization Algorithm and Study on Its Control Parameter. Acta Physica Sinica, 59, 3686-3694.
[15]	Li, P.C. and Li, S.Y. (2008) Quantum-Inspired Evolutionary Algorithm for Continuous Spaces Optimization Based on Bloch Coordinates of Qubits. Neurocomputing, 72, 581-591. http://dx.doi.org/10.1016/j.neucom.2007.11.017
[16]	Duan, H.B., Zhang, X.Y. and Xu, C.F. (2011) Bio-Inspired Computing. Science Press, Beijing.