Erratum to “Adaptive Control of DC-DC Converter Using Simulated Annealing Optimization Method” [Journal of Signal and Information Processing, (2014), 5, 198-207] ()
1. Introduction
DC-DC power converters are used in variety of application; including computer systems, office equipment, telecommunication equipment, and other electronics devices. DC-DC converters are electrical circuits that would transfer energy to a load. Electronic switches are used to transfer the energy o energy storage devices and then to load. In DC-DC converters, the switches are either transistors or diodes; whereas capacitors and inductors represent the storage devices. The value of voltage transferred depends on the duty ratios of the switches [1] . The switch is driven by a pulse width modulator PWM. The output signal of the PWM is controlled using a PID controller. The PID gains are tuned using Simulated Annealing optimizers (SA) to improve the transient response of the DC-DC converter.
The simulated annealing optimization method is a statistical optimization technique based on a random search to achieve with high probability a global and an optimum solution [2] . The idea is based on imitating the annealing of a material and then reducing its temperature slowly until a state of thermal stability or equilibrium is reached (minimum energy) [2] .
2. Literature Review
Many researchers have worked in the field of controlling DC-DC conversion. In [3] the authors implemented a dynamic evolution control for boost DC-DC power converter with linear evolution path. In this method, a straight forward analysis of non linear equation models of the converter is used to tune the converter controllers This method is used for digital controller to obtain zero steady state error and wide range of stability.
The authors in [4] presented a genetic algorithm-based PID tuning to optimize the performance of the DC-DC converter. A cascade closed-loop control system was implemented consisting of two loops (outer voltage loop inner current loop). The genetic algorithm was used to optimize the gains of the PID controller for the voltage loop.
In [5] , the paper conducted high current applications; a DC-DC converter of two stages was studied. The converter consists of two three-phase full-bridge inverters. In this study, the converter needs a high power factor at the AC phase and it needs a well regulated voltage at the DC loads. To solve this issue, a control scheme is designed for both inverters, and it is based on a switching function model.
The use of fuzzy control in DC-DC converters is compared with several control methods like hysteresis and sliding mode method. One of the disadvantages of this fuzzy control is there is no procedure for designing the control rule and the membership functions [6] .
The paper in [7] describes a procedure to design a controller for PWM DC-DC converters when there is a large variation in the input reference. The controller has two components: a linear feedback to improve transient response, and a nonlinear feed forward to reject large input disturbances.
3. DC-DC Converter
DC-DC converters at the abstract level are electronic devices used to alter DC voltage from one voltage level to another. The main idea behind the existence of DC-DC converters is that DC voltage cannot be stepped up or stepped down using transformers as in the case of AC voltage [1] .
DC-DC converters use power electronics semiconductor switches operating in “on” and “off” states; and this is because there is a small power loss in those states; i.e. low voltage in the “on” state, and zero current in the “off” state. In order for the DC-DC converter to be smaller in size and lighter in weight; the power electronic switches need to operate in high frequency ranges. High operating frequencies have the advantage of fast dynamic response in the cases where rapid changes in the load current and/or in the input voltage occur [1] .
3.1. Step-Down Buck Converter
A step-down DC-DC converter (buck converter) which is shown in Figure 1 consists of a dc input, a controlled switch, a diode, an inductor, a capacitor, and a load resistor (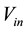 ,
, 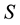 ,
, 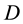 ,
, 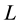 ,
, 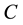 ,
,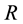 ), respectively.
), respectively.
The switch is a unidirectional voltage switch and implemented with power MOSFETs. The relationship between the input and the output voltages and the switch duty ratio 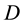 can be illustrated in the following formula with
can be illustrated in the following formula with 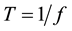 [8] .
[8] .
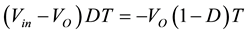 (1)
(1)
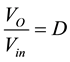 (2)
(2)
![]()
Figure 1. Circuit diagram of a Buck converter.
The buck converter operation can be divided into two periods; one of them when the switch is “on”, and the other when it is “off” [8] .
In the “on” period:
The inductor current can be represented using by:
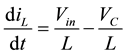 (3)
(3)
and the capacitor voltage can be represented by:
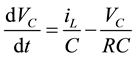 (4)
(4)
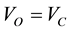 (5)
(5)
In the “off” period:
The inductor current can be represented by:
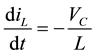 (6)
(6)
and the capacitor voltage can be represented by:
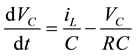 (7)
(7)
![]() (8)
(8)
where, ![]() is the inductor’s current,
is the inductor’s current, ![]() is the voltage across the capacitor,
is the voltage across the capacitor, ![]() is the input voltage and
is the input voltage and ![]() is the output voltage ( both DC voltages).
is the output voltage ( both DC voltages).
The above equations can be rewritten in state space as:
During “on” time:
![]() (9)
(9)
During “off” time:
![]() (10)
(10)
where,
![]() ;;; and
;;; and
Then from equations (9) and (10):
![]() (11)
(11)
where![]() .
.
3.2. Step-Up Boost Converter
A step-up DC-DC converter (boost converter) which is shown in Figure 2 consists of a dc input, a controlled switch, a diode, an inductor, a capacitor, and a load resistor (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ), respectively. The switch is a unidirectional voltage switch and implemented with power MOSFETs.
), respectively. The switch is a unidirectional voltage switch and implemented with power MOSFETs.
The relationship between the input and the output voltages and the switch duty ratio ![]() can be illustrated in the following formula with
can be illustrated in the following formula with ![]() [9] .
[9] .
![]() (12)
(12)
![]() (13)
(13)
The boost converter operation can be divided into two periods; one of them when the switch is “on”, and the other when it is “off” [9] .
In the “on” period:
The inductor current is:
![]() (14)
(14)
and the capacitor voltage is:
![]() (15)
(15)
In the “off” period:
The inductor current is:
![]() (16)
(16)
and the capacitor voltage is:
![]() (17)
(17)
![]() (18)
(18)
where, ![]() is the inductor’s current,
is the inductor’s current, ![]() is the voltage across the capacitor,
is the voltage across the capacitor, ![]() is the input voltage and
is the input voltage and ![]() is the output voltage ( both DC voltages).
is the output voltage ( both DC voltages).
The above equations can be rewritten in state space as:
During “n” time:
![]() (19)
(19)
During “off” time:
![]() (20)
(20)
where,
![]()
Figure 2. Circuit diagram of a Boost converter.
![]() ;;
;;
Then from the Equations (19) and (20)
![]() (21)
(21)
where
![]() (22)
(22)
4. Control Principles
The main goal of DC-DC converters is to provide a regular DC output voltage even in the cases where the load and the input voltage vary. It is known that the values of the converter’s parameters change with time and pressure. Therefore, the controller should be a closed-loop controller with negative feedback. The voltage mode- controller is the most commonly used to control the pulse width modulator PWM [10] , as shown in Figure 3.
In the voltage-mode controller the output voltage is sensed and converted to digital signal using ADC, then it is subtracted from a reference voltage to be fed to a controller; this will generate the control signal of the PWM and the PWM signal will drive the controllable switch (MOSFET) of DC-DC converter. The controller is a PID controller; a Simulating Annealing (SA) optimizer will be used to give an optimum PID controller gains. This will improve the transient response when there is a sudden change in the load of DC-DC converter.
4.1. Simulated Annealing Optimizer
Annealing is the process of heating solid bodies high temperature then allowing it to cool down. The mathematical equivalent of annealing is called simulated annealing and described in [2] [11] .
The process of simulated annealing is represented based on the probability of Boltzmann distribution of energy ![]() at temperature
at temperature ![]() as below [12] :
as below [12] :
![]() (23)
(23)
where
![]() (24)
(24)
![]()
Figure 3. The control system of the DC-DC converter.
4.2. Simulated Annealing Algorithm
In this paper, Simulated Annealing is used to find the certain values among a range of (x, y and z) in order to minimize a certain cost function![]() . The SA algorithm can be summarized as follows [2] [11] :
. The SA algorithm can be summarized as follows [2] [11] :
Step 1: Set initial value of T.
Step 2: Select current set values of![]() ,
, ![]() and
and ![]() from their ranges randomly.
from their ranges randomly.
Step 3: Compute the cost function![]() .
.
Step 4: Select other values of![]() ,
, ![]() and
and ![]() from the same ranges.
from the same ranges.
Step 5: Compute the cost function![]() .
.
Step 6: If the ![]() then:
then:
![]()
![]()
![]()
Step 7: If the ![]() then:
then:
If the ![]() rand then:
rand then:
![]()
![]()
![]()
Step 8: Reduce the temperature T.
Step 9: Repeat Step 3 to Step 8 for n times to obtain the optimum solution.
Figure 4 shows the simulated annealing process described above.
In this work the cost function is:
![]() (25)
(25)
where:
![]()
Figure 4. Simulated annealing process [11] .
![]() (26)
(26)
5. Results and Discussion [13]
A simulated system of Buck and Boost DC-DC converter is built using MATLAB/SIMULINK toolbox. The DC-DC converter is controlled using conventional PID controller and this controller will be tuned using Simulated Annealing optimizer. This is used to improve the transient response of the DC-DC converter.
In this work, the Simulated Annealing algorithm is used to tune the gains of the PID controller, which are used to adjust the output voltage and the reactor current. This reduces the undershoot, overshoot and settling time of the output voltage and reduces the overshoot of the reactor current as will be explained next.
5.1. Step-Down Buck Converter Performance
A simulated transient response of a Buck DC-DC converter is built using Matlab Simulink when the load ![]() changed from 100 Ω down to 5 Ω. In this simulation the circuit parameters are as follow:
changed from 100 Ω down to 5 Ω. In this simulation the circuit parameters are as follow:![]() ,
, ![]() ,
, ![]() ,
, ![]() and the switching frequency
and the switching frequency![]() .
.
Figure 5 shows the transient response for the conventional PID controller. As shown in the figure, the undershoot of the output voltage is 12.5%, the overshoot of the output voltage is 17.3%, the settling time is 14ms and the overshoot of reactor current is 92.3%.
Figure 6 shows the transient response for the Simulated Annealing optimizer. As shown in the figure, the undershoot of the output voltage is 10.4%, the overshoot of the output voltage is 15.4%, the settling time is 13 ms and the overshoot of reactor current is 82.9%.
Table 1 compares the output based on the conventional PID and the SA output for Buck converter. As can be seen from the table, the output voltage undershoot was reduced, the output voltage over was also reduced. The settling time was slightly reduced and the reactor current over shoot was significantly reduced.
![]() (a)
(a)![]() (b)
(b)
Figure 5. Transient response of the conventional PID controller (a) Output voltage; (b) Reactor current.
![]() (a)
(a)![]() (b)
(b)
Figure 6. Transient response of the simulated annealing optimizer (a) Output voltage; (b) Reactor current.
![]()
Table 1. Conventional PID Vs SA output for Buck converter.
5.2. Step-Up Boost Converter Performance
A simulated transient response of a Boost DC-DC converter is built using Matlab Simulink when the load ![]() changed from 100 Ω down to 5 Ω. In this simulation the circuit parameters are as follow:
changed from 100 Ω down to 5 Ω. In this simulation the circuit parameters are as follow:![]() ,
, ![]() ,
, ![]() ,
, ![]() and the switching frequency
and the switching frequency![]() .
.
Figure 7 shows the transient response for the conventional PID controller. As shown in the figure, the undershoot of the output voltage is 21.1%, the overshoot of the output voltage is 9.9%, and the overshoot of reactor current is 46.1%.
Figure 8 shows the transient response for the Simulated Annealing optimizer. As shown in the figure, the undershoot of the output voltage is 19.8%, the overshoot of the output voltage is 9.7%, and the overshoot of reactor current is 45.5%. As can be noticed, the improvement is minimal in this case.
Table 2 summarizes and shows numerical comparison of the results embedded in Figure 7 and Figure 8. And again, seen from the table, the output voltage undershoot was reduced, the output voltage over was also reduced. The settling time was slightly reduced and the reactor current over shoot was slightly reduced as well. These results make the choice of the Boost converter not suitable for this control problem.
![]() (a)
(a)![]() (b)
(b)
Figure 7. Transient response of the conventional PID controller (a) Output voltage; (b) Reactor current.
![]() (a)
(a)![]() (b)
(b)
Figure 8. Transient response of the Simulated Annealing optimizer (a) Output voltage; (b) Reactor current.
![]()
Table 2. Conventional PID vs. SA output for Boost converter.
6. Conclusions
The DC-DC converter is a widely use power electronics circuit. Its output is affected by the variations of some parameters like load, input voltage, temperature, and output voltage. So it is very important to use control system technique to improve the output response. One of the most control technique used is the PID controller. Designing a PID controller is complicated. Therefore, in this work we use the Simulated Annealing Optimizer (SA) to design and tune the PID controller gains.
Simulation results of two types DC-DC converters for sudden changes in the load values are obtained. As shown in the simulation and results chapter, SA achieved an efficient improvement in the output in terms of the output voltage undershot, output voltage overshoot and the reactor current. Though, the buck converter achieved better results.