1. Introduction
In order to explain simple chaotic dynamical systems, one-dimensional map is used. Tent, Bernoulli and Logistic maps are common examples of them. The return map of Tent and Bernoulli are linear, while Logistic map is nonlinear [1] -[3] .
One dimensional map is simple as far as hardware implementation is concerned. In the other hand, security of nonlinear maps is usually more than linear functions. Logistic map is generally used in most of cryptosystems and pseudo random generators. It is used in chaos-based secure communication system and for generations of binary numbers. Li, Mou, and Cai proposed statistical properties of digital piecewise linear chaotic maps and their roles in cryptography and pseudo-random coding [4] . Addabbo proposed performance analysis and optimized design of piecewise linear chaotic maps such as digital saw-tooth and tent maps as a source of pseudo- random bits generators [5] [6] . Pareek used chaotic maps for random bit generator [7] . Shastry, Nagaraj, and Vaidya proposed a generalization of Logistic map, and its applications in generating pseudo-random numbers [8] . Basios, Forti, and Gilbert proposed statistical properties of time-reversible triangular maps of the square [9] . The key element of the cryptosystems is key space. The key space is corresponding to chaotic range. Since chaotic range of logistic map is small, its key space is also small.
In this paper, with the aim of expanding chaotic range of Logistic map, two modified versions of Logistic map are proposed. Definition and properties of Logistic map are reviewed in Section 2. The first and second modified versions of Logistic map are proposed in Section 3. Return maps, orbit diagrams, bifurcation diagrams and Lyapunov exponents were also concerned. Comparison of the modified map with Logistic with respect to their sensitivity to initial conditions, their chaotic range and histograms is considered in Section 4. Finally, conclusion and references are integrated.
2. Logistic Map
Logistic map is one-dimensional map which uses to model simple nonlinear discrete systems. Logistic map explain by a recursive function as follows:
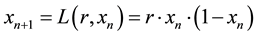 (1)
(1)
where r is its parameter and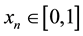 . Consider Logistic map
. Consider Logistic map , given by Equation (1), the parameter r lies in interval
, given by Equation (1), the parameter r lies in interval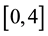 . The return map of Logistic function is given in Figure 1 for
. The return map of Logistic function is given in Figure 1 for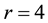 .
.
Sensitivity of Logistic map to initial condition could be observed by plotting orbit diagrams with respect to two initial conditions with small difference. The corresponding orbit diagrams with respect to two initial conditions 0.350 and 0.351 for fixed values of 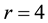 is drawn in Figure 2. There is suitable sensitivity to initial condition.
is drawn in Figure 2. There is suitable sensitivity to initial condition.
In order to view chaotic properties of Logistic map, bifurcation diagram and Lyapunov exponent of it should be calculated and plotted. Bifurcation diagram of Logistic mapwith respect to “r” are calculated and plotted in Figure 3.
Lyapunov exponent of Logistic mapwith respect to “r” are also calculated and plotted in Figure 4. Regarding Figure 3 and Figure 4, Logistic map is chaotic when parameter “r” lies in interval [3.6, 4].
First, confirm that you have the correct template for your paper size.
3. Modified Logistic Maps
A discrete dynamic process is said to be two-segmental if there exists a partitioning point. The general equation
![]()
Figure 1. Return map of logistic map with respect to r = 4.
![]()
Figure 2. Orbit diagrams of logistic map with respect to two initial conditions 0.350 and 0.351 (r = 4).
![]()
Figure 3. Bifurcation diagram of logistic map with respect to r.
![]()
Figure 4. Lyapunov Exponent of Logistic map with respect to r.
of the process could be defined as depicted in Equation (2), such that 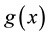 and
and 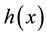 are the left and right hand side functions, respectively [10] [11] .
are the left and right hand side functions, respectively [10] [11] .
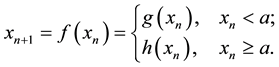 (2)
(2)
where  and
and .
.
The necessary condition for a two segmental function 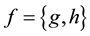 to be a Lebesgue process is that the absolute value of slops must be greater than unity all over the domain [12] . That is, the absolute of derivatives of two branches over the range must be greater than one, Equation (3).
to be a Lebesgue process is that the absolute value of slops must be greater than unity all over the domain [12] . That is, the absolute of derivatives of two branches over the range must be greater than one, Equation (3).
![]() (3)
(3)
As far as Logistic map is concerned, its equation could be separated as follows with respect to![]() :
:
![]() (4)
(4)
Considering Equation (4), the derivatives of ![]() is exceeding unity, but this is not true for
is exceeding unity, but this is not true for![]() . To solve this problem, we use symmetry and transform properties to modify
. To solve this problem, we use symmetry and transform properties to modify![]() . Actually, we modified second part of Logistic map in order to improve chaotic range of Logistic map in two manners.
. Actually, we modified second part of Logistic map in order to improve chaotic range of Logistic map in two manners.
3.1. First Modified Logistic (FML) Map
We modified Logistic map, by obtaining vertical symmetry of ![]() around
around![]() , then transform the result to right for
, then transform the result to right for![]() , to generate a new
, to generate a new![]() . The recursive equation of First Modified Logistic (FML) map is defined in Equation (5), where n is a time index,
. The recursive equation of First Modified Logistic (FML) map is defined in Equation (5), where n is a time index, ![]() is the initial value, and r is the control parameter.
is the initial value, and r is the control parameter.
![]() (5)
(5)
where![]() ,
,![]() . The return map of the result is drawn in Figure 5 for
. The return map of the result is drawn in Figure 5 for![]() .
.
Orbit diagrams of FML map with respect to two initial conditions 0.350 and 0.351 for fixed values of ![]() are drawn in Figure 6. Sensitivity of FML map to initial condition is observed in the graph. There is not suitable sensitivity to initial condition.
are drawn in Figure 6. Sensitivity of FML map to initial condition is observed in the graph. There is not suitable sensitivity to initial condition.
Bifurcation diagram of FML map with respect to “r” are calculated and plotted in Figure 7. Lyapunov exponent of FML map with respect to “r” are calculated and plotted in Figure 9. According to Figure 7 and Figure 8, FML map is chaotic when parameter “r” lies in intervals [2.6, 2.9] or [3.2, 4].
![]()
Figure 5. Return map of FML map with respect to r = 4.
![]()
Figure 6. Orbit diagrams of FML map with respect to initial conditions 0.350 and 0.351 (r = 4).
![]()
Figure 7. Bifurcation diagram of FML map with respect to r.
![]()
Figure 8. Lyapunov exponent of FML map with respect to r.
3.2. Second Modified Logistic (SML) Map
We make another modification to ![]() by symmetries and transformation. Here, we find vertical symmetry of
by symmetries and transformation. Here, we find vertical symmetry of ![]() with axis of symmetry
with axis of symmetry ![]() and horizontal symmetry of the result with axis of symmetry
and horizontal symmetry of the result with axis of symmetry![]() . Then transformation of the result to right with
. Then transformation of the result to right with ![]() is performed. Therefore, recursive equation of Second Modified Logistic (SML) map is forming by modifying
is performed. Therefore, recursive equation of Second Modified Logistic (SML) map is forming by modifying![]() , and is defined in Equation (6):
, and is defined in Equation (6):
![]() (6)
(6)
where n is a time index, ![]() is the initial value,
is the initial value, ![]() and the control parameters
and the control parameters![]() .
.
In order to explain the performance of Equation (6), the return map of the result is drawn in Figure 9.
The orbit diagrams of SML map with respect to two initial conditions 0.350 and 0.351 for fixed value of ![]() are drawn in Figure 10. Sensitivity of SML map to initial condition is observed in the figure. There is superior sensitivity to initial condition.
are drawn in Figure 10. Sensitivity of SML map to initial condition is observed in the figure. There is superior sensitivity to initial condition.
Bifurcation diagram of SML map with respect to ‘r’ are calculated and plotted in Figure 11. Lyapunov exponent of SML map with respect to parameter ‘r’ are calculated and plotted in Figure 12. According to Figure 11 and Figure 12, SML map is chaotic when parameter ‘r’ lies in intervals [2, 4].
![]()
Figure 9. Return map of SML with respect to r = 4.
![]()
Figure 10. Orbit Diagrams of SML map with respect to initial conditions 0.350 and 0.351 (r = 4).
![]()
Figure 11. Bifurcation diagram of SML map with respect to r.
![]()
Figure 12. Lyapunov exponent of SML map with respect to r.
4. Comparison
With the purpose of expanding chaotic range, two modified version of Logistic map are proposed. In order to compare the performance of the proposed maps with respect to applications, orbit diagrams, bifurcation diagram, Lyapunov exponent and histogram of outputs are considered. Orbit diagram shows the sensitivity of the map to initial conditions. Bifurcation diagram and Lyapunov exponent is used to evaluate chaotic behavior of the maps. Histogram of outputs which could be plotted by observing outputs of large number of iterations, simulate probability density function of the maps.
4.1. Sensitivity to Initial Condition (Orbit Diagram)
In order to compare the sensitivity of the proposed maps, FML and SML, with Logistic map to initial condition, their orbit diagrams with respect to two initial conditions with small difference are considered. They are shown in Figure 2, Figure 6 and Figure 10, respectively. As it explained earlier, sensitivity of FML to initial condition is less and sensitivity of SML map to initial condition is more than the others.
4.2. Chaotic Range (Bifurcation Diagram, Lyapunov Exponent)
Bifurcation diagram and Lyapunov exponent of Logistic mapwith respect to “r” are plotted in plotted Figure 3 and Figure 4, respectively. Meanwhile, bifurcation diagram and Lyapunov exponent of FML map are also plot-
ted in Figure 7 and Figure 8. Bifurcation diagram and Lyapunov exponent of SML map are also plotted in Figure 11 and Figure 12. Regarding the related figures, Logistic map is chaotic for![]() , FML map is chaotic for intervals [2.6, 2.9] and [3.2, 4]. In addition, SML map is chaotic for range of
, FML map is chaotic for intervals [2.6, 2.9] and [3.2, 4]. In addition, SML map is chaotic for range of![]() . Therefore, the total chaotic range of SML is more than the others. The comparison of these values is depicted in Table 1. Chaotic range of SML map is fivefold of chaotic range of Logistic map.
. Therefore, the total chaotic range of SML is more than the others. The comparison of these values is depicted in Table 1. Chaotic range of SML map is fivefold of chaotic range of Logistic map.
4.3. Statistical Characteristics (Histogram)
Simulation of probability density function could be performed to show the statistical characteristics of the map. This simulation is run for 10,000 iterations on the map and draws its histogram. Figure 13 shows the histogram result of Logistic map for fixed parameter value of r = 4.
The probability density function of the SML map is also simulated with 10,000 iterations on SML map. Figure 14 shows the histogram of SML map for fixed value of r = 4.
It is appearing that histograms of Logistic map and SML map are identical, while FML map could not perform acceptable result.
5. Conclusions
In order to evaluate the performance of Logistic map, after considering definition and properties of it, orbit diagrams, Lyapunov exponent and histogram of Logistic map were considered. Orbit diagram showed that the sensitivity of Logistic map to initial condition was medium. Bifurcation diagram and Lyapunov exponent were used to evaluate chaotic properties of the map and recognize the range of parameters. The total chaotic range of Logistic map was small.
With the purpose of expanding chaotic range, two modified versions of Logistic map are proposed. They are one-dimensional and two-segmental nonlinear maps. We called them First and Second Modified Logistic (FML & SML). We found vertical symmetry of first segment, transformed the result to right for the second segment, and called it FML map. Definition and properties of FML map were also considered. Sensitivity of FML map to
![]()
Table 1. Comparison of chaotic ranges.
![]()
Figure 13. Histogram of logistic map iterations for r = 4.
![]()
Figure 14. Histogram of SML map iterations for r = 4.
initial condition is not suitable. However, FML map is chaotic when parameter “r” lies in intervals [2.6, 2.9] or [3.2, 4] according to the graphs of bifurcation diagram and Lyapunov exponent. To define a second versionmodified Logistic map, we found vertical and horizontal symmetry of its first segment and transformed the result to right. Recursive equation of Second Modified Logistic (SML) map is forming. Sensitivity of SML map to initial condition is observed in the figure. There is superior sensitivity to initial condition. According to Figure 11 and Figure 12, SML map is chaotic when parameter “r” lies in intervals [2, 4].
It was concluded that sensitivity of FML to initial condition was less and sensitivity of SML map to initial condition was more than the others. Histograms of Logistic map and SML map are identical, while FML map cannot perform acceptable results. The total chaotic range of SML is more than the others. Chaotic range of SML map is fivefold of chaotic range of Logistic map. This property expands key space for cryptographic purposes.