An Estimation of Achievable Rate for Digital Transmissions over MIMO Channels ()
1. Introduction
Achievable rate (AR), defined as information entropy collected from receiving signals―mutual information, is a fundamental means to evaluate and optimize communications. It is demonstrated that AR is inputs related, and achieves its maximum―channel capacity with Gaussian inputs [1] . Despite optimal, Gaussian inputs are rarely used in practice. Instead, digital transmissions with inputs from finite-alphabet constellations, such as m-PSK and etc., are more common, which depart significantly from Gaussian inputs. Therefore, a considerable AR gap exists between the two inputs [2] . Besides, many results have shown that multi-input multi-output (MIMO) greatly improves the performance of digital transmissions [3] . Consequently AR computation for digital transmissions over MIMO channels is motivated.
Reconsider definition of mutual information in [1] . When it comes to finite-alphabet constellations and MIMO propagation matrix, it involves multi-dimensional integral to calculate AR, which leads to impractical implementation. And then various estimations are proposed. Monte Carlo method [4] is the most common. Despite accuracy, not only it is too implicit for analytical applications, but also it costs too much computational complexity as order of modulation and MIMO increases. Particle method [5] is proposed to reduce the complexity. However, it remains implicit. Aiming analytical solution, lower bounds and approximations for AR are proposed in [2] [6] and [7] respectively, showing validity under certain scenarios. Unfortunately, limitation remains. Lower bound in [2] requires unitary inputs―matrix having orthonormal columns [8] . For wireless MIMO channels, such assumption is rarely achieved. As to approximations in [6] [7] , constellations and MIMO channels related tuning factor is indispensable to the estimating accuracy, which also introduces limitation. Moreover, gap between true AR and lower bounds/approximations is not analyzed in the mentioned work.
Comparing to current proposals, the main contribution of this letter is to propose AR estimation of low complexity, analytically explicit expression and controllable gap, without constraints to inputs and MIMO channels. This work is organized as follows. Section 2 formulates the problem and premiss; Section 3 describes details of proposed solution, and analyzes estimating gap; Section 4 gives numerical results, and further discuss on computational complexity and estimating gap; finally conclusions are drawn in Section 5.
2. Problem Formulation
2.1. Notations and Definitions
This work uses the following notations. Italic character in lower and upper case denotes variable. Bold italic character in lower and upper case denotes vector and matrix respectively. The superscript  denotes conjugate transposition.
denotes conjugate transposition. 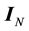 is
is 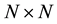 identity matrix.
identity matrix. 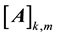 is the element of matrix
is the element of matrix  at
at 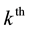 row and
row and 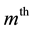 column.
column. 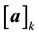 is the
is the  element of vector
element of vector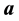 .
. 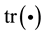 denotes the trace of square matrix.
denotes the trace of square matrix.  is Euclidean norm of matrix and vector.
is Euclidean norm of matrix and vector. 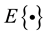 denotes the expectation of random variable.
denotes the expectation of random variable. 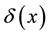 is Dirac delta function.
is Dirac delta function. 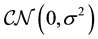 is a complex Gaussian random scalar, and its real and imaginary components are independent and identically normal distributed with zero-mean and variance of
is a complex Gaussian random scalar, and its real and imaginary components are independent and identically normal distributed with zero-mean and variance of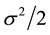 .
. ![]() is a real Gaussian random scalar normal distributed with zero-mean and variance of
is a real Gaussian random scalar normal distributed with zero-mean and variance of![]() .
. ![]() is the complex space, and
is the complex space, and ![]() is the real space.
is the real space. ![]() means that space―
means that space―![]() is consisted of elements―
is consisted of elements―![]() .
. ![]() denotes
denotes ![]() tensor space based on
tensor space based on![]() . Operation
. Operation ![]() is cartesian product of space.
is cartesian product of space.
2.2. Signal Model and Premise
Consider digital transmissions over ![]() MIMO channels, following assumptions are premised.
MIMO channels, following assumptions are premised.
•![]() , is an
, is an ![]() complex propagation matrix, known to receiver.
complex propagation matrix, known to receiver.
•![]() , is an
, is an ![]() transmitted symbol vector.
transmitted symbol vector. ![]() is independently and uniformly selected from
is independently and uniformly selected from ![]() normalized finite-alphabet constellation―
normalized finite-alphabet constellation―![]() :
:![]() . Moreover,
. Moreover, ![]() may differ with
may differ with![]() . Thus
. Thus
![]() (1)
(1)
Define![]() . Consequently
. Consequently![]() :
:![]() , and
, and![]() . So we have
. So we have
![]() (2)
(2)
•![]() , is an
, is an ![]() independent complex additional white Gaussian noise (AWGN) vector, and
independent complex additional white Gaussian noise (AWGN) vector, and
![]() (3)
(3)
•![]() , is an
, is an ![]() receiving symbol vector. Hence, AR is defined as mutual information [1] ,
receiving symbol vector. Hence, AR is defined as mutual information [1] ,
![]() (4)
(4)
Note that, Equation (4) is AR value for the whole transmitting and receiving vector. Considering spatial multiplexing mode of MIMO, AR value for each element in ![]() is also needed, so we formulate the problem as estimation of AR for both vector and each element in the vector.
is also needed, so we formulate the problem as estimation of AR for both vector and each element in the vector.
3. Low-Complexity Solution
Firstly, Equation (4) is rewritten as
![]() (5)
(5)
Given ![]() and
and![]() , the posterior probability is,
, the posterior probability is,
![]()
Given![]() , we have
, we have
![]() (6)
(6)
Definition: Euclidean measure matrix ![]() for given constellation
for given constellation ![]() and
and ![]() is as
is as
![]() (7)
(7)
Recall Equation (3), and then Equation (6) is rewritten as
![]() (8)
(8)
where ![]() is combination of AWGNs,
is combination of AWGNs,
![]() (9)
(9)
Then normalize ![]() as
as
![]() (10)
(10)
So we rewrite Equation (8) as
![]() (11)
(11)
Theorem 1. AR is estimated by exponentially weighted average of Euclidean measure matrix as
![]() (12)
(12)
Proof. see Appendix 1.
Theorem 2. AR is decomposed as
![]() (13)
(13)
where ![]() denotes the sub-vector excluding
denotes the sub-vector excluding ![]() from
from![]() .
.
Proof. see Appendix 2.
With Theorem 1 and 2, the formulated problem in Section 2 is solved.
Theorem 3. Gap between true and estimated AR given in proposition 1 is bounded by exponentially weighted average of minimum Euclidean measure as
![]() (14)
(14)
where ![]() denotes the minimum among non-zero elements in
denotes the minimum among non-zero elements in ![]() column of Euclidean measure matrix.
column of Euclidean measure matrix.
Proof. see Appendix 3.
Recalling Theorem 3, the gap between true and estimated AR for ![]() is
is
![]() (15)
(15)
4. Numerical Results
To verify Theorem 1, 2 and 3, numerical results are provided. For generality, ![]() complex propagation matrixes consisted of independent Gaussian distributed elements are used as MIMO channels,
complex propagation matrixes consisted of independent Gaussian distributed elements are used as MIMO channels,
![]() (16)
(16)
Also high and low correlated scenarios with correlation coefficient of 0.1 and 0.9 are considered respectively,
![]() (17)
(17)
where correlation matrices ![]() and
and ![]() are generated with spatial channel model and correlation coefficient [3] .
are generated with spatial channel model and correlation coefficient [3] .
The 3 transmitted symbols in ![]() are modulated by BPSK, 8PSK and 16QAM respectively. True AR is computed by Monte Carlo method [4] . And estimated AR is computed with Theorem 1 and 2.
are modulated by BPSK, 8PSK and 16QAM respectively. True AR is computed by Monte Carlo method [4] . And estimated AR is computed with Theorem 1 and 2.
Numerical results in Figure 1 and Figure 2 show that the proposed estimation is able to achieve enough accurate AR over complex Gaussian random MIMO channel. And according to Equation (6) and (12), the calculation complexity is reduced to ![]() exponentiations and
exponentiations and ![]() logarithms, instead of
logarithms, instead of ![]() integrals.
integrals.
Despite slightness, numerical results show that the gap remains. However, such estimating gap can be quantized by Equation (14) and (15), and numerical results are shown in Figure 3. According to Figure 1 and
![]()
Figure 1. AR for 2 × 3 random Gaussian distributed MIMO channels with transmitting and receiving correlation coefficient of 0.1.
![]()
Figure 2. AR for 2 × 3 random Gaussian distributed MIMO channels with transmitting and receiving correlation coefficient of 0.9.
![]()
Figure 3. Gap between true and estimated AR for 2 × 3 random Gaussian distributed MIMO channels with transmitting and receiving correlation coefficient of 0.1 and 0.9, computed with Equations (14) and (15).
Figure 2, the maximum gap between estimated and true AR is lower than 0.0733 bits/symbol, which agrees well to theoretic bound of 0.0603 bits/symbol given in Figure 3, which is computed by Theorem 3.
5. Conclusion
A low-complexity AR estimation is presented in this work. Numerical results show that it is accurate enough, and the deductive theoretic bound of estimating gap is well matched. Moreover, the most encouraging thing is that, the proposed estimation is of no constraints to finite-alphabet constellations and MIMO channels. Besides, as shown in Equation (12), this proposition deduces integral of AR calculation into an weighted average of Euclidean measure matrix for given channel states and constellations, which is explicit enough for analytical applications.
Acknowledgements
We thank the Editor and the referee for their comments. This work is funded by the NSFC program (61172021 and 61471030), the Fundamental Research Funds for the Central Universities (2014JBZ023), Beijing city science and technology special program (Z141101004414091), and Research on the development of science and technology plan Chinese Railway Corporation (2014X012-B, Z2014-X002). This support is greatly appreciated.
Appendix
1. Proof of Theorem 1
Proof. Following approximations are easily achieved with numerical methods,
![]() (18)
(18)
Although gap still remains, following deduction will show that such gap makes no difference on AR computations. Define
![]() (19)
(19)
To prove of Equation (12) equals to prove
![]() (20)
(20)
where ![]() is an
is an ![]() ascending sorted vector, and
ascending sorted vector, and
![]() (21)
(21)
Use inductive reasoning, define ![]() as the gap,
as the gap,
![]() . (22)
. (22)
For![]() , recalling Equation (7),
, recalling Equation (7), ![]() constantly equals to 0,
constantly equals to 0,
![]() (23)
(23)
Then assume
![]() . (24)
. (24)
This implies that, within the operative domain of
![]()
following approximation is valid.
![]() (25)
(25)
Recall Equation (18), for![]() , we have
, we have
![]() (26)
(26)
where
![]() (27)
(27)
And the right side of Equation (22) is
![]() (28)
(28)
So that
![]() (29)
(29)
Using monotonic property of exponentiation and logarithm, it is demonstrated that,
![]() (30)
(30)
Recalling Equation (23), (24) and (30), assigning![]() , Equation (21) is proved. And then Theorem 1 is proved by substituting Equation (21) in Equation (11).
, Equation (21) is proved. And then Theorem 1 is proved by substituting Equation (21) in Equation (11).
2. Proof of Theorem 2
Proof. Use ![]() and
and ![]() to denote the sub-set of all possible values of
to denote the sub-set of all possible values of ![]() and
and![]() , and then recall Equation (5), using
, and then recall Equation (5), using ![]() to denote the targeting sub-vector of computation, and
to denote the targeting sub-vector of computation, and ![]() to denote the sub-vector excluding
to denote the sub-vector excluding ![]() from
from![]() . We have,
. We have,
![]() (31)
(31)
Then designate ![]() to denote the sub-vector excluding
to denote the sub-vector excluding ![]() from
from![]() , and Theorem 2 is proved.
, and Theorem 2 is proved.
3. Proof of Theorem 3
Proof. Recall Equation (12) and (30), the maximum gap between true and estimated AR value for ![]() is as follows,
is as follows,
![]() (32)
(32)
Since that the sequence of ![]() is ascending sorted, and then we have,
is ascending sorted, and then we have,
![]() (33)
(33)
Theorem 3 is proved.