A Special Case of Variational Formulation for Two-Point Boundary Value Problem in L2(Ω) ()
1. Introduction
In this paper, we have considered a simple two-point boundary value problem (BVP) for a second order linear ordinary differential equation. Using a maximum principle for this problem, we show uniqueness and continuous dependence on data.
We write the BVP in variational form and use this together (with elements from functional analysis) we prove existence, uniqueness and continuous dependence on data. The finite difference method is a method for early development of numerical analysis to differential equations. In such a method, an approximate solution is sought at the points of a finite grid of points reducing the problem to a finite linear system of algebraic equations [1] .
In this paper, we illustrate this for a two-point BVP in one dimension in which the analysis is based on discrete versions of maximum principle. Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions, see [2] and [3] . We can say that three classes of solution techniques have emerged for solution of BVP for differential equations: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] [7] and [8] .
2. Variational Formulation
We treat the two-point boundary value problem in Hilbert space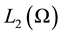 . We consider the problem
. We consider the problem
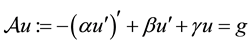
in 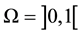 with
with 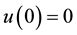 and
and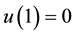 . Here the coefficients
. Here the coefficients 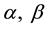 and
and 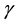 are smooth and
are smooth and
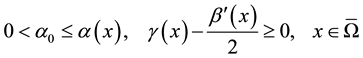
Let 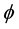 an auxiliary function on
an auxiliary function on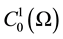 , so multiplying Equation (1) by
, so multiplying Equation (1) by  and integrating over
and integrating over 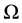 we have
we have
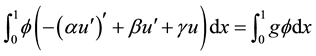
By using integration by parts with 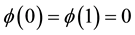 we obtain
we obtain
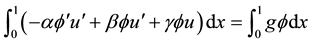
Here (4) is the variational formulation of the problem (1). If we introduce the bilinear form
![]()
with the functional![]() , we can write (3) as
, we can write (3) as
![]()
for all![]() . We can say that function
. We can say that function ![]() is a weak solution of the problem (1) provided that
is a weak solution of the problem (1) provided that ![]() and (6) holds.
and (6) holds.
Next we show two theorems that demonstrate the existence of a solution of the variational equation (6).
Theorem 1. Let ![]() and we assume that (2) holds. Then there exists a unique solution
and we assume that (2) holds. Then there exists a unique solution ![]() of the problem (6) satisfying the condition
of the problem (6) satisfying the condition![]() .
.
Theorem 2. Let ![]() and we assume that (2) holds. Furthermore let
and we assume that (2) holds. Furthermore let ![]() and
and ![]() be the solution of the problem (6), then
be the solution of the problem (6), then ![]() for all
for all ![]() where
where
![]()
In theorem 1, we obtain the weak solution u of (6) and this solution is more regular than stated there, therefore ![]() exists as a weak function (derivative) and
exists as a weak function (derivative) and![]() . Hence, it follows that
. Hence, it follows that ![]() and also
and also
![]()
This expression together with ![]() where
where ![]() implies the regularity estimates
implies the regularity estimates![]() .
.
We can see that the weak solution of (1) is a strong solution, but we can also see that with ![]() less smooth we still obtain a weak solution in
less smooth we still obtain a weak solution in![]() .
.
The next nonlinear boundary problem shows that all solutions are positive by using the strong version of maximum principle.
2.1. Numerical Examples
We consider the nonlinear boundary value problem
![]()
in![]() . In the maximum principle, we need to consider a differential operator
. In the maximum principle, we need to consider a differential operator![]() , i.e. in this case we have
, i.e. in this case we have
![]()
for all![]() . We can see that
. We can see that ![]() usually takes the general form
usually takes the general form
![]()
Therefore, we have ![]() and
and![]() . Now, the maximum principle states that for a differential operator
. Now, the maximum principle states that for a differential operator ![]() and a function
and a function ![]() with the property that
with the property that ![]() in
in![]() , if
, if ![]() in
in![]() , then
, then
![]()
u and ![]() respect the conditions of the principle, the boundary conditions of the problem are
respect the conditions of the principle, the boundary conditions of the problem are![]() . Thus, all solutions of u are
. Thus, all solutions of u are
![]()
The strong version of the principle refers to the case when there is a minimum interior point inside![]() , which results in a constant value of the function u inside the domain
, which results in a constant value of the function u inside the domain![]() . We know already that
. We know already that![]() , and if we assume that u has a minimum point inside
, and if we assume that u has a minimum point inside ![]() say x0 then
say x0 then
![]()
After this assumption, the expression![]() , but
, but ![]() by the initial hypothesis. Here, we have a contradiction, because the assumption that there is a minimum interior point is false. In the other words, the minimum 0 is attained only at the boundaries and all solutions inside the interval
by the initial hypothesis. Here, we have a contradiction, because the assumption that there is a minimum interior point is false. In the other words, the minimum 0 is attained only at the boundaries and all solutions inside the interval ![]() are positive, i.e.
are positive, i.e.
![]()
2.2. Variation Formulation and Existence of ![]()
In this case, we are going to solve
![]()
with the following boundary conditions:
![]()
2.2.1. Solution with BCs: ![]()
Let ![]() an auxiliary function with the homogeneous boundary conditions as u,
an auxiliary function with the homogeneous boundary conditions as u,![]() . Multiplying the initial differential operator
. Multiplying the initial differential operator ![]() and the function f by
and the function f by![]() , then expression (7) becomes
, then expression (7) becomes
![]()
Next, integrate over ![]() we have
we have
![]()
By using integration by parts, we can write the left hand side as
![]()
The last term comes down to 0,
![]()
therefore, the Equation (8) becomes
![]()
which is the variational form of the (7).
Lax-Milgram lemma may allow us to prove existence of a solution. First we consider the LHS and the RHS as a bilinear form and a linear functional respectively, in fact
*![]() (LHS) is a bilinear form because
(LHS) is a bilinear form because ![]() on
on ![]() is a function
is a function![]() . Now it is linear in each argument separately,
. Now it is linear in each argument separately,
![]()
then ![]() is symmetric. To show coercivity of
is symmetric. To show coercivity of![]() , we can apply Cauchy-Schwarz inequality
, we can apply Cauchy-Schwarz inequality
![]()
![]()
Coercivity of ![]() in
in ![]() follows
follows
![]()
*![]() (RHS). We can see that
(RHS). We can see that ![]() is a function
is a function ![]() and L is linear, in fact
and L is linear, in fact
![]()
The Equation (9) can be written as
![]()
since ![]() is a bounded bilinear form, coercive in the Hilbert space
is a bounded bilinear form, coercive in the Hilbert space ![]() and
and ![]() is a bounded linear form in the same space, so the Lax-Milgram theorem states that there exists a unique vector
is a bounded linear form in the same space, so the Lax-Milgram theorem states that there exists a unique vector ![]() i.e. a solution of u exists.
i.e. a solution of u exists.
2.2.2. Solution with BCs: ![]()
Similar to (7), this equation can be written using the auxiliary function ![]() and integration over the domain
and integration over the domain ![]() and
and ![]() in this case.
in this case.
![]()
Therefore, we can see that this function has the same variational formulation, i.e.
![]()
Then, we can use the bilinear form and linear functional. Lax-Milgram lemma shows can be subsequently applied to prove the existence of solution in a similar way as before.
2.2.3. Solution with BCs: ![]()
Let the auxiliary function ![]() with the same boundary conditions
with the same boundary conditions![]() ,
,![]() . In this case, the LHS of (7) can be written as
. In this case, the LHS of (7) can be written as
![]()
We can see that this quantity represents still a bilinear form
![]()
therefore, ![]() on
on ![]() is a function
is a function ![]() and it is linear each argument separately, i.e.
and it is linear each argument separately, i.e.
![]()
![]()
then, ![]() is also symmetric. In this case the coercivity on the Hilbert space
is also symmetric. In this case the coercivity on the Hilbert space ![]() also applies, in fact
also applies, in fact
![]()
hence Lax-Milgram lemma can be applied to
![]()
where ![]() is a bilinear, symmetric coercive form and L a linear functional. A solution of u needs to exist in the domain
is a bilinear, symmetric coercive form and L a linear functional. A solution of u needs to exist in the domain![]() .
.
3. Case of the Beam Equation
In this section, we give the variational formulation for the beam equation and we prove the existence and uniqueness of solution. We consider the beam equation
![]()
with the boundary conditions![]() .
.
Now, using an auxiliary function ![]() with the same BCs as u, and integrating on
with the same BCs as u, and integrating on ![]() we get
we get
![]()
therefore
![]()
Thus, the variational form of the beam equation is
![]()
Again, let the bilinear form and linear functional ![]() and
and ![]() to be equal to
to be equal to
![]()
We can see that ![]() is a function
is a function ![]() and it is linear in each argument separately (as shown previously). Finally
and it is linear in each argument separately (as shown previously). Finally ![]() is also symmetric, i.e.
is also symmetric, i.e.
![]()
Here, the Lax-Milgram theorem can be applied to this system and show existence of a solution for u.
Note: In mechanical representations, the boundary conditions ![]() represent the
represent the
![]()
Figure 1. Solutions using the finite difference method (11) for (a) h = 1/10 and (b) h = 1/10. (c) Error when comparing these 2 grid choices with the exact solution. (d) Logarithmic plot of the error vs. the choice of h.
deflection and the slope of the deflection at the boundaries is 0 which means that the ends of the beam are fixed.
4. Maximum of the Error at the Mesh-Points for 2-Point BVP
In this example, we consider the two-point boundary value problem [9]
![]()
with![]() . Applying the finite difference method
. Applying the finite difference method
![]()
with ![]() we show in Figure 1 the exact solution and the maximum of the error at the mesh-points.
we show in Figure 1 the exact solution and the maximum of the error at the mesh-points.
Figure 1(a) and Figure 1(b) present similar plots. However, a h twice as small decreases the maximal error a 4 fold, shown in Figure 1(c). At the same point x = 0.6, the error is 2.209 × 10−5 vs. 8.829 × 10−5. The Logarithmic plot in Figure 1(d) shows a linear relationship between the error and h with slope 8 units.
Acknowledgements
We would like to thank the referee for his valuable suggestions that improved the presentation of this paper and group GEDNOL of the Universidad Tecnológica de Pereira-Colombia.