On the Derivation and Implementation of a Four Stage Harmonic Explicit Runge-Kutta Method* ()
1. Introduction
During the last few decades, there has been a growing interest in problem solving systems based on the Runge- Kutta methods. Several methods have been developed using the idea different means such as the geometric mean, centroidal mean, harmonic mean, contra-harmonic mean and the heronian mean.
In previous papers [1] and [2] , the authors presented a three stage method based on the harmonic mean and a multi-derivative method using the usual arithmetic mean respectively. Akanbi [3] developed a third-order method based on the geometric mean. In [4] and [5] , the concept of the heronian mean was introduced. Evans and Yaacob [6] introduced a fourth-order method based on the harmonic mean while Yaacob and Sanugi [7] also developed a fourth-order method which is an embedded method based on the arithmetic and harmonic mean. Wazwaz [8] presented a comparison of modified Runge-Kutta methods based on varieties of means. Using the definition of the harmonic mean, a fourth-order Runge-Kutta method is developed and implemented.
2. Derivation of the 4sHERK Method
The schemes introduced by [7] and [9] respectively are
 (1)
(1)
where




and
 (2)
(2)
where
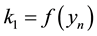


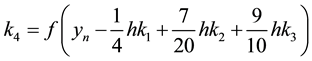
Scheme (2) was referred to as RK-HM-AM. Using the definition of harmonic mean, the following scheme is proposed in this paper:
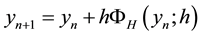 (3)
(3)
where,
 (4)
(4)

 (5)
(5)
 (6)
(6)
 (7)
(7)
where ![]() and
and ![]() are constants to be determined.
are constants to be determined.
The expansion of ![]() and
and ![]() as defined above give
as defined above give
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Substituting (8), (9) and (10) into (4) and simplifying the resulting expression using MATHEMATICA (version 8.0.1) package, the coefficients of the powers of h in (4) are compared with that of the Taylors’ expansion of ![]() and upon solving the resulting system of non-linear equations we have
and upon solving the resulting system of non-linear equations we have
![]() ; (11)
; (11)
Thus, the incremental function (4) of the proposed scheme is
![]() (12)
(12)
and the proposed scheme (3) is
![]() (13)
(13)
where
![]()
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
3. Stability of the 4sHERK Method
For the analysis of the absolute stability of the proposed 4sHERK scheme, the scalar test problem ![]() with solution
with solution ![]() is used, where
is used, where ![]() is a complex variable (see [10] ). With the above test problem, we have
is a complex variable (see [10] ). With the above test problem, we have
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Substituting (17)-(20) in (3) and simplifying the resulting expression results in,
![]() (21)
(21)
Letting ![]() and evaluating
and evaluating ![]() from (21), the stability polynomial of the proposed scheme is obtained as
from (21), the stability polynomial of the proposed scheme is obtained as
![]() (22)
(22)
The absolute stability region of the 4sHERK scheme is given in Figure 1.
4. Error Estimation
Definition: The local truncation error at ![]() of the explicit one step method (3) is defined to be
of the explicit one step method (3) is defined to be ![]() where
where
![]()
And ![]() is the theoretical solution (See [10] ).
is the theoretical solution (See [10] ).
Using the above definition together with (12), the local truncation error (LTE) of the proposed scheme is given as
![]() (23)
(23)
![]()
Figure 1. Absolute stability region of the 4sHERK method.
where ![]() is obtained by Taylor series expansion.
is obtained by Taylor series expansion.
5. Numerical Experiments
Consider the IVP
![]() (24)
(24)
with the theoretical solution
![]() (25)
(25)
We apply the new 4sHERK method (13) to the above IVP and the results obtained are compared with the classical 4-stage fourth-order Runge-Kutta method and the methods of [6] and [4] .
The results generated by the newly derived scheme in this paper evidently proved the extent of accuracy of the scheme in comparison with the other methods.
6. Conclusion
Evidently, the newly derived scheme is more accurate as seen from the computational results presented in Table 1, Table 2 and Table 3, since its absolute error is the least of all the methods presented in this paper. It therefore follows that the scheme is quite efficient. We therefore conclude that the 4sHERK method proposed is reliable, stable and with high accuracy in computation.
NOTES
*Four Stage Harmonic Runge-Kutta Method.