Sound Quality Prediction of Vehicle Interior Noise under Multiple Working Conditions Using Back-Propagation Neural Network Model ()
1. Introduction
With the development of automobile industry, vehicle noise problem has been paid increasing attention all over the world. Correspondingly, sound quality has become an important index to measure the quality of automotive products. Recently, many studies related to sound quality evaluation (SQE) of vehicle noise have been investigated by researchers, and many achievements were acquired. Shu [1] studied the relation between psychological assessment indexes and subjective annoyance at the same speed of different cars, and demonstrated that the linear combination of psychoacoustic parameters is feasible to evaluate the stationary vehicle sound quality. Chen [2] investigated sound quality preference of vehicle interior noise under stationary condition and built a preference prediction model using multi-dimensional linear regression method. Shen [3] predicted the sound quality of vehicle interior noise at constant speed with three methods: MLR, back-propagation neural network and support vector machine; the results showed that support vector machine is most accurate in vehicle SQE. Xu [4] researched sound samples collected at the position of the driver’s ear and obtained the conclusion that the annoyance model can correctly predict subjective preference of the sound samples. Wang [5] predicted sound quality of vehicle interior noise under non-stationary conditions effectively based on a wavelet pre-processing neural network model. But the in-situ studies scarcely involve in the issue that the vehicle noises under multiple working conditions are included in one model.
Vehicle interior noise signal under stationary working condition of a vehicle is easy to be measured and evaluated. The non-stationary interior noise, which keeps changing with the vehicle speed, is very complicated. How to evaluate the non-stationary sound so that the evaluated results can reflect perception of candidates accurately is a difficult problem for SQE engineers. It is important for modern vehicle to develop new methods, which can efficiently estimate the sound quality under multiple working conditions. Thus, based on the back- propagation neural network (BPNN), a SQP model for multi-working conditions’ vehicle interior noise is built in this paper. By this model, human auditory perception for vehicle interior noise can be described quantitatively with the model outputs, subjective annoyance values.
2. BP Network Theory
The BPNN [6] is a common method for training artificial neural networks in conjunction with an optimization method, such as the gradient descent. The method calculates the gradient of a loss function with respects to all the weights in the network. The gradient is fed to the optimization method which in turn uses it to update the weights, in an attempt to minimize the loss function. Back propagation (BP) requires a known, desired output for each input value in order to calculate the loss function gradient. It is therefore usually considered to be a supervised learning method, although it is also used in some unsupervised networks. It is a generalization of the delta rule to multi-layered feed forward networks, made possible by using the chain rule to iteratively compute gradients for each layer. The BP requires that the activation function used by the artificial neurons (or “nodes”) be differentiable. Figure 1 shows a typical structure of a 3-layer BP neural network.
Given the number of nodes of the input layer, the hidden and the output network n, k, m, respectively, the total number of input samples is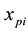 , which indicates that the P sample’s the ith input value,
, which indicates that the P sample’s the ith input value, 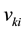 indicates the ith node of input layer to the hidden layer of the kth node weight,
indicates the ith node of input layer to the hidden layer of the kth node weight, 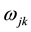 means the node weight from hidden layer of
means the node weight from hidden layer of
![]()
Figure 1. A typical 3-layer BP neural network structure.
the k to the output layer of the j. For convenience, the threshold is included connection weights, and then the output of hidden layer node k is:
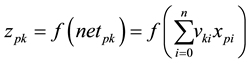 (1)
(1)
The output layer nodes for the node j:
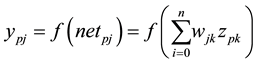 (2)
(2)
where, standard sigmoid function is selected as incentive function:
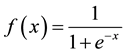 (3)
(3)
The definition of global error functions can be expressed as:
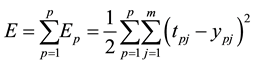 (4)
(4)
where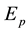 , is error of the sample
, is error of the sample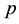 ,
, 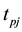 is the ideal output. The adjustment formulas of weights are as follows.
is the ideal output. The adjustment formulas of weights are as follows.
a) The weight adjustment formula of output layer neurons:
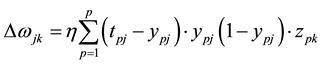 (5)
(5)
where, 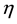 is the learning rate, whose general range is 0.1 - 0.3.
is the learning rate, whose general range is 0.1 - 0.3.
b) The weight adjustment formula of each hidden layer neurons:
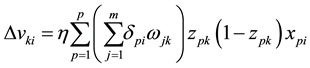 (6)
(6)
The basic idea of the BP algorithm is the learning process and can be divided into two stages: the first stage (forward propagation process), given input information through a layer by layer processing each hidden layer and calculate the actual output value of each unit of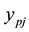 ; the second stage (the reverse process), if the output layer fails to get the expected output value, then layer by layer recursively calculates the difference of error between the actual output and the expected output. The gradient descent method modifies the weights of the
; the second stage (the reverse process), if the output layer fails to get the expected output value, then layer by layer recursively calculates the difference of error between the actual output and the expected output. The gradient descent method modifies the weights of the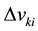 ,
, ![]() , making the total error function minimum.
, making the total error function minimum.
3. BPNN-SQP Model for Multiple Working Conditions’ Vehicle Interior Noise
3.1. Road Tests and SQE for Samples
The vehicle noise signals under the conditions of idle, constant speed, accelerating and braking are acquired by road tests in this paper. The test conditions are carefully constructed referring to the measurement method for vehicle interior noise using GB/T 18697 standard [7] , which has similar settings for the test environment and conditions as the standards ISO 5128 [8] and ISO 362 [9] . With the LMS multichannel data acquisition system, the interior noises of three kinds of B-class car are measured. The noise signals at each position are recorded 3 times under each working condition. The best samples of each car are picked out. Totally 36 noise signal samples are acquired and subjectively evaluated. Sound annoyance is defined as 11 grades (shown in Table 1) and the jury tests are performed with 26 volunteers (18 men and 8 women), who are composed of engineers, experts, technicians and drivers. With the LMS software, six psychoacoustic parameters, such as the loudness, sharpness, roughness, articulation index, tonality and A-weighted sound pressure levels (SPLs) of the measured 36 samples are calculated. The subjective and objective evaluated results are listed in Table 2, which will be used for BPNN-SQP modeling in the following text.
![]()
Table 1. Ranks of subjective annoyance.
![]()
Table 2. Results of the subjective and objective evaluation of vehicle interior noise.
3.2. Correlation Analysis and Significance Test
For checking the correlations between calculated psychoacoustic indices and the subjective annoyance values, the SPSS software is adopted for Pearson correlation analysis. The correlation coefficients and two-tailed test results are listed in Table 3, where SQ is the subjectively evaluated annoyance, AW is the A-weighted SPL; L is the loudness; S is the sharpness; AI is the articulation index; R is the roughness; T is the tonality.
According to the Pearson correlation analysis in Table 3, the correlation coefficients of the roughness and tonality are too low, which means the roughness and tonality indices can be excluded in sound annoyance evaluation. The A-weighted SPL, loudness, AI index and sharpness, which have higher correlation with the sound annoyance, is selected as the input values for establishing the BPNN-SQP model in this paper.
3.3. Model Construction
The BPNN-SQP model is constructed with MATLAB software in this paper. The measured 36 interior noise samples are used for model establishment. After relative analyzing and normalization processing, these data are divided into two groups, in which samples no. 1 - 24 are selected as training data, The rest samples no. 25 - 36 are used as testing data in order to verify the accuracy of the BPNN-SQP model. With correlation analysis and significance test, the final evaluation model is built within permissible error.
3.3.1. Input and Output Layer Nodes
Sound annoyance has higher correlations with A-weighted sound pressure, loudness, AI index, and sharpness, as shown in Table 3. Therefore, this paper selects these parameters to establish the BPNN-SQP model as the input value.
3.3.2. Normalization of Sample Data
To build a uniform SQP model, signal amplitudes of the samples directly influence accuracy of the BPNN-SQP model. Before inputting the sample data to the model, sample normalizations should be conducted. In this paper, the sample data are compressed in a range of [0, 1], according to Equation (7).
![]() (7)
(7)
3.3.3. Determination of Network Parameters
The S-type of hidden layer and the linear output layer in a 3-layer BPNN can approximate any function [10] . In the present work, the 3-layer BP neural network as shown in Figure 1 is determined to build a sound quality prediction model. Considering the hidden layer selection rules, after testing, the hidden layer number is set to 7. The logsig, purlin linear functions are selected as transfer functions of the hidden layer and the output layer, respectively. The samples no. 1 - 24 is fed to the neural network for training. The training parameters of network are very important, which direct impact on the network performance. In this paper, the expected error is set to 0.003, the learning rate is 0.3, and the momentum factor is 0.5. After repeated tests, and the final echo number in training is 5000 times.
3.3.4. Prediction Results and Analysis
Taking the optimal parameters obtained from the training data, the BPNN-SQP model with multi-working conditions is used to predict sound quality (annoyance) of vehicle interior noise. To check the model accuracy, firstly, the A-weighted SPLs, loudness, sharpness, AI index of the training samples are fed to as the model and the predicted annoyance values are compared with those from jury tests in Figure 2. Further analysis shows that, the prediction accuracy of the model is above 95.57%, which satisfy the requirement of error percentage within 10%. Moreover, annoyances of the test samples no. 25 - 36 are estimated by using the BPNN-SQP model, the estimated results are compared with the subjective annoyance values in Figure 3. We obtained an averaged estimation error of 9.11%, which suggests a good accuracy of the newly established BPNN-SQP model in SQE of vehicle interior noises.
4. Conclusion
Taking the vehicle interior noises under multiple working conditions, this paper established a BPNN-SQP model, using some objective evaluation parameters, such as A-weighted sound level, loudness, AI index and sharpness
![]()
Table 3. Correlations of subjective annoyance (SA) values and psychoacoustic parameters.
**Correlation is significant at the 0.01 level (2-tailed); *Correlation is significant at the 0.05 level (2-tailed).
![]()
Figure 2. Comparison of estimated values and original values with the training samples.
![]()
Figure 3. Comparison of estimated and tested values with the measured noise samples.
et al., as input, and subjective annoyance values as output. By applying this model to predict unknown noise samples, the averaged relative error of predicted results comparing with the actual results is 9.11%. The BPNN- SQP model for multi-condition of vehicle interior noise has high accuracy of prediction forecasting and good generalization ability.
Acknowledgements
This work has been supported by the NSFC (Grant no. 51175320), and partly supported by the Program for Special Appointment Professor (Eastern Scholar) at the Shanghai Institutions of Higher Learning, China.
NOTES
*Corresponding author.