1. Introduction
The homotopy analysis method is developed in 1992 by Liao [1]-[8]. It is an analytical approach to get the series solution of linear and nonline arpartial differential equations. The difference with the other perturbation methods is that this method is independent of small/large physical parameters. It also provides a simple way to ensure the convergence of series solution [9]. This method has been successfully applied to solve many linear and non linear partial differential equationsin various fields of science and engineering by many authors [1]-[16]. The homotopy analysis method is useful and efficient for obtaining both analytical and numerical approximations of linear or nonlinear differential equations. In this study, we will concentrate on exact solutions for equations type of 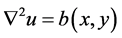 and
and 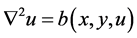 frequently used in applied and engineering mathematics.
frequently used in applied and engineering mathematics.
2. The Engineering Equations on an Elliptical Domain
We refer to the problem given by Partridge and Brebbia [17]. Consider the following engineering equations
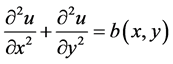 (1)
(1)
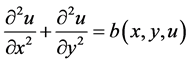 (2)
(2)
where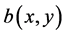 , that is, considered to be a known function of position and
, that is, considered to be a known function of position and 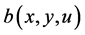 will be considered as a known function of the potential.
will be considered as a known function of the potential.
In all applications, the domain bounded by the ellipse given in Figure 1 will be used. The boundary condition is the Dirichlet condition with 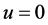 on the boundary.
on the boundary.
The equation of the ellipse is
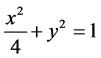 (3)
(3)
3. Homotopy Analysis Method
We apply the HAM to equations of the type  and
and 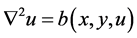 with Dirichlet boundary con- dition. We consider the following differential equation
with Dirichlet boundary con- dition. We consider the following differential equation
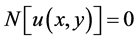 (4)
(4)
where 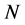 is a linear operator,
is a linear operator, 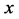 and
and ![]() are independent variables,
are independent variables, ![]() is an unknown function. In HAM, the zeroth-orderde formation equation is constructed as
is an unknown function. In HAM, the zeroth-orderde formation equation is constructed as
![]() (5)
(5)
where
![]() (6)
(6)
![]() is an auxiliary parameter,
is an auxiliary parameter, ![]() is an initial guess,
is an initial guess, ![]() is an auxiliary parameter and
is an auxiliary parameter and ![]() is the embedding parameter. Applying the homotopy-derivative [4]
is the embedding parameter. Applying the homotopy-derivative [4]
![]() (7)
(7)
To both sides of Equation (5), we get the following mth-order deformation equation
![]() (8)
(8)
where
![]() (9)
(9)
And
![]()
Figure 1. Elliptical domain with Dirichlet boundary condition.
![]() (10)
(10)
Note that ![]() for
for ![]() can be obtained by solving the linear Equation (8) with linear boundary conditions that come from original problem. If the power series Equation (6) of
can be obtained by solving the linear Equation (8) with linear boundary conditions that come from original problem. If the power series Equation (6) of ![]() converges at
converges at![]() , then we gets the following series solution:
, then we gets the following series solution:
![]() (11)
(11)
4. Applications
We apply Homotopy Analysis Method to equations of the type ![]() and
and![]() , as follows:
, as follows:
Equation (1) suggests that we define an equation of linear operator as
![]() (12)
(12)
And Equation (2) suggests that we define an equation of linear operator as
![]() (13)
(13)
Using the above definitions, the zeroth-orderde formation equation is constructed as
![]()
Applying the homotopy-derivative to the zeroth-orderde formation equation, we obtain the following mth- orderde formation equations
![]()
Since![]() ,
, ![]() , now the solution of the mth-orderde formation equation becomes
, now the solution of the mth-orderde formation equation becomes
![]() (14)
(14)
where
![]() (15)
(15)
![]() (16)
(16)
Example 1. Consider the equation of the type ![]()
![]() (17)
(17)
With initial guess
![]() (18)
(18)
using HAM, were cursively obtain
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]()
![]() (25)
(25)
When![]() , we obtain the exact solution as follows:
, we obtain the exact solution as follows:
![]() (26)
(26)
![]() (27)
(27)
Example 2. Consider the equation of the type ![]()
![]() (28)
(28)
with initial guess
![]() (29)
(29)
using HAM, were cursively obtain
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]()
![]() (36)
(36)
When![]() , we obtain the exact solution as follows:
, we obtain the exact solution as follows:
![]() (37)
(37)
![]() (38)
(38)
Example 3. Consider the equation of the type ![]()
![]() (39)
(39)
with initial guess
![]() (40)
(40)
using HAM, were cursively obtain
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]()
![]() (47)
(47)
For![]() , we obtained the closed form series solution as
, we obtained the closed form series solution as
![]() (48)
(48)
![]() (49)
(49)
which is the exact solution.
Example 4. Consider the equation of the type ![]()
![]() (50)
(50)
with initial guess
![]() (51)
(51)
using HAM, were cursively obtain
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
![]()
![]() (58)
(58)
For![]() , we obtained the closed form series solution as
, we obtained the closed form series solution as
![]() (59)
(59)
![]() (60)
(60)
which is the exact solution.
Example 5. Consider the equation of the type ![]()
![]() (61)
(61)
with initial guess
![]() (62)
(62)
using HAM, were cursively obtain
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
![]() (67)
(67)
![]() (68)
(68)
![]()
![]() (69)
(69)
For![]() , we obtained the closed form series solution as
, we obtained the closed form series solution as
![]() (70)
(70)
![]() (71)
(71)
which is the exact solution.
5. Conclusion
In this paper, the homotopy analysis method has been applied to solve some of engineering problems defined on an elliptical domain. Exact solutions for equations of the type ![]() and
and ![]() are obtained using the HAM. Obviously for
are obtained using the HAM. Obviously for ![]() the obtained solutions are as the same Reference [17]. There sults show that HAM is very efficient technique in finding the exact solutions for equations of the type
the obtained solutions are as the same Reference [17]. There sults show that HAM is very efficient technique in finding the exact solutions for equations of the type ![]() and
and ![]() having wide applications in engineering mathematics.
having wide applications in engineering mathematics.