Solution of Delay Differential Equations Using a Modified Power Series Method ()
1. Introduction
Although both ordinary differential equations (ODEs) and delay differential equations (DDEs) are used to describe physical phenomena, they are different. While in ODEs the derivatives of unknown functions are dependent on only the current value of the independent variable, in addition to this in DDEs, the derivatives of unknown functions are dependent on the values of the functions at previous time. This implies that the solution of DDEs requires the knowledge of the current state and the state at certain previous times.
Some of the application areas of delay differential equations are population dynamics, infectious disease, physiological and pharmaceutical kinetics, chemical kinetics, models of conveyor belts, urban traffic, heat exchangers, robotics, navigational control of ships and aircrafts, and more general control problems (see [1] -[4] ).
There are a few classes of nonlinear ODEs for which solutions can be easily found and despite the obvious similarities between ODEs and DDEs, solutions of DDE problems can differ from solutions for ODE problems in several striking and significant way [5] . Delay problems always lead to an infinite spectrum of frequencies. Therefore, they are solved by numerical methods, asymptotic solution, approximations and graphical approaches [6] . As a result of a dramatic increase in the application of delay models, many authors have investigated and proposed various methods for solving DDEs, Spline methods (see [7] -[9] ), Homotopy Analysis Method (HAM) [10] , Homotopy perturbation method (HPM) [11] , Adomain decomposition method (see [12] -[14] ), Iterative decomposition method [15] and Variation Iteration Method (VIM) [6] .
In this paper, we consider a modified power series method for solving the delay differential equations of the form.
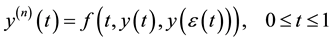(1)
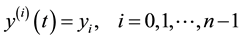(2)
where n and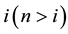 
denote the order of derivatives.
2. Description of the Method
According to the MPSM, the Nth degree approximate solution to the DDE (1)-(2) is given by
(3)
where
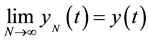(4)
The MPSM is described by the following five-step procedure:
Step 1
Rewrite Equation (1) such that only the nonhomogeneous term is on the right hand side of the equation
Step 2
On the left hand side of the nonhomogeneous differential equation, substitute
(5)
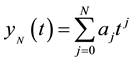(6)
and the derivatives of 
up to order n. However, if the nonhomogeneous term or a coefficient of y or its derivative is not a polynomial but analytic at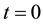
, then replace it by its Taylor series expansion of degree N about
.
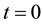Step 3
Collect the power of t on the left hand side of the equation resulting from step 2 and set the coefficient of each power of t on the left hand side equal to the corresponding coefficient on the right hand side of the equation.
Step 4
Solve, using either the Newton’s method or forward substitution method, the first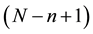 
equations resulting from Step 3 (these are the equations obtained by equating the coefficients of the corresponding powers of t from 
up to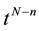
) together with the n equations generated by the associated given conditions to find
,
.
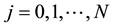Step 5
Substitute the coefficients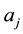 
determined in Step 4 into Equation (3) to obtain an approximate solution of degree N to the delay differential Equation (1)-(2).
3. Illustrative Examples
Example 3.1 (see [8] [9] [15] )
Consider the first-order nonlinear DDE
![]()
(7)
Subject to
![]()
(8)
Applying the proposed method illustrated in section 2 to this problem for the cases N = 3, 5, 7, 8, 11, we obtain as follows:
![]()
Obviously,
![]()
which is the exact solution to Example 3.1.
Example 3.2 (see [7] [8] [10] [15] )
Consider the second-order linear DDE
![]()
(9)
Subject to
![]()
(10)
Using the proposed method for![]()
, we obtain ![]()
which is the exact solution to this example.
Example 3.3 (see [8] [9] [12] [15] )
Consider the third-order nonlinear DDE
![]()
(11)
Subject to the conditions
![]()
(12)
with the proposed method illustrated in section 2, we obtain for the cases N = 5, 7, 9, 11 and 13 as follows:
![]()
Clearly,
![]()
which is the exact solution to Example 3.3.
Example 3.4 (see [6] [10] [12] )
Consider the first-order linear DDE
![]()
(13)
Subject to
![]()
(14)
The exact solution is given by ![]()
For![]()
, the present method yields in turn
![]()
which converges to ![]()
the exact solution to Example 3.4.
4. Conclusion
A simple and straight forward technique based on the power series method has been studied for the solution of delay differential equations. This new approach is implemented without using restrictive assumptions or adding perturbation term and it gives excellent performance compared with existing techniques for solving delay differential equations.