Adaptation of the Two Sources of Code and One-Hot Encoding Method for Designing a Model of Microprogram Control Unit with Output Identification

Łukasz Smoliński^*, Alexander Barkalov, Larysa Titarenko

Institute of Computer Engineering and Electronics, University of Zielona Góra, Zielona Góra, Poland.

DOI: 10.4236/ica.2015.62012                

Abstract

This article presents a proposal for a model of a microprogram control unit (CMCU) with output identification adapted for implementation in complex programmable logic devices (CPLD) equipped with integrated memory modules [1]. An approach which applies two sources of code and one-hot encoding has been used in a base CMCU model with output identification [2] [3]. The article depicts a complete example of processing for the proposed CMCU model. Furthermore, it also discusses the advantages and disadvantages of the approach in question and presents the results of the experiments conducted on a real CPLD system.

Keywords

CPLD, PAL, UFM, CLB, Two Sources of Code, One-Hot Encoding, CMCU

1. Introduction

Nowadays, complex programmable electronic systems are applied for implementing logic circuits of control units [4] - [9] . However, the issue of reducing the size of a control unit is still a subject of current interest [10] [11] . Reducing the size of used resources makes it possible to improve such indicators as: the speed of performance, power consumption and the size of the realised unit [12] [13] . One of the methods for reducing the size of the control unit is the realization of the control algorithm with the use of the CMCU (compositional microprogram control unit) project methodology [14] . The application of CMCU makes it possible to implement a much smaller number of logical functions realising the task of the control system. The existing project methods based on the CMCU are not dedicated to the solutions realized with the use of programmable devices (CPLD). CPLDs include macrocells of programmable array logic (PAL) with a limited number of terms. To reduce the amount of hardware in the logic circuit of a control unit, the peculiarities of the CPLD and the features of a control algorithm to be implemented should be taken into account. Some of the CPLD family devices are equipped with integrated memory. For example, Altera CPLD devices are equipped with user flesh memory (UFM) [15] , whereas Cypress CPLD devices are equipped with cluster memory blocks (CMB) [16] . This article presents a mathematical model and a design algorithm with two sources of code and one hot encoding which has been adopted to CMCU model with output identification [1] .

2. Background of the CMCU with Output Identification

It is assumed that the graph-scheme of the algorithm (GSA) is represented by sets of vertices where

and a set of arcs E where. It is further assumed that and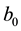

is an initial vertex, is a final vertex, is a set of operator vertices, is a set of conditional vertices. A

vertex contains a microinstruction and is a set of data-path microoperations [17] . Each vertex contains a single element of a set of logical conditions

. A set C of operational linear chains (OLC) for the GSA shall be formed, where each OLC is a sequence of operator vertices and each pair of its adjacent components corresponds to an arc of the GSA.

(1)

Each OLC has only one output and an arbitrary number of inputs. The elements are understood as a state of the system which is identified by elements. OLC outputs make up the collection. Each vertex from corresponds to microinstruction stored in the control memory (CM) of CMCU and it has an address. The microinstructions can be addressed using R bits, where

(2)

and the bits are represented by variables from the set T:

(3)

The project methodology of the microprogram control unit with output identification offers specific positioning of microinstructions in the memory, so as to make it possible to determine the state of the unit, using possibly the smallest number of address signals. The algorithm of positioning microinstruction in the memory consists of the following steps:

1. First, all microinstruction addresses are coded with the use of natural encoding.

2. The value of is set to.

3. An address table is created. The table consists of columns defined as of older address bits, and lines defined as younger address bits, where, following Equation (2).

4. If the outputs i of two different OLC chains, where belong to the same column and neither of the outputs is connected with the end vertex of the network of operations, then the data are moved to the right, beginning with the first vertex of the chain. The released cells are determined as “insignificant” with the symbol. The operation of moving to the right is repeated until the outputs and are placed in separate columns of the table.

5. If all the output vertices are uniformly represented by, then the algorithm moves to step 7.

6. If the address of any vertices reaches beyond the range of the current addressing, then:. Next, the algorithm returns to step 4.

7. The end.

The codes for each microinstruction are formed as a concatenation of the table’s columns and lines. In such a case, the outputs of the OLC chain are uniformly encoded using variables from the set where:

(4)

The algorithm for designing a model of the CMCU with output identification consists of the following steps:

1. Formation of the set of OLCs.

2. Addressing microinstructions (with shifting operation) and encoding OLC elements.

3. Formation of the control memory content.

4. Formation of the transition table of the CMCU.

5. Formation of the excitation function for the counter.

6. Synthesis of the logic circuit of CMCU.

Figure 1 shows a logical scheme of the CMCU with output identification. The pulse causes loading of the first microinstruction address into a counter CT and set up of a fetch flip-flop TF. If, then microinstructions can be read out of the control memory CM. If a current microinstruction does not correspond to an OLC output, then a special variable is formed together with microoperations. If, then content of the CT is incremented according to the addressing mode. Otherwise, the block of CC generates functions. If equals 1, then the CMCU stops and new data from the CM will be not loaded.

3. Main Idea behind the Proposed Method

It shall be pointed out that the logic for the CC and CT is implemented as parts of the CPLD. An external PROM chip or memory integrated with the CPLD may be applied to implement the CM. The memory has t outputs, where [18] . Some information can be implemented using free outputs of the CM. It is assumed that one-hot encoding of microoperations is used. The word of the CM has

(5)

The outputs of the CM are free:

(6)

The bits are represented by variables from the collection P:

(7)

If conditions

(8)

take place, the method can be used. As for encoding additional information used by excitation functions for the CT, one-hot encoding will be applied. In such a case, the amount of information that can be stored in free CM is:

(9)

Next, an occurrence table is created, with columns and. The column contains the OLC elements, whereas the column shows the number of occurrences of an OLC element while making an excitation function for the CT. The number of occurrences of the element is counted on the basis of a transition table, where a number of high bits is counted in addresses corresponding to. Using the occurrence table, it is now possible to transfer the of the most frequently used elements to a new collection:

(10)

It shall be noted that the collection has been divided into two collections and, where

Figure 1. Structural diagram of the CMCU with output identification U₁.

(11)

For the CMCU model with output identification and two sources of code, the memory CM is a source of variables used for encoding the elements through codes. The of the oldest output bits from the counter CT is a source of variables from the set used for encoding the elements through codes.

It shall be highlighted that the maximum length of the logical expressions used for making excitation functions which use the information from the source for the base method of the CMCU with output identification is:

(12)

For the proposed model with one hot encoding, the maximum length of the logical expressions built on the basis of the information from the collection does not change and equals:

(13)

The maximum length of logical expressions for the model with one hot encoding, built on the basis of the information from the collection, is reduced and equals:

(14)

As a result, the value of the CM and the transition table have been modified on the basis of the occurrence table.

The modified algorithm for designing a model of the CMCU with output identification consists of the following steps:

1. Formation of the set of OLCs.

2. Addressing microinstructions (with shifting operation) and encoding OLC elements.

3. Formation of the control memory content.

4. Formation of the transition table of the CMCU.

5. Formation of the occurrence table.

6. Modification of the control memory content.

7. Modification of the transition table of the CMCU.

8. Formation of the excitation function for the counter and minimization.

9. Synthesis of the logic circuit of CMCU.

Figure 2 presents a modified structure of the CMCU with output identification and the applied method of two sources of code.

4. An Example of the Proposed Method

Figure 3 and Figure 4 present an exemplary algorithm used for the realization by the control unit. This algorithm employs the following variables:, , , , , , , , , , , , , ,. First, an initialization Table 1 of microinstruction addresses is formed.

Figure 2. Modified structural diagram of the CMCU with output identification U₂.

Figure 3. An example of the algorithm used for the realisation of T₁.

Table 1. Initial table of addressing.

Figure 4. Operation chains for the algorithm T₁.

Next, the shift operation takes place, resulting in a new address Table 2. Thanks to the shift operation, all the elements may be identified using of older address bits:. With the use of Table 2, Table 3 is created, containing encoding for operation chains, as well as Table 4, with the content of the CM. Finally, a transition Table 5 is created.

Let us assume that we have a memory module in which. Following the above-presented modification,

the calculations may be put forward as:, , , where is the number of free CM bits which will be represented by a set of variables. On the basis of Table 5,

an occurrence Table 6 is created. For the purpose of this example, high values in address bits (there are 7 of them) corresponding to the element have been bolded and underlined in Table 5. The collection is di-

vided into collections and. As a result: and. Next, elements from the collection are encoded with the use of variables from the set P. As a result:,

. Column 3 in Table 5 contains modified encoding for the OLC elements with a second source of information about the state of the unit, which is a CM module. Table 4 is modified with additional data informing about the state of the unit. These data have been marked with an underlining and bolding in columns and. The last step is the construction of an excitation function based on the modified data from columns 3 and 4 of Table 5:

Table 2. Table of addressing after shift operation.

Table 3. OLC elements encoding.

Table 4. Microinstruction encoding.

Table 5. Transition table.

Table 6. Occurrence table.

5. Results and Conclusions

Figure 5 presents the results of the implementation of the model in real hardware. The Alter, a family MAX II device EPM1270 F256C5 equipped with UFM, has been used for tests. Figure 5 depicts the relationship between the obtained reduction in the size of the system (in percentage) and the participation of the source of data in generating the excitation functions (in percentage). The results of conducted experiments indicate that the ability to reduce the length of the terms make it possible to reduce the size of the system. In the analyzed model, in some cases, the deterioration of the possibility of minimizing the functions has a greater impact than reducing the length of the terms, which results in an increase in the size required for the realization of the designed system. With such scenarios, an algorithm consisting of the following steps might serve as an alternative:

Figure 5. Reduction in the size of the system due to the participation of the source.

1. Formation of the set of OLCs.

2. Addressing microinstructions (with shifting operation) and encoding OLC elements.

3. Formation of the control memory content.

4. Formation of the transition table of the CMCU.

5. Construction of excitation functions for the CT and RG.

6. Minimization of excitation functions.

7. Finding logical expressions―OLC elements which have not undergone minimization―in the minimized excitation functions.

8. Formation of the occurrence table containing most frequently occurring OLC elements which have not undergone minimization.

9. Modification of the control memory content.

10. Modification of the transition table and CM of the CMCU.

11. Formation of the excitation function for the counter and minimization.

12. Synthesis of the logic circuit of CMCU.

Taking the OLC elements, which do not undergo minimization to the collection will make it possible to avoid the effect of degradation of minimization possibilities in excitation functions. This effect appears in the scenarios with minor participation of the source in the construction of the excitation functions. The solution presented in this paper requires formalization of mathematical descriptions and adaptation to specific CMCU models. This proposal also requires conducting implementation experiments based on real reprogrammable devices. Future studies will focus on designing mathematical models based on the above-presented algorithm and comparing the results obtained with the results for the models using the method of two sources of code [2] [3] [19] -[21] .

Information

Mr. Łukasz Smoli?ski is a scholar within Sub-measure 8.2.2 Regional Innovation Strategies, Measure 8.2 Transfer of knowledge, Priority VIII Regional human resources for the economy Human Capital Operational Programme co-financed by European Social Fund and state budget.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Wisniewski, R. (2009) Synthesis of Compositional Microprogram Control Units for Programmable Devices. University of Zielona Gora Press, Poland.
[2]	Barkalov, A., Titarenko, L. and Smoliński, L. (2014) CMCU Model with Base Structure Dedicated for CPLD Systems. Przeglqd Elektroniczny, 12, 25-29.
[3]	Barkalov, A., Titarenko, L. and Smoliński, L. (2012) Optimization of Control Unit Based on Construction of CPLD, Pomiary, Automatyka, Kontrola, 58, 93-96.
[4]	Monmasson, E., Idkhajine, L., Cirstea, M., Bahri, I., Tisan, A. and Naouar, M. (2011) FPGAs in Industrial Control Applications. IEEE Transactions on Industrial Informatics, 7, 224-242. http://dx.doi.org/10.1109/TII.2011.2123908
[5]	Kania, D. (2004) The Logic Synthesis for the PAL-Based Complex Programmable Logic Devices. Zeszyty Naukowe, Elektronika, 14, 5-212.
[6]	Kubica D. and Kania D. (2011) Synteza logiczna zespolu funkcji ukierunkowana na minimalizacje liczby wykorzystywanych bloków logicznych PAL w oparciu o zmodyfikowany graf wyjsc. Pomiary, Automatyka, Kontrola, 57, 737-740.
[7]	Monmasson, E. and Cirstea, M. (2007) FPGA Design Methodology for Industrial Control Systems—A Review. IEEE Transactions on Industrial Informatics, 54, 1824-1842. http://dx.doi.org/10.1109/TIE.2007.898281
[8]	Garcia-Vargas, I., Senhadji-Navarro, R., Jimenez-Moreno, G., Civit-Balcells, A. and Guerra-Gutierrez, P. (2007) ROM-Based Finite State Machine Implementation in Low Cost FPGAs. IEEE International Symposium on Industrial Electronics, Vigo, 4-7 June 2007, 2342-2347. http://dx.doi.org/10.1109/ISIE.2007.4374972
[9]	Rafla, N. and Davis, B. (2006) A Study of Finite State Machine Coding Styles for Implementation in FPGA. 49th IEEE International Midwest Symposium on Circuits and Systems, Puerto Rico, 6-9 August 2006, 337-341.
[10]	Czerwiński, R. and Kania, D. (2009) Synthesis of Finite State Machines for CPLDs. International Journal of Applied Mathematics and Computer Science, 19, 647-659. http://dx.doi.org/10.2478/v10006-009-0052-0
[11]	Anand, B.P. and Saravanan, C.G. (2012) Development of Research Engine Control Unit Using FPGA-Based Embedded Control System. Journal of KONES Powertrain and Transport, 19, 9-18.
[12]	Salauyou, V. and Grzes, T. (2007) FSM State Assignment Methods for Low-Power Design. 6th International Conference on Computer Information Systems and Industrial Management Applications, 2007, CISIM ’07, Minneapolis, 28-30 June 2007, 345-350.
[13]	Czerwinski, R. and Kania, D. (2012) Area and Speed Oriented Synthesis of FSMs for PAL-Based CPLDs. Microprocessors and Microsystems, 36, 45-61. http://dx.doi.org/10.1016/j.micpro.2011.06.004
[14]	Barkalov, A. and Titarenko, L. (2008) Logic Synthesis for Compositional Microprogram Control Units. Springer, Berlin.
[15]	Altera (2007) Using the UFM in MAX II Devices. www.altera.com/literature/an/an489.pdf
[16]	Cypress (2003) Delta39K ISR CPLD Family. http://pdf.datasheetcatalog.com/datasheet2/9/0pfaeyx4ushkk0zzjksaycgxhqky.pdf
[17]	Baranov, S. (2008) Logic and System Design of Digital Systems. TUT Press, Tallin.
[18]	Maxfield, C. (2004) The Design Warrior’s Guide to FPGAs: Devices, Tools and Flows. Elsevier, Amsterdam.
[19]	Barkalov, A., Titarenko, L. and Smoliński, L. (2013) Hardware Reduction for Compositional Microprogram Control Unit Dedicated for CPLD Systems. Proceedings of IEEE East-West Design and Test Symposium-EWDTS 2013, Rostov-on-Don, 27-30 September 2013, 1-6. http://dx.doi.org/10.1109/EWDTS.2013.6673200
[20]	Barkalov, A., Titarenko, L. and Smoliński, L. (2014) The Application and Adaptation of the Two Sources of Code and Natural Encoding Method for Designing a Model of Microprogram Control unit with Base Structure. Circuits and Systems, 5, 301-308. http://dx.doi.org/10.4236/cs.2014.512031
[21]	Barkalov, A., Titarenko, L. and Smoliński, L. (2011) Optimization of Microprogram Control Unit with Code Sharing. Proceedings of IEEE East-West Design & Test Symposium-EWDTS 2011, Sevastopol, 9-12 September 2011, 55-59. http://dx.doi.org/10.1109/EWDTS.2011.6116573