1. Introduction
The description of recession can have a variety of applications in hydrologic studies, including the evaluation of aquifer properties and the sustainability of ground-water discharge. Low flow characteristics have been increasingly utilized in recent years as the demand for water has increased. Information on low flow characteristics provides threshold values for different water-based activities and is required for water resource management issues such as water supply, irrigation, and water quality and quantity estimates. An understanding of the outflow process from groundwater or other delayed sources is also essential in studies of water budgets and catchment response.
The most commonly used method of modelling baseflow recession is to use a linear store. This method has a long history, and was first noted in the literature by Boussinesq in 1877 [1] . It was further developed and applied in the first half of the 20th century by Maillet [2] and was popularised in 1939 by Barnes [3] . The flow from a receding aquifer Q is linearly related to storage S.
Although the linear model of recession can be a reasonable approximation, there are a number of processes that will affect recession-curve shape, some causing departures from linearity [4] -[6] .
Aksoy, Bayazit and Wittenberg [7] used a probabilistic approach in order to model nonlinear storage processes. In 2004, Aksoy used Markov chains to simulate no perennial daily streamflow data [8] . In this paper, a probabilistic approach is proposed to model the recession flow of springs from a Bayesian point of view.
2. Theoretical Aspect
Figure 1 evidences that, for a constant time interval Δt, the flow interval ΔQ decreases with time t. Then, it can be stated that:
(1)
Increasing with Δt but decreasing with t, according to Bayes’s theorem:
(2)
the following probabilistic equations can be deduced:
![]()
Figure 1. Typical curve of recession flow.
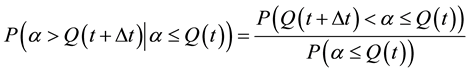(3)
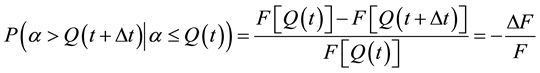(4)
F is the cumulative distribution function (CDF) of the recession flow Q(t).
2.1. Case1
Let’s consider that the conditional probability is only proportional to the time interval Δt. This condition is not sufficient because the flow interval, which increases with the time interval, also decreases with time.
(5)
If Δt tends toward dt, the solution of Equation (5) is Boussinesq’s equation [1] and Maillet’s equation [2] :
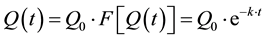(6)
Q0 is the initial flow at t = 0.
2.2. Case 2
Let’s consider that the conditional probability is proportional to the time interval and inversely proportional to time. This case reflects the behaviour of the recession flow
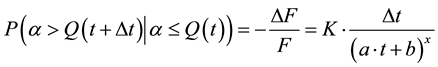(7)
with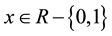
. If Δt tends toward dt, the solution of Equation (7) is:
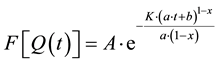(8)
At t = 0,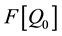 
is equal to 1, therefore:
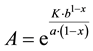
And
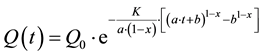(9)
If x = 0 and b = 0, Equation (9) gives Maillet’s formula [2] . If b = 0, Equation (9) gives Horton’s formula [4] .
2.3. Case 3
Let’s consider that x = 1 in Equation (7):
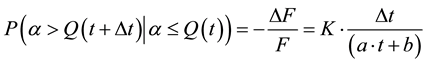(10)
If Δt tends toward dt, the solution of Equation (10) is:
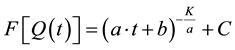(11)
As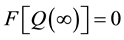
, then C = 0. As![]()
, then b = 1. Therefore, the equation of the recession flow is:
![]()
(12)
Equation (12) is similar to the equation derived by Wittenberg [5] :
![]()
(13)
With
![]()
Equation (13) is related to a power-law reservoir which is suitable for springs, unconfined aquifer and soil moisture.
Equation (12) is similar to Boussinesq’s equation [1] :
![]()
(14)
With k/a = 2. Equation (14) is suitable for shallow unconfined aquifer.
Equation (12) is similar to the equation of Griffiths and Clausen [9] :
![]()
(15)
With k/a = 3. Equation (15) is suitable for surface depression storage such as lakes and wetlands.
Equation (12) is similar to:
![]()
(16)
With k/a =1 and![]()
. Equation (17) is related to exponential reservoir and is suitable for modelling throughflow in soil.
Equation (12) is similar to Coutagne’s equation [10] :
![]()
(17)
With ![]()
and![]()
.
Equation (12) is similar to the following equation related to underground caverns reservoir [9] :
![]()
(18)
With k/a = ‒1, ![]()
and ![]()
2.4. Groundwater Memory Effect
Do these equations reflect a Markovian process or not? In other words, does the future flow depend on the former or not? The answer can be found by the following equation:
![]()
(19)
By combining Equations (6) and (19), it can be found that for Maillet’s equation:
![]()
(20)
![]()
does not depend on![]()
; the process is Markovian.
For Equation (9):
![]()
(21)
![]()
depends on t, therefore on![]()
; the process is not Markovian.
For Equation (12):
![]()
(22)
The process is also not Markovian.
The non-Markovian character of Equations (9) and (13) means that the groundwater storage exhibits a memory effect.
3. Tests and Discussion
3.1. Results
Twelve spring recession flow series (Table 1) are analysed in order to validate the probabilistic approach proposed in this paper. Nine springs are located in USA. The data are provided by the U.S Geological Survey (http://waterdata.usgs.gov/nwis.). Two springs are located in France [11] and one spring is located in ex Montenegro [12] . Rewriting Equation (9) with b = 0 gives:
![]()
(23)
With ![]()
and ![]()
The computed results of Equations (12) and (23) have been compared with the measured data of the springs. The results are recapitulated in Table 1 and an example of comparison between experimental and computed data
![]()
Table 1. Location of springs. Fitting parameters of equations.
is illustrated by Figure 2.
3.2. Volume of Water Released
For each spring, the volume of water released during the recession duration can be computed by:
![]()
(24)
Equation (24) is a discrete sum. T is the duration of the recession. The volume released can also be computed in a continuous point of view by:
![]()
(25)
![]()
(26)
![]()
is the Euler gamma function and ![]()
is the incomplete gamma function.
The Euler gamma function satisfies:
![]()
The incomplete gamma function satisfies:
![]()
Equation (26) has a limiting value when the duration t is important (mathematically, when the duration t approaches infinity):
![]()
Figure 2. Recession flow versus time. Bennet spring-Missouri.
![]()
(27)
Equation (25) also has a limiting value when the duration is important and when λ > 1:
![]()
(28)
On the other hand, if λ < 1, Equation (25) does not have a limiting value when the duration t is important:
![]()
(29)
That means if Equation (25) with λ < 1 is used for computing the released volume by the spring and if the recession duration is important, the error made on the calculation of this volume can be large. In this case, Equation (26) is more suitable than Equation (25) although it is a little less powerful to simulate the recession flow.
In a general way, Equation (12) is a little more powerful than the Equation (23) to simulate the recession flows. However, for the calculation of released volume, in the case of a long period of recession, the Equation (26) will have to be used because if the parameter λ of the Equation (12) is less than one, the integral of Equation (12) (Equation (25)), mathematically speaking, does not have limiting value if λ < 1.
3.3. Storage-Outflow Model
It was shown in 1.3 that Equation (13) was similar to the Equation (14) derived by Wittenberg [5] with![]()
.
He suggested a value of b = 0.5 for average conditions even if the true value of b is not exactly met. The assumption of b = 0.5 would be more physically based and better fitting for the majority of river basins than the linear reservoir.
Equation (14) is related to the following power-law reservoir:
![]()
(30)
It is obvious that if λ < 1, Equation (13) can not be related to the power-law reservoir described by Equation (30) because b should be negative.
Table 1 gives the value of λ which is more than one only for Crnojevica spring and Mill spring. For all the other springs, λ is between zero and one. In this case, what is the conceptual model that explains Equation (12)?
The volume released is computed by Equation (25) which can be rewritten as:
![]()
(31)
If S0 is the initial volume of groundwater in the aquifer, then, at time t, the groundwater storage is:
![]()
(32)
A general storage-outflow relation can be expressed by:
![]()
(33)
With ![]()
![]()
![]()
The conceptual model expressed by Equation (33) explains the recession flows of the springs for which the exponent l of Equation (13) is less than one.
4. Conclusions
A simple analysis of a classical recession curve leads to conclude that this natural phenomenon is generally not a Markovian process. That means that a future value of the recession flow depends on the former and that ground- water reservoir exhibits a memory effect. The Bayesian approach makes it possible to give a probabilistic mean- ing to recession flow equations derived according to a physical approach.
The probabilistic approach can lead to derive general equations of recession flow which can be transposed to complex reservoir for which the physical approach could be difficult to use.
The logical continuation of this work would be used to determine the contributions which the probabilistic approach could have for river recession flow which is more complicate to model than spring recession flow because the recession curves are related to overland flow then to subsurface flow and, finally, to groundwater flow. For advances in recession analysis, the probabilistic approach can be an alternative when the physical processes governing recession flow are unclear.