Enhancing Groundwater Quality through Computational Modeling and Simulation to Optimize Transport and Interaction Parameters in Porous Media ()
1. Introduction
According to a 2013 report of the World Health Organization ([1] and references therein), there are over 780 million people without access to clean drinking water. Over 50% of the United States population receives its drinking water from groundwater, water that flows underneath the earth’s surface in aquifers [2] . Largely due to the recent surge in industrial processes, contaminants have been introduced into groundwater, reducing the amount that can be used for drinking and requiring more expensive treatment processes. Recent incidents of water contamination [3] include radionucleotides leaking from reactors in Fukushima, Japan; petroleum spilling from crude oil pipeline in Yellowstone River, Montana; and a benzene spill in Songhua, China. Studies in the past decade also have shown that colloids, collections of nanoparticles, can destroy these contaminants through chemical reactions. One example is zero-valent iron nanoparticles, which use oxidation-reduction reactions to neutralize toxic metal ions [4] . It is thus important to understand the movements of colloidal particles in the system defined by the groundwater and porous medium that it flows through. In the past couple decades, a few models have been introduced to describe this system. An extensive presentation of the evolution of the current state of surface water and ocean water contamination models can be found in Bahadur et al. One can also find suitable mathematical models for groundwater flow in [5] and parameter identification models in [6] . A large number of suite of codes have been developed by U.S. Salinity Laboratory (USSL) and the University of Cali- fornia, Riverside (UCR) in the last three decades. Simunek et al. describe the historical development and applications of the HYDRUS and STANMOD software packages and related codes.
The STANMOD suite builds off analytic models developed from 1980, including CFITM and CXTFIT, which accounts for particle degradation and the equilibrium state at a single reaction site. The numerical HYDRUS model released in 1991 includes temperature dependent kinetic coefficients and allows for two reac- tion sites [7] . One of the models MNM1D [8] , which is introduced in the last few years, introduces non-linear reaction sites and kinetic coefficients dependent upon salt concentrations. It is based on the following major components of the system: the diffusion of the nanoparticles in the fluid and the transport of them between the liquid and solid phases through reaction sites. Other features of the model include variable hydrochemical parameters that depend on the diffusion of salts and reaction sites of both the linear and Langmuirian type. This model was tested by Tosco and Sethi against both the STANMOD and HYDRUS-1D models, and the MNM1D closely matched these.
Although the existing model encompasses the previous mentioned properties, there are still additional im- provements that can be made. In this study, the flow velocity of the fluid was assumed to be non-constant, governed by the Darcy-Forchheimer fluid model. The electromagnetic interactions that occur in the fluid were also introduced by adding an electric field term based on the Helmholtz-Smoluchowski equation to the men- tioned fluid model. In addition, a parameter estimation algorithm was implemented for a single kinetic coefficient. These parameters govern the ionic strength of the surrounding groundwater, potentially giving researchers the ability to attribute certain characteristics to the liquid.
The structure of the paper is as follows. Section 2 introduces the mathematical model and governing dif- ferential equations. Section 3 describes the implementation of the governing system via implicit finite-difference discretization. In Section 4, we present computational experiments for a benchmark application that involves step-wise injection of nanoparticles. This application, which was presented in [9] , was successfully validated. The application was enhanced and implemented with the inclusion of the non-constant flow model and electro- magnetic effects. Experimental data was simulated to quantify one of the kinetic transport coefficients in order to identify the ionic strength of the groundwater. The computational framework along with the results provided in this paper suggests that the enhanced model presented is a reliable candidate for evaluating potential real- world solutions to contaminated aquifers.
2. Mathematical Models and Background
Transport of colloids is governed by advection-dispersion phenomena and particle-soil interactions. Colloidal particle transport in porous systems is modeled using a modified advection-dispersion equation. It describes the dual-phase, non-equilibrium interactions between particles in the liquid and solid phase. Colloid deposition on the grain surface is generally referred to as attachment, colloid release from the surface as detachment. Earlier theories, such as the classical filtration theory (CFT) consider first-order attachment kinetics, but consider the detachment ones to be negligible. However, MNM1D includes both phenomena in the particle-soil interactions. The physical system described is summarized in Figure 1 below.
Several 1D forms of the model have been proposed, each taking into account some or all of the above characteristics. However, we can write the general form of the modified advection-dispersion equation for the colloid movement taking into account the liquid-solid phase transfer:
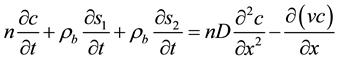 (1)
(1)
where:
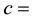 The colloid number concentration in the liquid phase.
The colloid number concentration in the liquid phase.
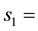 The number colloid concentration in the solid phase at the first reaction site.
The number colloid concentration in the solid phase at the first reaction site.
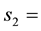 The number colloid concentration in the solid phase at the second reaction site.
The number colloid concentration in the solid phase at the second reaction site.
 The bulk density of the solid matrix.
The bulk density of the solid matrix.
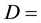 The hydrodynamic dispersion coefficient.
The hydrodynamic dispersion coefficient.
 The Darcyan flow velocity.
The Darcyan flow velocity.
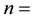 The porosity of the packed bed.
The porosity of the packed bed.
Many types of reaction sites exist, and thus there are many models that describe the mass transfer between the solid and liquid phases. MNM1D takes into account two reaction sites. The first is assumed to have blocking phenomena, and so the colloid concentration at the site is limited to a fixed values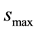 . The transfer can be described by:
. The transfer can be described by:
 (2)
(2)
where:
 The attachment coefficient at site 1.
The attachment coefficient at site 1.
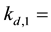 The detachment coefficient at site 1.
The detachment coefficient at site 1.
 The maximum particle concentration for site 1.
The maximum particle concentration for site 1.
The second site is assumed to have a linear exchange term, and so the transfer can be described as:
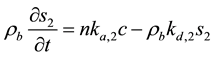 (3)
(3)
where:
 The attachment coefficient at site 2.
The attachment coefficient at site 2.
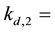 The detachment coefficient at site 2.
The detachment coefficient at site 2.
The hydrochemical parameters, such as ionic strength, can be correlated with the concentration of some conservative tracer, such as salt. The transport of the tracer can also be described by the advection-dispersion equation as:
![]() (4)
(4)
where:
![]() The conservative salt concentration.
The conservative salt concentration.
The concentration of the tracer ultimately affects the values of the attachment/detachment kinetic coefficients. The functional relationship between the salt concentration and kinetic coefficients below was proposed in [8] .
![]()
![]()
![]()
where:
![]() Asymptotic value of
Asymptotic value of![]() .
.
![]() Critical deposition concentration.
Critical deposition concentration.
![]() Critical release concentration.
Critical release concentration.
![]() Asymptotic value of
Asymptotic value of![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() Empirical coefficients determined by breakthrough curves of kinetic coefficients.
Empirical coefficients determined by breakthrough curves of kinetic coefficients.
Finally, we now introduce a fluid model to describe the flow velocity of the groundwater over time and space. Here, we will implement the Darcy-Forchheimer model [10] , which has specific applications to groundwater flow. The model is governed by the following differential equations:
![]() (5)
(5)
![]() (6)
(6)
where:
![]() Pressure of the fluid.
Pressure of the fluid.
![]() Viscosity of the fluid.
Viscosity of the fluid.
![]() Permeability of the fluid.
Permeability of the fluid.
![]() Inertial factor of the fluid.
Inertial factor of the fluid.
![]() Density of the fluid.
Density of the fluid.
We now wish to introduce how the presence of electromagnetics affects this model. To do this, we will turn to a modified version of the above fluid model goverened by the Helmholtz-Smoluchowski (H-S) equation as discussed in [11] . The H-S equation relates the electric field present in the groundwater with physical characte- ristics of the system:
![]() (7)
(7)
where:
![]() Electric field.
Electric field.
![]() Dielectric permittivity of fluid.
Dielectric permittivity of fluid.
![]() Zeta potential.
Zeta potential.
![]() Fluid conductivity.
Fluid conductivity.
As described by Fourie, the fluid model then becomes:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where:
![]() Electrokinetic coupling coefficient.
Electrokinetic coupling coefficient.
3. Implicit Finite Difference Solution Methodology
In this section, we will develop an implicit finite difference scheme to solve the coupled system Equations (5)- (14). To rewrite the derivatives of![]() ,
, ![]() ,
, ![]() , and
, and![]() , we first consider the following finite difference approximations for some function
, we first consider the following finite difference approximations for some function ![]() expressed as:
expressed as:
![]()
![]()
![]()
where![]() . In order to solve this system, we first need values of
. In order to solve this system, we first need values of![]() ,
, ![]() , and
, and![]() . We can extract these values from Equations (8)-(10). Using a central difference approximation, we can write Equation (8) as:
. We can extract these values from Equations (8)-(10). Using a central difference approximation, we can write Equation (8) as:
![]()
which implies
![]()
We now see that in order to solve for pressure, we require initial values for ![]() at
at ![]() for all interested positions, and that this equation is independent of the rest of the system. We now rewrite Equation (9) as:
for all interested positions, and that this equation is independent of the rest of the system. We now rewrite Equation (9) as:
![]()
We can solve for ![]() using the quadratic formula, and so we have
using the quadratic formula, and so we have
![]()
We see here that ![]() also appears to be independent of our interested quantities. However, to make the model more realistic, one could assume that
also appears to be independent of our interested quantities. However, to make the model more realistic, one could assume that ![]() is a function of the local concentration of the nanoparticles,
is a function of the local concentration of the nanoparticles,![]() .
.
Note, for the sake of simplicity, we will assume![]() ,
, ![]() , and
, and ![]() to be constant. The values will be determined by those used in Tosco and Sethi. Using the approximations, Equations (1)-(4) can be rewritten as:
to be constant. The values will be determined by those used in Tosco and Sethi. Using the approximations, Equations (1)-(4) can be rewritten as:
![]()
![]()
![]()
![]()
We can now solve for our interested quantities, ![]() and
and ![]() from the previous equations to yield
from the previous equations to yield
![]() (11)
(11)
![]() (12)
(12)
and by a similar method, we can solve for ![]() and
and ![]() to get
to get
![]() (13)
(13)
![]() (14)
(14)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . We
. We
can write Equations (11)-(14) in matrix form as
![]() (15)
(15)
where
![]()
![]()
![]()
![]()
![]()
With![]() ,
, ![]() ,
, ![]() , and
, and![]() . Letting
. Letting![]() , Equation (15) can be rewritten as
, Equation (15) can be rewritten as
![]() (16)
(16)
Due to the non-linearity that exists in matrix![]() , Equation (16) is a non-linear system. We will use Newton’s Method to approximate the solution to this non-linear system. If
, Equation (16) is a non-linear system. We will use Newton’s Method to approximate the solution to this non-linear system. If ![]() is the
is the ![]() iteration of the solution vector
iteration of the solution vector![]() , then
, then
![]() (17)
(17)
where the Jacobian ![]() and
and ![]() are defined as:
are defined as:
![]()
![]()
![]()
Equation (17) can be rewritten as:
![]() (18)
(18)
The solution is now obtained iteratively by calculating the residuals ![]() and updating the solution so that
and updating the solution so that ![]() at each node within the computational domain. This process is repeated until the difference between the successive solution is within a prescribed tolerance. The numerical method was validated to be quadratically convergent.
at each node within the computational domain. This process is repeated until the difference between the successive solution is within a prescribed tolerance. The numerical method was validated to be quadratically convergent.
4. Computational Experiments
In this section, we perform the following computational experiment which will be used to validate the results from [9] to the one presented in this study. We will consider a line segment from ![]() m to
m to ![]() m, with a step-wise injection of nanoparticles at
m, with a step-wise injection of nanoparticles at ![]() m for the first 200 s. The values of the relevant constants, which were retrieved from [12] -[16] , used are listed in Table 1 below.
m for the first 200 s. The values of the relevant constants, which were retrieved from [12] -[16] , used are listed in Table 1 below.
4.1. Comparison at ![]() m and
m and ![]() m
m
We will first compare the models at a point that is close to the source of the nanoparticles, ![]() m. The bold graphs in Figure 2 and Figure 3 represent the exact results from [9] . As we can see from the graphs below, the shape of the graphs is slightly different. This change can be attributed to the fact that the flow velocity now depends on density, which now depends on the local concentration of the nanoparticles. So, as the concentration increases, the velocity will decrease, which explains why the concentration grows slower as time passes in the new model. A similar process can be used to explain why the graph decreases slower as well.
m. The bold graphs in Figure 2 and Figure 3 represent the exact results from [9] . As we can see from the graphs below, the shape of the graphs is slightly different. This change can be attributed to the fact that the flow velocity now depends on density, which now depends on the local concentration of the nanoparticles. So, as the concentration increases, the velocity will decrease, which explains why the concentration grows slower as time passes in the new model. A similar process can be used to explain why the graph decreases slower as well.
We will now compare the models at a point that is farther away from the nanoparticle source, ![]() m. From the graphs below we see that there is a much larger discrepancy between the two models. One major reason for this is the fact that the concentration at this point is not very influenced by the source. Furthermore, any discrepancy from points closer to the source are now exemplified farther down. This situation thus reveals the true effect of the electromagnetic interactions that occur.
m. From the graphs below we see that there is a much larger discrepancy between the two models. One major reason for this is the fact that the concentration at this point is not very influenced by the source. Furthermore, any discrepancy from points closer to the source are now exemplified farther down. This situation thus reveals the true effect of the electromagnetic interactions that occur.
![]()
Table 1. Values of model parameters.
![]()
Figure 2. Comparison of simulations for MNM1D of colloid transport at 1 mm ionic strength at ![]() m.
m.
4.2. Graphical User Interface
To permit users to easily test the model, a graphical user interface (GUI) was created. This allows users to enter model parameters including physical characteristics of the system, affecting both the dispersion of the colloids and the electric field, and the particle-soil interaction kinetic coefficients. The GUI presents the colloidal con- centrations at both of the above positions, ![]() m and
m and ![]() m. Figure 4 and Figure 5 below are screenshots of the program at startup, one with default parameters mirroring those used in this study and another
m. Figure 4 and Figure 5 below are screenshots of the program at startup, one with default parameters mirroring those used in this study and another
![]()
Figure 3. Comparison of Simulations for MNM1D of Colloid Transport at 1mM Ionic Strength at ![]() m.
m.
![]()
Figure 4. Graphical user interface at startup.
with user-entered parameters.
4.3. Parameter Estimation
The kinetic coefficients in the description of the attachment and detachment phenomena determine the ionic strength of the colloids. Being able to estimate the values of these given experimental data would allow for approximating this characteristic of the groundwater that would ultimately help determine properties such as the mobility of radioactive isotopes in the system [17] . Thus, a parameter estimation algorithm was implemented for one of these parameters![]() . To test how accurate the estimation process was, some “noise” or random deviations, were added to the computed values of concentration outputed by the model to make it more rea-
. To test how accurate the estimation process was, some “noise” or random deviations, were added to the computed values of concentration outputed by the model to make it more rea-
listically represent experimental data. The accuracy and error were recorded for different magnitudes of noise, the results are shown in Figure 6 and Figure 7.
![]()
Figure 5. Graphical user interface with user parameters.
![]()
Figure 6. Parameter estimation ![]() values error.
values error.
![]()
Figure 7. Parameter estimation model error.
5. Conclusions and Future Work
In this work, a new enhanced model that incorporates non-constant flow velocity governed by the Darcy-Forch- heimer fluid model as well as influence of electromagnetic interactions using H-S equation has been studied. We were not only able to validate the results in the absence of these effects in comparsion to published work, but were also able to show that these non-constant flow velocity and electromagnetic effects impact the colloid concentrations. Two other contributions include the development of a parameter estimation strategy to extract parameters of interest by comparing the computed data against experimental data. In this paper, the experimental data was generated by adding different levels of “noise” to the computed data. Finally, a graphical user interface, that helps users to enter model parameters and obtain the colloidal concentrations in real-time, was also pre- sented. The software that has been developed through this work provides flexible infrastructure to evaluate the influence of parameters such as ![]() and
and ![]() on the nanoparticle cocentration. The GUI allows users to evaluate this influence. While we have used a finite difference algorithm, we hope to establish the stability of the method in a forthcoming paper. We also hope to study stochastic effects that may be created by the randomness of the parameters in the model and finally extend our current model to higher dimensions.
on the nanoparticle cocentration. The GUI allows users to evaluate this influence. While we have used a finite difference algorithm, we hope to establish the stability of the method in a forthcoming paper. We also hope to study stochastic effects that may be created by the randomness of the parameters in the model and finally extend our current model to higher dimensions.
The current paper does not include explicitly the interaction of colloidal particles with various contaminants that can exist in groundwater. In a forthcoming paper, we wish to enhance our model by including this interac- tion as colloidal particles are well-known to remediate contaminants because of their unique physiochemical properties. Understanding this interaction will also help us to investigate how the colloidal particles can be used in the removal of various groundwater contaminants including chlrorinated compounds, pesticides, heavy metals, nitrates, and explosives in water ([18] and references therein). This will help us to enhance our software that can be more widely used by various stakeholders.