1. Introduction
Coprimely packed rings were introduced by Erdo˘gdu for the first time in [1] . Al-Ani gave an analogous concept in modules [2] , that is, a proper submodule N of an R-module M which is called Coprimely Packed. If 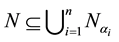 where
where 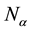 is a prime submodule of M for each
is a prime submodule of M for each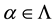 , then
, then 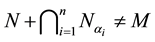 for some
for some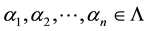 . If there exists
. If there exists  such that
such that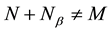 , then N is called Strongly Coprimely Packed submodule.
, then N is called Strongly Coprimely Packed submodule.
In this paper, we discuss the situation where the union of a family of primary submodules of M is considered.
In [2] , the concept of compactly packed modules was introduced. We generalized this concept to the concept of p-compactly packed modules in [3] , that is, a proper submodule N of an R-module M which is called
P-Compactly Packed. If for each family 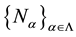 of primary submodules of M with
of primary submodules of M with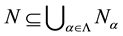 , there ex-
, there ex-
ist ![]() such that
such that![]() . If
. If ![]() for some
for some![]() , then N is called Strongly
, then N is called Strongly
P-Compactly Packed. A module M is said to be P-Compactly Packed (Strongly P-Compactly Packed), if every proper submodule of M is p-compactly packed (strongly p-compactly packed).
In this paper, we introduce the definitions of coprimarily packed and strongly coprimarily packed module and discuss some of their properties. We end this paper by explaining the relations between p-compactly packed and coprimarily packed submodules, and also the relations between strongly p-compactly packed and strongly coprimarily packed submodules.
2. Coprimarily Packed and Strongly Coprimarily Packed Submodules
In this section we introduce the definition of coprimarily packed and strongly coprimarily packed module and discuss some of their properties.
2.1. Definition
Let N be a proper submodule of an R-module M. N is said to be Coprimarily Packed Submodule if whenever ![]() where
where ![]() is a primary submodule of M for each
is a primary submodule of M for each![]() , then
, then ![]() for some
for some![]() . When there exists
. When there exists ![]() such that
such that![]() , N is called Strongly Coprimarily Packed submodule.
, N is called Strongly Coprimarily Packed submodule.
A module M is called Coprimarily Packed (Strongly Coprimarily Packed) module if every proper submodule of M is coprimarily packed (strongly coprimarily packed) submodule. It is clear that every strongly coprimarily packed submodule is a coprimarily packed submodule.
In the following proposition, we discuss the behavior of strongly coprimarily packed module under homomorphism.
2.2. Proposition
Let ![]() be an epimorphism. If M is an R-module such that
be an epimorphism. If M is an R-module such that ![]() for every primary submodule N of M, then M is a strongly coprimarily packed module if and only if
for every primary submodule N of M, then M is a strongly coprimarily packed module if and only if ![]() is a strongly coprimarily packed module.
is a strongly coprimarily packed module.
Proof. Suppose that M is a strongly coprimarily packed module and let ![]() where
where ![]() is a proper submodule of
is a proper submodule of ![]() and
and ![]() is a primary submodule of
is a primary submodule of ![]() for each
for each![]() , so
, so
![]() .
.
![]() is a primary submodule of M for each
is a primary submodule of M for each ![]() there exists
there exists ![]() such that
such that
![]() .
.
We must show![]() .
.
Suppose![]() , let
, let ![]() so there exists
so there exists ![]() and
and ![]() such that
such that![]() . Since f is an epimorphism there exists
. Since f is an epimorphism there exists ![]() such that
such that
![]() ,
,![]() , and
, and![]() .
.
Thus![]() , so
, so![]() , this implies
, this implies![]() . Since
. Since![]() ,
,
![]() , and
, and![]() , so
, so![]() , hence
, hence
![]() ,
,
this implies
![]()
which is a contradiction. So ![]() is a strongly coprimarily packed module.
is a strongly coprimarily packed module.
Conversely, suppose ![]() is a strongly coprimarily packed module and let
is a strongly coprimarily packed module and let![]() , where N is a proper submodule of M and
, where N is a proper submodule of M and ![]() is a primary submodule of M for each
is a primary submodule of M for each![]() . Hence
. Hence
![]()
and since ![]() for each
for each![]() ,
, ![]() is a primary submodule of
is a primary submodule of![]() , there exists
, there exists ![]() such that
such that![]() .
.
Suppose ![]() and let
and let![]() , since f is an epimorphism, there exists
, since f is an epimorphism, there exists ![]() such that
such that ![]() and there exists
and there exists ![]() and
and ![]() such that
such that![]() . Then
. Then![]() , hence
, hence![]() , so
, so![]() ). It follows
). It follows ![]() which is a contradiction, thus
which is a contradiction, thus![]() , so M is a strongly coprimarily packed modul.
, so M is a strongly coprimarily packed modul.
The following proposition gives a characterization of strongly coprimarily packed submodules in a multiplication or finitely generated module.
2.3. Proposition
Let M be a finitely generated or multiplication R-module. A proper submodule N is strongly coprimarily packed if and only if whenever ![]() where
where ![]() is a maximal submodule of M for each
is a maximal submodule of M for each ![]() then there exists
then there exists ![]() such that
such that![]() .
.
Proof. Suppose N is a strongly coprimarily packed submodule and let ![]() where
where ![]() is a maximal submodule of M for each
is a maximal submodule of M for each![]() , hence
, hence ![]() is a primary submodule, so there exists
is a primary submodule, so there exists ![]() such that
such that![]() . But
. But ![]() and
and ![]() is a maximal submodule, hence
is a maximal submodule, hence ![]() thus
thus![]() .
.
Conversely, let ![]() where
where ![]() is a primary submodule for each
is a primary submodule for each![]() . There exists a maximal submodule
. There exists a maximal submodule ![]() that contains
that contains ![]() for each
for each![]() , hence
, hence![]() . By hypothesis, there ex- ists
. By hypothesis, there ex- ists ![]() such that
such that![]() , but
, but ![]() so
so![]() , thus N is a strongly coprimarily packed submodule.
, thus N is a strongly coprimarily packed submodule.
Recall that an R-module M is called Bezout Module if every finitely generated submodule of M is cyclic.
In the following proposition we will give a characterization for strongly coprimarily packed multiplication module.
2.4. Proposition
Let M be a multiplication R-module. If one of the following holds:
1) M is a cyclic module.
2) R is a Bezout ring.
3) M is a Bezout module.
Then M is strongly coprimarily packed module if and only if every primary submodule is strongly coprimarily packed.
Proof. Let N be a proper submodule of a module M such that ![]() where
where ![]() is a maximal submodule of M for each
is a maximal submodule of M for each![]() , then by proposition (2.3), it is enough to show that there exists
, then by proposition (2.3), it is enough to show that there exists ![]() such that
such that![]() .
.
First, if![]() , since N is a submodule of a multiplication module, there exists a primary submodule L that contains N. By hypothesis, L is strongly coprimarily packed submodule and
, since N is a submodule of a multiplication module, there exists a primary submodule L that contains N. By hypothesis, L is strongly coprimarily packed submodule and![]() , so there exists
, so there exists ![]() such that
such that ![]() hence
hence![]() .
.
Now, if![]() , let
, let ![]() and
and![]() , so
, so ![]() is an
is an ![]() -closed subset of M. Since
-closed subset of M. Since![]() , so
, so ![]() thus there exists a submodule K that contains N and K is a maximal in
thus there exists a submodule K that contains N and K is a maximal in ![]() [1] , K is prime [1] , so it is primary submodule. Thus by hypothesis K is strongly coprimarily packed and since
[1] , K is prime [1] , so it is primary submodule. Thus by hypothesis K is strongly coprimarily packed and since ![]() and by proposition (2.3) there exists
and by proposition (2.3) there exists ![]() such that
such that![]() .
.
We end this Paper by looking at the relations between the strongly p-compactly packed modules and strongly coprimarily packed modules.
Recall that a proper submodule N of an R-module M is called P-Compactly Packed if for each family ![]()
of primary submodules of M with![]() , there exist
, there exist ![]() such that
such that![]() . If
. If
![]() for some
for some![]() , then N is called Strongly P-Compactly Packed. A module M is said to be P-Com- pactly Packed (Strongly P-Compactly Packed) if every proper submodule of M is p-compactly packed (strongly p-compactly packed).
, then N is called Strongly P-Compactly Packed. A module M is said to be P-Com- pactly Packed (Strongly P-Compactly Packed) if every proper submodule of M is p-compactly packed (strongly p-compactly packed).
It is easy to show that every strongly p-compactly packed submodule is a strongly coprimarily packed submodule.
2.5. Proposition
If M is a p-compactly packed module, which cannot be written as a finite union of primary submodules, then M is a coprimarily packed module.
Proof. Let ![]() where N is a proper submodule and
where N is a proper submodule and ![]() is a primary submodule of M for each
is a primary submodule of M for each![]() . Since M is a p-compactly packed module then there exists
. Since M is a p-compactly packed module then there exists ![]() such that
such that![]() .
.
We claim that![]() , let
, let ![]() so there exists
so there exists ![]() and
and ![]() such that
such that![]() . Then there exists
. Then there exists ![]() such that
such that![]() , hence
, hence![]() , so
, so![]() , thus
, thus
![]() .
.
By hypothesis ![]() therefore
therefore![]() .
.
2.6. Definition
Let M be a non-zero module, M is called Primary Module if the zero-submodule of M is a primary submodule.
2.7. Proposition
If M is a multiplication or finitely generated strongly p-compactly packed module, then M is a strongly coprimarily packed module. The converse holds if M is a primary module such that every primary submodule of M contains no non-trivial primary submodule.
Proof. Suppose M is a primary module such that every primary submodule of M contains no non-trivial primary submodule. Let N be a proper submodule of M such that ![]() where
where ![]() is a primary submodule of M for each
is a primary submodule of M for each![]() . Without loss of generality we can suppose that
. Without loss of generality we can suppose that![]() , for each
, for each![]() . Then
. Then ![]() is a maximal submodule of M, for each
is a maximal submodule of M, for each![]() . Since M is strongly coprimarily packed module, there exists
. Since M is strongly coprimarily packed module, there exists![]() , such that
, such that![]() ; but
; but ![]() is a maximal submodule and
is a maximal submodule and![]() . This implies
. This implies![]() , and hence
, and hence![]() . Therefore M is a strongly p-compactly packed module.
. Therefore M is a strongly p-compactly packed module.
The other direction is trivial.