Torsional Behavior Design of UHPC Box Beams Based on Thin-Walled Tube Theory ()
1. Introduction
Ultra high performance concrete (UHPC) is an advanced cementitious composite exhibiting low permeability in which the matrix with high density and strength is reinforced by steel fibers [1] -[4] . This composite develops significantly higher tensile strength than ordinary concrete [5] and continues to show outstanding behavior after cracking [3] [6] . However, despite of its remarkable strength and performances compared with normal strength concrete (NSC), this material is still costly. Accordingly, the structures applying UHPC present often more complicated shapes and reduced cross sectional dimensions than when applying NSC. This situation stresses the importance of the torsional design of UHPC structures.
Studies reported that the design of torsional reinforcement focused essentially on stirrups by disregarding the tensile behavior of concrete in the case of NSC structures [7] [8] . Other studies were also dedicated to the tor- sional behavior of prestressed NSC structures [9] . Several studies also considered the torsional behavior of structures made of high strength concrete (HSC) without steel fiber reinforcement [10] -[15] . However, HSC shows poor torsional ductility, and offers very narrow reinforcement ratio enabling to preserve the ductility [15] ; and the torsional cracks are more brittle than in NSC [13] .
Many researchers led investigation on the improvement of the tensile strength and ductility of NSC by steel fiber reinforcement and found out that the adoption of steel fiber achieved improved flexural ductility and ten- sile strength [16] -[18] as well as significant amelioration of the shear strength [19] [20] . Further studies also re- ported the effectiveness of steel fiber in improving the torsional behavior [21] -[26] .
The remarkable ductile behavior of UHPC can also be attributed to the steel fiber reinforcement. This feature must be considered to provide rational explanation of the torsional behavior of UHPC structures. The current design specification of ACI 318-11 describes the torsional design of structures based upon the thin-walled tube theory [27] , but its straightforward application to UHPC cannot consider properly the effect resulting from the improvement of the ductile behavior of UHPC identified experimentally. Accordingly, the torsional design me- thod of the UHPC beam shall be based on a modified theory enabling to account for the tensile behavior of UHPC rather than the traditional theory.
In this study, the proposed torsional design adopts a modified thin-walled tube theory so as to consider the tensile behavior of UHPC and the validity of the method is verified through comparison with experimental data. Most of the recent studies on UHPC focused only on the difference in the constitutive materials as compared with normal concrete. Despite of the insufficiency of experimental research utilizable for the analysis of the tor- sional behavior of UHPC beams, Yang, Joh, Lee and Kim conducted the experimental analysis of the pure tor- sional behavior of UHPC beams with rectangular cross-section [28] .
Accordingly, this experimental study intends to propose a torsional design method based on the thin-walled tube theory and considering the tensile strength of UHPC. UHPC beams with thin-walled box cross-section were fabricated and subjected to pure torsion test for comparison with the theoretical data and to verify the validity of the proposed design method.
2. Torsional Design Based on Thin-Walled Theory
In order to obtain the ultimate strength of the UHPC beam considering the tensile behavior of UHPC, the beam undergoing cracking due to the torsional moment T is idealized as a thin-walled tube (Figure 1).
![]()
Figure 1. Thin-wall tube model UHPC beam.
The total shear forces  and
and 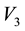 at the top and bottom flanges of the box beam caused by the torsional moment
at the top and bottom flanges of the box beam caused by the torsional moment 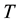 shown in Figure 1 can be expressed as follows,
shown in Figure 1 can be expressed as follows,
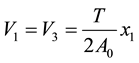 (1)
(1)
and, the total shear forces 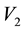 and
and  in both webs can be expressed as follows in a similar manner,
in both webs can be expressed as follows in a similar manner,
 (2)
(2)
where  area delimited by the centerline of the shear flow;
area delimited by the centerline of the shear flow;  width of
width of ; and,
; and,  height of
height of .
.
The number of stirrups including the inclined crack surface at the leftward face of the UHPC beam (Figure 2) in which torsion-induced cracks occurred is obtained by Equation (3).
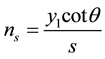 (3)
(3)
where 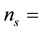 number of stirrups including the inclined crack surface;
number of stirrups including the inclined crack surface; 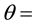 inclination angle of compression strut; and,
inclination angle of compression strut; and, ![]() spacing of closed stirrup.
spacing of closed stirrup.
Figure 2 shows vertical forces resulting from tensile strength of UHPC ![]() acting on a crack surface with inclination angle
acting on a crack surface with inclination angle ![]() and tensile strength of stirrups.
and tensile strength of stirrups. ![]() stands for the cross-sectional area of one closed stirrup resisting to torsion within spacing s.
stands for the cross-sectional area of one closed stirrup resisting to torsion within spacing s.
Accordingly, assuming that all the stirrups yield at ultimatetorsion limit state and that UHPC reaches its ten- sile strength![]() , the contribution
, the contribution ![]() to the shear force
to the shear force ![]() of the stirrup can be calculated as follows,
of the stirrup can be calculated as follows,
![]() (4)
(4)
where ![]() yield strength of transverse reinforcement.
yield strength of transverse reinforcement.
Moreover, Equation (5) expresses the tensile force of UHPC acting vertically to the inclined crack surface of Figure 2.
![]() (5)
(5)
where ![]() tensile strength of UHPC; and,
tensile strength of UHPC; and, ![]() thickness of thin wall when assuming the UHPC beam as equivalent thin-walled tube for torsional strength.
thickness of thin wall when assuming the UHPC beam as equivalent thin-walled tube for torsional strength.
Therefore, the vertical component in Equation (5) that is the contribution ![]() to the shear force
to the shear force ![]() of UHPC can be expressed as follows
of UHPC can be expressed as follows
![]()
Figure 2. Vertical forces in leftward face of UHPC thin-walled tube models.
![]() (6)
(6)
Consequently, the total shear force ![]() acting on the leftward face of the beam can be obtained by Equation (7).
acting on the leftward face of the beam can be obtained by Equation (7).
![]() (7)
(7)
In addition, the corresponding torsional moment ![]() is the ultimate torsional moment
is the ultimate torsional moment ![]() that can be sus- tained by the section, and can be obtained as follows based on Equations (7) and (2).
that can be sus- tained by the section, and can be obtained as follows based on Equations (7) and (2).
![]() (8)
(8)
By distinguishing the contributions of the steel reinforcement and UHPC, Equation (8) becomes
![]() (9)
(9)
The cracking torque ![]() can also be obtained consistently by applying the thin-walled beam theory. In other words, the shear stress
can also be obtained consistently by applying the thin-walled beam theory. In other words, the shear stress ![]() at which inclined cracks initiate at one side of the UHPC beam under the action of the cracking torque
at which inclined cracks initiate at one side of the UHPC beam under the action of the cracking torque ![]() can be calculated as follows.
can be calculated as follows.
![]() (10)
(10)
where ![]() thickness of UHPC beam assumed as equivalent thin-walled tube.
thickness of UHPC beam assumed as equivalent thin-walled tube.
Moreover, if the member transverse compressive stress ![]() induced by prestress applies, the principal stress
induced by prestress applies, the principal stress ![]() can be obtained using the Mohr’s circle shown in Figure 3 [29] . Here, the compressive stress
can be obtained using the Mohr’s circle shown in Figure 3 [29] . Here, the compressive stress ![]() must be positive considering the sign convention.
must be positive considering the sign convention.
![]() (11)
(11)
If this principal stress ![]() becomes equal to the crack strength
becomes equal to the crack strength ![]() of UHPC, the shear stress
of UHPC, the shear stress ![]() developed in one side of the UHPC beam becomes
developed in one side of the UHPC beam becomes ![]() inducing inclined cracks. Therefore, Equation (11) can be rewrit- ten as follows for
inducing inclined cracks. Therefore, Equation (11) can be rewrit- ten as follows for![]() .
.
![]() (12)
(12)
Hence, the cracking torque ![]() can be obtained as follows from Equations (10) and (12).
can be obtained as follows from Equations (10) and (12).
![]()
Figure 3. Principal stress of prestressed torsional member [29] .
![]() (13)
(13)
In addition, the inclination angle ![]() of the inclined crack can be expressed as follow using the Mohr’s circle.
of the inclined crack can be expressed as follow using the Mohr’s circle.
![]() (14)
(14)
3. Test Schedule
3.1. Material Characteristics
Ordinary Portland cement is used in the mix of steel fiber reinforced UHPC, and reactive powder and silica fume are also introduced. A water-to-binder of 0.2% is applied. Sand with grain size of 0.5 mm is used as fine aggregate, and coarse aggregate is not used. The filler is made of materials with average grain size of 10 μm, SiO2 content larger than 98% and density of 7500 kg/m3. Straight steel fiber is adopted with density of 7500 kg/m3, yield strength of 2500 MPa and diameter of 0.2 mm. Two fiber lengths of 16.5 mm and 19.5 mm are used concurrently at volume fractions of 1% and 1.5%.
Series of 6 specimens for tensile strength test were fabricated at each batch during the manufacture of the beam member using the placed UHPC. Direct tensile test was conducted to evaluate the tensile strength of each specimen. The dogbone type tensile specimens shown in Figure 4 were notched on both side of their center to a depth 12.5 mm. Crack gages were used to measure the crack mouth opening displacement (CMOD) of the notch according to the increase of the tensile load so as to compute the crack initiation strength and tensile strength of each specimen. Table 1 arranges the average values calculated for the specimens of each batch.
3.2. Test Members
The test members were fabricated with rectangular box cross-section and dimensions of 350 mm ´ 350 mm ´ 3000 mm. For the tested part of the member, the central part (section B-B) was designed to have a wall thick- ness of 50 mm to induce torsional failure. To that goal, both ends of the member (section A-A) were designed with wall thickness of 120 mm, dense arrangement of D10 stirrups at spacing of 50 mm along a length of 650 mm, and the installation of 3 longitudinal reinforcements in each side of the rectangular cross-section. Moreover, apart from the ends of the member, D10 stirrups were disposed in section B-B along the member at spacing of 170 mm or 340 mm.
![]()
Figure 4. Dogbone UHPC specimen for direct tensile test.
For the members with prestress, nineteen 7-wire tendons with nominal diameter of 15.2 mm (SWPC7, yield strength of 1860 MPa) were installed at the center of the empty box of the member.
A total of 14 test members corresponding to 2 specimens for each of 7 types were fabricated considering the test variables that are the volume fraction of steel fiber (1.0%, 1.5%), the amount of stirrups and reinforcing steel, and the introduction of prestress. Table 2 arranges the characteristics of the specimens. Figure 5 and Figure 6 illustrate the cross-sections and side view of the UHPC box beam members. As shown Figure 5 and Figure 6, section A-A in both side of box beams was heavily reinforced with large number of stirrups and thick UHPC wall so as to protect occurrence of diagonal cracks in those region.
![]()
Table 1. Tensile strength of UHPC torsion specimens (MPa).
![]()
Table 2. Dimensions of UHPC beam specimens for torsion test (mm).
![]()
Figure 5. Cross-section of UHPC box beam specimen.
3.3. Test Method
The torque was applied as shown in Figure 7 using an actuator with capacity of 1000 kN. The torsional moment lever arm was 0.9 m and the torsional load was applied at the 2.3 m spot of the 3 m long box beam specimens. One support of the member was fixed to restrain rotation while the other support was installed with an arc bear- ing to allow free rotation in the transverse direction.
For the prestressed member, a hydraulic jack for the introduction of the prestress force in the tendon and a load cell for the measurement of the prestress force were installed in series at the fixed end of the member as shown in Figure 8(a) and Figure 8(c). Moreover, at the hinged end, a spherical roller trust bearing with vertical capacity of 600 ton was installed in series between the anchor plate for the tendon and the end of the member as shown in Figure 8(b). This roller was installed to prevent the risk of damage of the tensioned tendons inside the member box due to twisting or change in the axial load under the rotation of the beam. Different amounts of prestress were applied as 0.0 MPa, 12.5 MPa, 25.0 MPa, and 50.0 MPa according to the test member, and the corresponding behavioral change was observed through the crack inclination and torsional strength.
A loading beam was installed at the rotating support. The load was applied at the position of the loading lo- cated at a distance of 0.9 m from the centerline of the member, which corresponds to the lever arm. Loading was applied through displacement control at speed of 0.03 mm/s. The rotating end was fabricated considering the ro- tation radius with respect to the centerline of the member.
The observation of the torsional angle or angle of twist of the beam was done by measuring the deflection at each loading stage using steel frames and LVDTs installed at sections located at 800 mm and 200 mm far from the center of the span as shown in Figure 9.
![]()
Figure 6. Side elevation view of UHPC box beam specimen.
![]()
![]() (a) Schematic drawing (b) View of test setup
(a) Schematic drawing (b) View of test setup
Figure 7. Schematic drawing of test configuration and view of test setup.
![]()
Figure 9. Layout of displacement gauges.
4. Test Results and Discussion
4.1. Crack Characteristics
The propagation of the cracks was observed at each loading stage until failure, and the relation between the tor- sional moment-angle of twist was measured. Table 3 arranges the inclination angle of the cracks measured with reference to the centerline of the member at the initiation of crack.
Initial cracking occurred in the form of inclined cracks with inclination angles ranging between 46.7˚ and 51.3˚ with reference to the centerline of the beam in the specimens without prestress, which gives an average angle of 49.7˚. For the prestressed members, the crack angles diminished gradually with larger longitudinal prestress to range between 14˚ and 15˚ in the case of the peak prestress of 50 MPa as shown in Figure 10(a).
After the initiation of the torsional cracks, the cracks exhibited spiral shape along the 4 sides of the members according to the increase of the torsional moment together with the occurrence of numerous torsional cracks. These additional cracks seem to enhance the load bearing capacity of the member owing to the redistribution of stress. Just prior to the peak torsional moment, some specific cracks among the inclined cracks showed increase of their crack width and developed into principal inclined cracks. After the peak load, the torsional moment re- duced with the acceleration of the pullout of the steel fibers and failure occurred as shown in Figure 10(b) with the sudden widening of the crack width of the principal inclined cracks. This process can be explained by the in- creased resistance to torsional moment provided by the bridging effect of the steel fibers from the initiation of cracks to the ultimate loading stage and, the loss of this resistance after the ultimate load due to the reduction of
![]()
Table 3. Crack inclination of UHPC beam specimens.
![]()
![]() (a) Crack growth stage (SH-P4-F1-L1-S1) (50 MPa prestress) (b) Ultimate failure stage (SH-P0-F1-L1-S1(D13))(0 MPa prestress)
(a) Crack growth stage (SH-P4-F1-L1-S1) (50 MPa prestress) (b) Ultimate failure stage (SH-P0-F1-L1-S1(D13))(0 MPa prestress)
Figure 10. Representative cracking patterns of torsional member.
the bridging effect of the steel fibers at the principal inclined cracks. Similar crack propagation and failure pattern were observed in previous experimental studies on rectangular plain UHPC beams [28] .
4.2. Torsional Strength Characteristics according to the Change of Reinforcement
Figure 11 plots the relation between the torsional moment and the angle of twist measured in the non-prestressed members. At early loading, the relation is nearly linear. With the increase of the volume fraction of steel fiber from 1.0% to 1.5%, the maximum torsional moment undergoes clear increase from 76.4 kN-m and 84.9 kN-m for member SH-P0-f1.0-L1-S1(D13) to 96.6 kN-m and 100.7 kN-m for member SH-P0-f1.5-L1-S1(D13).
In the case where the longitudinal reinforcement is increased from 4 D-10 bars to 4 D-13 bars, the peak tor- sional moment is seen to vary from 104.6 kN-m and 87.2 kN-m for member SH-P0-f1.5-L1-S1(D10) to 96.6 kN-m and 100.7 kN-m for member SH-P0-f1.5-L1-S1(D13). This means that the increase of the longitudinal reinforcement has no effect on the increase of the torsional resistance.
For the transverse reinforcement, when the number of stirrups is doubled, the peak torsional moment is seen to change from 104.6 kN-m and 87.2 kN-m for member SH-P0-f1.5-L1-S1(D10) to 97.5 kN-m and 104.7 kN-m for member SH-P0-f1.5-L1-S2(D10). This indicates that, for the members considered in this study, the increment in the torsional resistance resulting from the increase of the stirrups is smaller than that resulting from the increase of the steel fiber content. Besides, the increase of the stirrups is seen to augment the ductility in the torsional mo- ment-angle of twist relation owing to the generation of a larger number of inclined cracks favoring the redistribu- tion of stress.
The change in the peak torsional moment according to the increase of the amount of steel fiber, increase of transverse reinforcement, and increase of longitudinal reinforcement is similar to that observed by Yang, Joh, Lee and Kim in their experimental study on UHPC beams with plain rectangular cross-section [28] .
Figure 12 plots the relation between the torsional moment and the angle of twist measured in the prestressed members. The torsional resistance is seen to increase significantly according to the amount of prestress. The peak torsional moment of member SH-P4-f1.5-L1-S1-1 with prestress of 12.5 MPa is 145.8 kN-m and becomes 190.6 kN-m and 187.9 kN-m for the two SH-P4-f1.5-L1-S1 members and 192.0 kN-m for member SH-P4-f1.5-L1-S1-2 with prestress of 25.0 MPa. However, brittle failure occurred after the peak value as compared to the cases with- out prestress.
![]()
Figure 11. Torsional moment-angle of twist curve (torsional members without prestress).
![]()
Figure 12. Torsional moment-angle of twist curve (torsional members with prestress).
Moreover, the peak torsional moment of member SH-P4-f1.0-L1-S1-2 with prestress of 50.0 MPa is 212.8 kN-m. This indicates the larger increase of the peak torsional moment even with a small steel fiber volume frac- tion of 1.0% compared to the case with small prestress and steel fiber volume fraction of 1.5%. For example, the identical member SH-P4-f1.0-L1-S1-1, which underwent reduction of its prestress force due to the dysfunction of the hydraulic jack during the jacking of the prestressing tendon, resisted only up to a peak torsional moment of 167.5 kN-m.
4.3. Comparative Analysis with the Results Predicted by Design Formula
Table 4 compares the values of the cracking torque ![]() and ultimate torsional moment
and ultimate torsional moment ![]() obtained experi- mentally and predicted analytically using Equations (13) and (9). The ultimate torsional moments computed using the calibrated
obtained experi- mentally and predicted analytically using Equations (13) and (9). The ultimate torsional moments computed using the calibrated ![]() of the inclination angle and using the non-calibrated value of
of the inclination angle and using the non-calibrated value of ![]() are both used for the com- parison.
are both used for the com- parison.
For the cases without prestress, the inclined cracks should theoretically form an angle of 45˚ with the centerline of the member. However, slight deviation was reported in the observation of the shear test of beam members. Therefore, the value of the inclination angle ![]() is calibrated to correct this deviation. The Japanese provisional design guidelines for UHPC adopt a deviation of 5˚ for
is calibrated to correct this deviation. The Japanese provisional design guidelines for UHPC adopt a deviation of 5˚ for ![]() based on previous experimental data [30] . In the present study, an average deviation of 4.7˚ from the line inclined by 45˚ to the centerline of the beam was observed for the inclined cracks identified in the 8 members without prestress (Table 3).
based on previous experimental data [30] . In the present study, an average deviation of 4.7˚ from the line inclined by 45˚ to the centerline of the beam was observed for the inclined cracks identified in the 8 members without prestress (Table 3).
Figures 13 compares the analytic and experimental values of the cracking torque![]() . And Figure 14 and Figure 15 compare the analytic and experimental values of the ultimate torsional moment
. And Figure 14 and Figure 15 compare the analytic and experimental values of the ultimate torsional moment ![]() of the UHPC beam members tested in this study. Figure 14 does not account the calibrated value
of the UHPC beam members tested in this study. Figure 14 does not account the calibrated value ![]() of the inclination angle whereas Figure 15 considers
of the inclination angle whereas Figure 15 considers ![]() for
for![]() .
.
5. Conclusions
This study proposed a prediction formula for the torsional strength enabling to reflect the tensile strength of ultra high performance concrete (UHPC) beams based upon the thin-walled tube theory. Torsion test was conducted on thin-walled UHPC box beams to validate the proposed formula through comparison of the predicted torsional
![]()
Table 4. Comparison of experimental and predicted cracking torque (Tcr) and ultimate torsional moment (Tn).
![]()
Figure 13. Comparison of analytic and experimental crack- ing torque Tcr.
![]()
Figure 14. Comparison of analytic and experimental ultimate torsional moment Tn (θ0 not accounted).
![]()
Figure 15. Comparison of analytic and experimental ultimate torsional moment Tn (θ0 accounted).
strength with the experimental results. The following conclusions can be drawn.
1) The thin-walled tube theory was adopted to derive the prediction formula of the torsional strength so as to reflect the contribution of the tensile strength of UHPC provided by the steel fibers to the torsional strength of the beam. The comparison of the predicted values of the cracking torque and torsional moment resistance with those observed in the torsional test of UHPC verified the validity of the design method.
2) The observation of the cracking and failure patterns revealed the occurrence of several additional inclined cracks after the initial cracks according to the increase of the load. The members exhibited post-cracking behavior with continuous increase of the load until the ultimate limit state. This indicated that the torsional behavior of the UHPC beams developed clear ductility owing to the steel fibers even after the initiation of cracks. However, the prestressed members showed brittle failure after the peak load.
3) The contribution of the steel fibers to the torsional strength and cracking load was larger than that of the stirrups, but the stirrups appeared to contribute additionally to the torsional ductility. Accordingly, it is recom- mended that design should exploit effectively the contribution of the steel fiber rather than arrange a larger num- ber of stirrups in UHPC structures subjected to torsion.
4) An average deviation of 4.7˚ from the theoretical angle of 45˚ predicted for the inclined cracks in the case of beam members without prestress. The consideration of this deviation enabled the prediction to approach more accurately the experimental data. The inclination angle of the inclined cracks reduced and the ultimate torsional strength increased with larger amount of prestress. Since the torsional resistance varied more sensitively to the change in the angle of the torsional cracks with larger prestress, attention should be paid on the computation of the crack angle in the design.
Acknowledgements
This research was supported by a grant (14 AUDP-B069364-02) from Urban Architectural Research Program funded by Ministry of Land, Infrastructure and Transport of Korean Government.
NOTES
*Corresponding author.