Computational Analysis of Anastomotic Angles by Blood Flow Conditions in Side-to-End Radio-Cephalic Fistulae Used in Hemodialysis ()
1. Introduction
Chronic renal failure is a disease in which partial loss of the kidney function occur in a slow, progressive and irreversible way. As a leading alternative treatment for this deficiency, the blood filtering process called hemodialysis is used. This is a process which consists in filtering blood and removing impurities from this fluid, similar to the process executed by the kidney. The blood is first transported through a venous access connected to an artificial arterial fistula and subsequently the blood passes through the dialysis process being filtered [1] . In this case, the chronic renal failure patient may undergo various disorders such as nausea and loss of venous access, among others.
The problems related to fistulae are believed to be caused due to friction generated by the shear forces of blood on the vessel walls, causing diseases like intimal hyperplasia and thrombosis [2] [3] .
Intimal hyperplasia is a process in which cells proliferate on the vessel walls in response to injury. This can reduce the diameter of the vessels, obstructing the passage of blood, and can lead to blood clotting [4] [5] forming stenoses. The main region of stenosis formation generated by hyperplasia is near the junction of the vein or graft and the main vessel, generally an artery, causing failure in the maturation of vascular grafts for hemodialysis [6] . One of the most widely used vascular access is the junction between the radial artery and the cephalic vein known as radio-cephalic fistula, arranged mostly in two different configurations known as end-to-end and side-to-end anastomoses. These junctions suffer constantly with the development of stenoses [7] .
Endothelial cells are sensitive to wall shear stress and in oscillatory flows these cells and those within the flowing blood are subjected to a wide range of varying shear stress. Both high and low shear influence the ways these cells respond to local hemodynamic conditions. There is a propensity to develop stenoses at specific sites, suggesting that the geometry of the fistula and the resulting local hemodynamic conditions have their role in the development of that disease [8] .
In vascular vessels, shear stress acts mainly on the inner surface of the vessels wall (endothelium) and has an indirect function to regulate vessel diameter. Following [9] , high levels of shear increases wall thickness and expand vessel diameters, and low shear stresses induces reduction in vessel diameters leading to intimal hyperplasia and other pathologies [10] [11] . Studies relating shear stress and endothelium responses suggest that normal, relative high, levels of shear stress also stimulates endothelium to release antithrombotic biochemical agents [12] - [17] . [18] performed in vitro investigations of cell responses from cultured endothelium cells subjected to simple shear flows and, among many other enlightening conclusions, the authors reported the bad association between oscillating and low levels of shear stress, and regions with disturbed flows were associated with local accumulation of LDL cholesterol.
According to several researches, low shear stresses are accompanied by unstable fluid conditions like turbulence, stagnation regions, recirculation and are related to several pathologies [19] [20] . Atherogenesis in arteries has been identified in association with low shear stresses by [3] [19] - [23] . Low shear stress levels have been associated to anastomosis, thrombosis and intimal hyperplasia in grafts [6] , and to in-stent restenosis [24] . Progressive plaques and vascular remodeling have been related to low shearing regions in an in vivo study of coronary artery by [25] , and to oscillating shear stress by [26] .
[27] investigated flow conditions in end-to-end fistulae accesses used in hemodyalisis, considering Carreau model for blood. In [2] analyses of radial-cephalic fistulae have been carried out for three configurations: end- to-end, side-to-end with antegrade and retrogate flow for a fixed anastomotic angle.
Aiming the suitability of minimally invasive techniques, computational models capable of simulating blood behavior are being widely required. Considering computational fluid dynamics, [28] performed simulations analyzing and indicating disturbed flow conditions in association with shear stress in carotid bifurcation for large vessel Newtonian blood model. Wall shear-stress and flow distribution have been computationally investigated by [29] in cerebral aneurisms. In [2] , radial-cephalic fistulae for three conformations were analyzed: end- to-end, side-to-end with antegrade and retrogate flow for a fixed anastomotic angle. In [30] they were simulated anastomotic angles of 30˚, 40˚, 60˚ and 90˚ using Carreau model and, from the results for velocity and relative residence time, conclusions have been reported in favor of the smaller angle.
In this work, aiming to contribute to the investigation of better anatomical configurations that could generate more favorable hemodynamic conditions, to minimize the problems related with fistulae failures, computational analyses are performed considering six medium to small anastomotic angles: 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚, before any stenosis or other pathologies have started. In this case, the vessel diameters are big enough (>0.1 mm) to consider large vessel Newtonian blood flow model [31] -[35] . A finite volume computational method is used to solve the equations for the pulsating flow problems, using as a basis the OpenFoam free software platform. To analyze the possibility of stenosis formation, results are obtained here for wall shear stress, oscillatory index, velocity contour fill and local circulation fields. From the results, a narrow range around 25˚ is suggested as the most suitable choice for clinical applications, minimizing possibilities of diseases.
2. Methodology
2.1. Geometrical Model
3-D arteriouvenous radial-cephalic side-to-end fistulae with antegrade blood flow are considered here. Straight arteries of length 15.0 cm and 3.1 mm diameter; vein of length 10.0 cm and 4.01 mm of diameter, with anastomotic angles of 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚ will be studied. In Figure 1, inlet and outlets are identified by i and o, respectively, and arrows indicate the directions of the flow at those locations.
At the artery inlet section, a pulsating velocity condition will be prescribed and at the outlets a developed flow condition will be considered.
2.2. Mathematical Model for the Flow
Blood is very well known to be a suspension of several components, large and small ones, in almost Newtonian liquid called plasma, and is, in essence, a non-Newtonian fluid in the sense that it is able to alter its structure and adapt itself behaving differently depending on where it is flowing in. These differences come out depending on several factors, being very evident if blood is flowing in large or in small vessels. In normal large vessels (without stenosis, etc.), (diameters > 0.1 mm) Reynolds numbers are high enough to preclude aggregation of red cells (RBC) and Womersley numbers (Wo) are high, characterizing the pulsating effects to be considerable, [31] [32] [35] [36] , but viscosity independent of the shear rate for a fixed hematocrit, characterizing Newtonian behavior. Differently, in small vessels Reynolds numbers are smaller than 1, pulsation is negligible (Wo < 1) and diverse non-Newtonian behaviors come out with viscosity being a function of the shear rate due to the key cell aggregation process which involves protein content, platelets action, varying particle concentration, and other factors [32] [33] [36] - [39] . Several constitutive equations have been proposed in order to describe non-Newtonian behavior of blood, none of them being the general one and experiments supply the constitutive parameters from viscometric flows. In the classical biomechanics of fluids, accounting for large and small vessel diameters (d), hemodynamic is divided into macro (d > 0.1 mm) and micro circulation (d < 0.1 mm), respectively. From the non-Newtonian fluid mechanics point of view [34] suggested an intermediate range called mesocirculation (50 μm < d < 300 μm).
Taking into account the geometries of the arterial-cephalic fistulae studied here, with dimensions greater than 1 mm, blood is being considered as a Newtonian fluid.
Consider a 3-D domain, 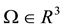 , with boundary
, with boundary , where i stands for inlet, o for outlet and w for wall, and time t:
, where i stands for inlet, o for outlet and w for wall, and time t: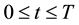 , with T being the pulse period. Then, Newtonian incompressible transient blood flow can be modeled by the following conservation of mass and momentum equations
, with T being the pulse period. Then, Newtonian incompressible transient blood flow can be modeled by the following conservation of mass and momentum equations
 (1)
(1)
![]()
Figure 1. Scheme for arteriovenous fistulae.
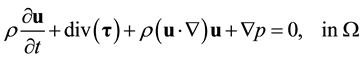 (2)
(2)
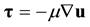 (3)
(3)
subject to the boundary conditions
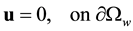 (4)
(4)
 (5)
(5)
 (6)
(6)
where 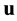 is the velocity vector,
is the velocity vector,  is the hydrostatic pressure,
is the hydrostatic pressure, 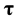 is the deviatoric part of the stress tensor,
is the deviatoric part of the stress tensor, 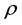 is the blood density (here set as 1045 kg/m3),
is the blood density (here set as 1045 kg/m3), 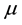 is the blood viscosity (considered 4.0 mPa.s), div is the divergence operator,
is the blood viscosity (considered 4.0 mPa.s), div is the divergence operator, 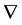 is the gradient operator and
is the gradient operator and ![]() is the unit outward normal vector. Equations (4) and (5) represent nonslip and developed flow boundary conditions, and Equation (6) accommodates a pulsating function at the inlet of the artery, with pulse period
is the unit outward normal vector. Equations (4) and (5) represent nonslip and developed flow boundary conditions, and Equation (6) accommodates a pulsating function at the inlet of the artery, with pulse period ![]() with data taken from [2] which have been fitted here by Equation (7) and illustrated in Figure 2. This inlet pulsating velocity was prescribed for each anastomotic angle case as being a plug profile, according to the boundary condition Equation (6), which means a zero injection angle relative to the longitudinal axis of the artery, at a sufficient distance from the fistula (half of the artery length) to ensure fully developed flow before approaching the fistula. The systolic peak and the minimum diastolic are located at 0.25 s and 0.99 s, respectively.
with data taken from [2] which have been fitted here by Equation (7) and illustrated in Figure 2. This inlet pulsating velocity was prescribed for each anastomotic angle case as being a plug profile, according to the boundary condition Equation (6), which means a zero injection angle relative to the longitudinal axis of the artery, at a sufficient distance from the fistula (half of the artery length) to ensure fully developed flow before approaching the fistula. The systolic peak and the minimum diastolic are located at 0.25 s and 0.99 s, respectively.
![]() (7)
(7)
Once determined the velocity field, ![]() , the pressure field,
, the pressure field, ![]() , and the stresses,
, and the stresses, ![]() , for each time step, local absolute values of the instantaneous shear vector,
, for each time step, local absolute values of the instantaneous shear vector, ![]() , containing the shear components of the shear stress tensor, is calculated along the walls, WSS (wall shear stress):
, containing the shear components of the shear stress tensor, is calculated along the walls, WSS (wall shear stress):
![]() (8)
(8)
This is an important variable indicating the friction level at the wall. However, to analyze the WSS at each instant of time is unfeasible and it does not directly supply a measure of the oscillations of the shear stress field for the pulse period. Then, it will be used here the idea, first introduced by [40] , of an oscillatory shear index, OSI, through the form proposed by [7] , which is determined for each point of the vessel walls:
![]()
Figure 2. Pulsating flow entrance used in the simulations.
![]() (9)
(9)
Equation (9) quantify the degree of deviation of WSS from its medium direction during the whole cardiac period, ![]() , generated by reversions or secondary flow that occur due to the pulse [20] [41] .
, generated by reversions or secondary flow that occur due to the pulse [20] [41] .
2.3. Computational Model
To solve the equation system of the flow (Section 2.2) in the arteriovenuos geometric models for the six angles, a finite volume method, [42] , was used through the OpenFoam free platform [43] , adopting the well known PISO algorithm (Pressure Implicit with Splitting of Operators), [44] which is a modification of the classical SIMPLE (Semi-Implicit Method for Pressure Linked Equations) scheme [42] , by introducing an additional pres- sure correction step. This makes PISO to converge faster than SIMPLE and to better accommodate irregular cells. The process starts by solving the discretized pressure equation [45] by using the GAMG solver (Geometric Agglomerated Algebraic Multigrid Solver) from which a fast solution is obtained to generate a starting solution for the final finer mesh. For the solution of dicretized velocity equation [45] , the PBiCG solver was used. This is a preconditioner bi-conjugate gradient solver to asymmetric matrices. Additionally, a simple incomplete LU diagonal-based preconditioner, adequate to linear multigrid methods, was used [43] . In the computational experiments the meshes varied from 9000 for the 20˚ to 13,000 for the 45˚ angle hexahedral cells with time step of 10−5 s in all cases. Figure 3 depicts the final mesh for the 45˚ angle case, and illustrates the general aspect for the other angles. To change the anastomotic angles, but allowing sufficient hydraulic lengths to fully developed flow at the inlet and at the outlets, for all the angle cases the fistulae were placed at the mean length point of the artery. This is the rotation point for the half size of the vein, starting from the alignment of both longitudinal axes until reached the desired anastomotic angle (measured clockwise), with the remaining part maintained pa- rallel to the artery direction.
3. Computational Results and Discussions
Simulations have been performed for side-to-end radial-cephalic arteriovenous fistulae with pulsating antegrade flow, testing six anastomotic angles: 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚. Results are presented for velocity contour fill, stream lines, WSS for the peak systole and the minimum diastole instants and OSI for the during time period![]() . Figures 4(a)-4(f) illustrate the velocity contours and stream lines for the systolic peak
. Figures 4(a)-4(f) illustrate the velocity contours and stream lines for the systolic peak ![]() at the longitudinal section. It is observed that for higher angles, from 35˚ to 45˚, dense and large extents of stagnation regions are formed near the heels of the fistulae. This effect is smoothed when the angle decreases and is smaller for the 25˚ angle, even having some secondary flows as the others. Analogous patterns can be seen in the minimum diastolic
at the longitudinal section. It is observed that for higher angles, from 35˚ to 45˚, dense and large extents of stagnation regions are formed near the heels of the fistulae. This effect is smoothed when the angle decreases and is smaller for the 25˚ angle, even having some secondary flows as the others. Analogous patterns can be seen in the minimum diastolic ![]() results depicted in Figures 5(a)-5(f). Low/medium velocities appear in the 30˚ angle at the artery floor, down the section of the junction, and it is more pronounced for the angle of 20˚.
results depicted in Figures 5(a)-5(f). Low/medium velocities appear in the 30˚ angle at the artery floor, down the section of the junction, and it is more pronounced for the angle of 20˚.
Figures 6(a)-6(f) present the results for WSS in the systolic peak. They are very non-homogenous, with the higher values occurring along the proximal artery branches and smaller ones at the veins. Long extents of higher values than the normal ones (2.0 - 7.0 Pa) are present in this peak for all configurations, but the angles of 35˚ to
![]()
Figure 3. Arteriovenous fistula 3D model―general mesh used.
45˚ present these values even at the ceiling of the distal artery branch. The most homogeneous distribution of WSS is presented by the angle of 25˚, considering the normal range (light blue to orange colors in the graphic scale). The same can be observed when looking the minimum diastolic results of Figures 7(a)-7(f). But in these critical cases, at the regions of the junctions, the most favorable (higher values of WSS in longer extents and bounded by the normal values) are the angles of 25˚, 20˚, and 30˚, in this order. Angles of 35˚ to 45˚ present unfavorable very low WSS values along the veins and at the junction.
Systolic peak and minimum diastolic are only two instants of the whole pulse period. Although that wall shear stress levels are very important to cause intimal pathologies, their variations and oscillations are reported as being of major importance for stenosis formation, especially at the junction region. Then, results for the oscillation shear index have been obtained here by Equation (9), previously defined, which takes into account a mean variation of the shear stress along the whole period at each point of the walls. Figures 8(a)-8(f) illustrate these results at the junctions. Dark blue color contours indicate very low or null oscillation levels, OSI < 0.01, while OSI > 0.01 indicate higher oscillation degrees. Two views for each angle case are presented to better locate the regions with higher OSI. It can be observed that the areas with higher oscillations are placed near the junctions, with the angles of 35˚ to 45˚ presenting greater extents of high OSI. The angle of 25˚ presented smaller areas of high OSI followed by the angles of 20˚ and 30˚.
4. Conclusions
In this work, 3-D arteriovenous radial-cephalic side-to-end fistulae with antegrade blood flow have been computationally modelled for anastomotic angles of 20˚, 25˚, 30˚, 35˚, 40˚ and 45˚, to investigate anatomical configurations that could generate more favorable hemodynamic conditions, to minimize the problems related with fistulae failures. Large vessel blood flow model has been considered and a Finite Volume computational method was used to solve the equations for the pulsating flow problems in the OpenFoam free software platform. To analyze the possibility of stenosis formation, results were obtained here for wall shear stress, oscillatory index, velocity contour fill and local circulation fields. From the results, it is possible to conclude:
・ From the velocity fields and, especially, from the stream lines, higher angles presented more secondary flows and larger extensions of stagnation regions near the critical areas of the junctions;
・ From the WSS results, higher stresses have been detected along the artery walls than along the veins, and smaller angles being more favorable since they presented higher shear stress levels along the areas close to the junctions as well as a more homogeneous distribution;
・ From the OSI, it was possible to better analyze the effects of oscillating shear at the walls, from which the higher it is, the higher is the possibility of pathologies to come up. The 25˚ angle presented less extension areas of high OSI, followed by 20˚ and 30˚;
・ As a consequence it is suggested here that the range 25˚ ± 5˚ is the most favorable for clinical applications.
・ The results here predict larger areas of oscillation shear at the fistulae as in [30] , however, they spread out along the veins.
・ There is an evident correspondence between the sites of stagnation areas and those of higher OSI.
Acknowledgements
J. A. Silva acknowledges the financial support of CAPES, J. Karam-Filho acknowledges CNPq/FAPERJ and C. C. H. Borges is thankful to CNPq, FAPEMIG and CAPES.
NOTES
*Corresponding author.