Programming First Integral Method General Formula for the Solving Linear and Nonlinear Equations ()
1. Introduction
Partial differential equations arise frequently in the formulation of fundamental laws of nature and in the mathematical analysis of a wide variety of problems in applied mathematics, mathematical physics, and engineering science. This subject plays a central role in modern mathematical sciences, especially in physics, geometry, and analysis. Many problems of physical interest are described by partial differential equations with appropriate initial and/or boundary conditions. These problems are usually formulated as initial-value problems, boundary- value problems, or initial boundary-value problems, a broad coverage of the essential standard material on linear partial differential equations and their applications is required. The study of the solutions of partial differential equations (PDEs) has enjoyed an intense period of activity over the last forty years from both theoretical and numerical points of view. Many methods obtaining the exact solution of non linear equation, some of the techniques are the bilinear transformation [1] , the sine cosine method [2] , F-expansion method [3] , the first integral method was first proposed by Feng [4] to solving Burger-Korteweg-devries equation and so on, in this paper investigation a traveling wave solution for non linear partial differential equation, study nonlinear phenomena, in solving modified KdV-kp can be based on the theory of commutative algebra, using the first integral method technique to solving linear and nonlinear equations.
2. First Integral Method
The non-linear partial differential equation form:
 (1)
(1)
where  is the solution of (1) we use the transforms:
is the solution of (1) we use the transforms:
 (2)
(2)
we use the wave transforms :
 (3)
(3)
Equation (1) transforms the ordinary differential equations we obtain:
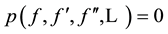 (4)
(4)
Anew independent variable:
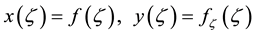 (5)
(5)
The system of ordinary differential equations:
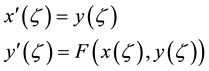 (6)
(6)
By the qualitative theory of differential equation [5] , we find the integral of (6) under same condition, then the general solution of (6) can be obtained directly. However, in general, it is really difficult for us to realize this even for one first integral, because for a given plane autonomous system, find its first integral will apply the Division theory to option first integral (6), An exact solution of (1) obtained by solving this equation. Now let us recall the Division theory.
Division theorem:
Suppose that  and
and 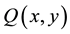 are polynomials of two variables
are polynomials of two variables 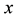 and
and  in
in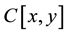 . And
. And 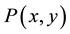 is irreducible in
is irreducible in . If
. If 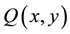 vanishes at all points of
vanishes at all points of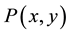 , then there exists a polynomial
, then there exists a polynomial ![]() in
in ![]() such that
such that![]() .
.
3. The First Integral Method General Formula
We discuss the problem by using the first integral method, consider the general formula:
![]() (7)
(7)
where ![]() are real constant. Using (7) in (6) we get the system.
are real constant. Using (7) in (6) we get the system.
![]() (8)
(8)
Now Appling Division theorem, suppose that ![]() and
and ![]() are nontrivial solution of (8):
are nontrivial solution of (8):
![]() (9)
(9)
Is an irreducible polynomial in the complex domain ![]() such that:
such that:
![]() (10)
(10)
![]() are polynomial and
are polynomial and![]() , Equation (16) called first integral method, there exist a polynomial
, Equation (16) called first integral method, there exist a polynomial ![]() in the complex domain
in the complex domain ![]() such that:
such that:
![]() (11)
(11)
which can be written as:
![]() (12)
(12)
by comparing with the coefficient of ![]() on both sides of (12), we get:
on both sides of (12), we get:
![]() (13a)
(13a)
![]() (13b)
(13b)
![]() (13x)
(13x)
![]() (13y)
(13y)
from (12a), we deduce that ![]() is a constant and
is a constant and![]() , we take
, we take![]() , and balancing the degrees of
, and balancing the degrees of![]() , we find the deg g(X).
, we find the deg g(X).
Now we take these cases:
Case 1:
Suppose that M = 1, in (12), then the (13) becomes:
![]() (14a)
(14a)
![]() (14b)
(14b)
![]() (14c)
(14c)
since ![]() are polynomial, then from (14a) we deduce that
are polynomial, then from (14a) we deduce that ![]() is constant and
is constant and ![]() for simplicity, take
for simplicity, take![]() . Balancing the degrees of
. Balancing the degrees of ![]() and
and![]() . We conclude that
. We conclude that![]() , suppose that
, suppose that![]() , then we find
, then we find![]() .
.
![]() (15)
(15)
where ![]() is arbitrary integration constant. Substituting
is arbitrary integration constant. Substituting ![]() in (14c), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
in (14c), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
![]() (16)
(16)
using (16) in (10), we obtain:
![]() (17)
(17)
combining (17) with (8), and fine the exact solution (8).
Case 2:
Suppose that M = 2, in (12), then the (13) became:
![]() (18a)
(18a)
![]() (18b)
(18b)
![]() (18c)
(18c)
![]() (18d)
(18d)
since ![]() are polynomial, then from (14a) we deduce that
are polynomial, then from (14a) we deduce that ![]() is constant and
is constant and ![]() for simplicity, take
for simplicity, take![]() . Balancing the degrees of
. Balancing the degrees of ![]() and
and![]() . We conclude that
. We conclude that![]() , suppose that
, suppose that![]() , then we find
, then we find![]() :
:
![]() (19)
(19)
![]() (20)
(20)
where ![]() are arbitrary integration constants. Substituting
are arbitrary integration constants. Substituting ![]() in (18d), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
in (18d), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
![]() (21)
(21)
using (20) in (9),we obtain two equal roots for Y:
note that:
![]() (22)
(22)
combining (21) with (8), and fine the exact solution (8).
Case 3:
Suppose that M = 3, in (12), then the (13) became:
![]() (23a)
(23a)
![]() (23b)
(23b)
![]() (23c)
(23c)
![]() (23d)
(23d)
![]() (23e)
(23e)
since ![]() are polynomial, then from (14a) we deduce that
are polynomial, then from (14a) we deduce that ![]() is constant and
is constant and ![]() for simplicity, take
for simplicity, take![]() . Balancing the degrees of
. Balancing the degrees of ![]() and
and![]() . We conclude that
. We conclude that![]() , suppose that
, suppose that![]() , then we find
, then we find![]() :
:
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
where ![]() are arbitrary integration constants.
are arbitrary integration constants.
Substituting ![]() in (18d), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
in (18d), and setting all the coefficients of powers X to be zero, we obtain a system of nonlinear algebraic equations and by solving it, we obtain:
![]() (27)
(27)
using (20) in (9), we obtain three equal roots for Y:
note that:
![]()
then
![]() (28)
(28)
combining (21) with (8), and fine the exact solution (8).
Case n:
Suppose M = n, we get:
![]() (29)
(29)
Theorem 3.1:
The exact solution of the general formula in (7) are given by combining of (17), (21), (27) … (29), with (8) and integration respect with![]() .
.
4. Application
We can apply Theorem 3.1 to studying some nonlinear differential equations, as solitary wave equation.
Example 4.1:
The linear ODES:
![]() (30)
(30)
which is the same form of Equation (7), where:
![]()
![]() (31)
(31)
![]() (32)
(32)
integration respect to![]() :
:
![]() (33)
(33)
![]() (34)
(34)
so the (31) + (32) is the solution:
![]()
Example 4.2:
Consider the Boussines equation given by:
![]() (35)
(35)
using ![]() into (34) gives:
into (34) gives:
![]() (36)
(36)
where integrating twice yields:
![]() (37)
(37)
which is the same form of (7), where:
![]()
![]() (38)
(38)
![]() (39)
(39)
integration respect to ![]() then:
then:
![]() (40)
(40)
Example 4.3:
Consider the Gardner equation given by:
![]() (41)
(41)
using the wave variable ![]() and integrating the result will convert the (41) to the ODE:
and integrating the result will convert the (41) to the ODE:
![]() (42)
(42)
which is the same form of (7) where:
![]()
![]() and (43)
and (43)
so:![]() (44)
(44)
integrating respect to ![]() then:
then:
![]() (45)
(45)
Example 4.4:
Consider the nonlinear Schrödinger equation:
![]() (46)
(46)
suppose that (46) has solution form:
![]() (47)
(47)
substituting (47) in (46), then (46) become:
![]() (48)
(48)
which is the same form of (48), where:
![]()
![]() (49)
(49)
![]() (50)
(50)
integrating respect to ![]() then:
then:
![]() (51)
(51)
Example 4.5:
The Cahn-Allen equation: we study nonlinear parabolic PDF given by:
![]() (52)
(52)
using the wave variable ![]() and integrating the result will convert the (52) to the ODE:
and integrating the result will convert the (52) to the ODE:
![]() (53)
(53)
which is the same form of (48), where:
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
integrating respect to ![]() then:
then:
![]() (57)
(57)
![]() (58)
(58)
![]() (59)
(59)
![]() (60)
(60)
our result can be compared to Wawaz’s result [2] .
5. Conclusion
The first integral method a general formula, is successful for solving a lot of nonlinear equation, and establishing travelling wave solutions, which is based on the ring theory of commutative algebra, and used to solve complicated and tedious algebra calculation. We can also apply them to some other nonlinear partial differential equations.