1. Introduction
Today, one of the well-known facts of space dynamics is the desperate needs of the universal formulations of orbital motion. This is because, in complete interplanetary transfer, all types of the two body motion (elliptic, parabolic, or hyperbolic) appear, moreover, the given type of an orbit is occasionally changed by perturbing forces acting during finite interval of time. Thus far, we have been obliged to use different functional representations for motion depending upon the energy state (elliptic, parabolic, or hyperbolic) and a simulation code must then contain branching to handle a switch from one state to another. In cases where this switching is not smooth, branching can occur many times during a single integration time-step causing some numerical “chatter”. Consequently, through the use of the universal formulations, orbit predictions will be free of the troubles, since a single functional representation suffices to describe all possible states.
Recently Sharaf and Saad [1] (hereafter will be referred to as Paper I) established new set of the universal functions (Y-functions) for the two-body initial value problem. Due to the importance of accurate universal orbital predications using the Y-functions, an efficient algorithm based on the continued fractions theory was established for these functions.
2. The Universal Y’s Functions
The universal Y’s functions are given by:
 (1)
(1)
where  is to be considered, as a new independent variable―a kind of generalized anomaly,
is to be considered, as a new independent variable―a kind of generalized anomaly, 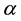 is just the inverse of the semi-major axis a given as:
is just the inverse of the semi-major axis a given as:
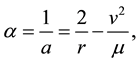 (2.1)
(2.1)
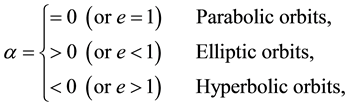 (2.2)
(2.2)
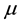 is the gravitational parameter, finally, r and v are the magnitudes of the position and velocity vectors respectively.
is the gravitational parameter, finally, r and v are the magnitudes of the position and velocity vectors respectively.
What concerns us among the properties of the Y’s functions given in Paper I are:
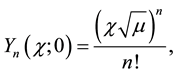 (3.1)
(3.1)
 (3.2)
(3.2)
Figure 1 and Figure 2 show the three dimension visualizations of  with
with  and
and .
.
3. Continued Fraction Method
In fact, continued fraction expansions are generally far more efficient tools for evaluating the classical functions
![]()
Figure 1. Visualization of Y1 function in three-dimensional space.
![]()
Figure 2. Visualization of Y2 function in three-dimensional space.
than the more familiar infinite power series. Their convergence is typically faster and more extensive than the series.
Top-Down Continued Fraction Evaluation
There are several methods available for the evaluation of continued fraction. Traditionally, either the fraction was computed from the bottom up, or the numerator and denominator of the nth convergent were accumulated separately with three-term recurrence formulae. The drawback of the first method is obviously, having to decide far down the fraction to being in order to ensure convergence. The drawback to the second method is that the numerator and denominator rapidly overflow numerically even though their ratio tends to a well-defined limit. Thus, it is clear that an algorithm that works from top down while avoiding numerical difficulties would be ideal from a programming standpoint.
Gautschi [2] proposed very concise algorithm to evaluate continued fraction from the top down and may be summarized as follows. If the continued fraction is written as
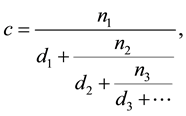
then initialize the following parameters
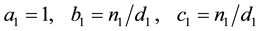
and iterate 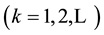 according to:
according to:
![]()
In the limit, the c sequence converges to the value of the continued fraction. Continued fraction method was used in many problems in astrophysics [3] [4] as well as in special functions of astrodynamics [5] [6] .
4. Evaluation of the Y’s Functions
In the following, we shall consider the evaluations of the four functions ![]() only, because these four functions appear in the orbital motion when treated by the Y’s functions (see Paper I) , on the other hand, the functions
only, because these four functions appear in the orbital motion when treated by the Y’s functions (see Paper I) , on the other hand, the functions ![]() could be obtained from
could be obtained from![]() by using the recurrence relation (3.2) for
by using the recurrence relation (3.2) for ![]() and directly from Equation (3.1) if
and directly from Equation (3.1) if ![]()
4.1. Expression of ![]() as Continued Fractions
as Continued Fractions
From the expressions of tanx and ![]() as continued fractions [7] for any
as continued fractions [7] for any ![]() we can show that,
we can show that,
![]()
where
![]()
4.2. Computational Algorithm
Input: ![]()
Output ![]()
Computational sequence
1-Compute a’s from
![]()
2-Compute u from the continued fraction
![]()
by using Gautschi’s algorithm of Subsection 3.1
3-![]()
4-![]()
5-![]()
6-![]()
7-![]()
8-The algorithm is completed.
4.3. Numerical Applications
The applications of the above algorithm for the numerical values of![]() ,
, ![]() and for some values of
and for some values of![]() , are listed in Table 1.
, are listed in Table 1.
![]()
Table 1. Numerical values of Y0,1,2,3, μ = 1 for some values of α and χ.
The more accurate calculation of![]() , the more accurate orbit determination. That is because the universal Kepler’s equation is expressed in terms of Y’s functions [1] . Thus efficient tools used for evaluating Y’s functions have contributions in well describing the two-body initial value problem.
, the more accurate orbit determination. That is because the universal Kepler’s equation is expressed in terms of Y’s functions [1] . Thus efficient tools used for evaluating Y’s functions have contributions in well describing the two-body initial value problem.
5. Conclusion
In concluding the present paper, an efficient algorithm based on the continued fractions theory was established for the recent universal Y’s functions of space dynamics. The algorithm is valid for any conic motion (elliptic, parabolic or hyperbolic).