Assessment of Urban Heat Island Using Remotely Sensed Imagery over Greater Cairo, Egypt ()
1. Introduction
Urban development has some negative impacts on the global environmental quality, including air quality, temperature increases and landscape alteration. It also leads to conversion of agricultural land and loss of biodiversity (Santamouris et al., 2001) [1] . Urban heat island (UHI) is a climatic phenomenon where urban areas have higher air temperature than their rural surroundings due to the anthropogenic modifications of land surfaces. There are two types of urban heat islands, surface and atmospheric UHI. A combination of factors leads to the development of the UHI. UHI is measured by surface temperature, which can vary between the city and rural area by up to 5˚C (United Nations, 2010) [2] .
Many Factors contribute to UHI, such as: building material thermal properties, urban design geometry (urban canyon), anthropogenic factors and altered land cover. Building material reflectance is generally low so they reflect less and absorb more energy which leads to increasing temperatures at surface level. Building materials have high remittance values so they release heat quickly and stay cooler. Common building materials such as tar, asphalt, brick and concrete store solar energy during the day and release it at night, so UHI intensity is reported to be stronger at nighttime. Urban design geometry is one of the UHI leading factors where urban canyons are created by narrow streets and tall buildings. These decrease wind speeds and increase reflective surfaces that trap heat. Anthropogenic factors such as waste heat from vehicles and buildings; altered land surface cover so porous vegetation is replaced with non-porous materials thus restricting evaporative cooling [3] [4] .
Attempts to extract the land surface temperature (LST) from remote sensing data have been undertaken for several decades [5] - [18] . Remote sensing data supply a practicable approach for the investigation of LST on wide spatial and temporal scales. Satellite thermal infrared (TIR) sensors measure top of the atmosphere (TOA) radiances, from which brightness temperatures can be derived based on Plank’s law [15] . The TOA radiance is the mixing result of three fractions of energy, earth’s surface emitted radiance, atmosphere upwelling radiance, and sky down welling radiance. Top of atmosphere and land surface brightness temperature differences generally range from 1 Kelvin to 5 Kelvin in the 10 - 12 μm spectral regions, and such differences depend on the atmospheric conditions [19] . Therefore, atmospheric effects, including absorption, upward emission, and downward irradiance reflected from the surface, have to be corrected before land surface brightness temperature obtained [20] . These brightness temperature should be further corrected with ground emissivity values prior to the computation of LST to account for the roughness properties of the land surface, the amount and nature of vegetation cover, and the thermal properties and moisture content of the soil [21] . Methods to retrieve LST are depending on how the sensor’s thermal bands were designed. one can classify satellites according to the number of thermal bands to a) single thermal band such as Landsat satellites, b) two thermal bands such as NOAA, AVHRR, ATSR (Along-track scanning radiometer) and GOES (Geostationary operational environmental satellite) satellites, c) multiple thermal channels such as ASTER and MODIS satellites. The split-window algorithms have been widely used for estimating LST from two thermal bands in the 10.5 - 12.5 µm region with given surface emissivity. Many split-window formulas are published in the literature such as those implemented by [5] [8] [10] [22] [23] . For multiple thermal band satellites, some other formulae were developed to retrieve more accurate LST and emissivity from the satellite image itself. Among these formulas are: the day/night algorithm which is used for MODIS [16] , the reference channel method [24] [25] Alpha-derived emissivity (ADE) method [6] [9] [26] which is known as alpha-residual technique, Temperature-Independent Spectral Indices (TISIs) [22] [27] Optimization Algorithm [13] [28] [29] and the ASTER Algorithm [12] [28] [29] . There are three basic modules in the ASTER algorithm 1) normalized emissivity method, 2) ratio module and 3) maximum-minimum difference module. The main difference between the three modules is the way to estimate the ground emissivity from the ASTER image. Numerical simulations show that ASTER algorithm can estimate LST to within error of 1.5 K and emissivity to within 0.015 [30] . However, as [15] reported that algorithm requires an accurate atmospheric correction. Running ASTER algorithm on airborne multispectral thermal data applied this algorithm to TIMS (Thermal Infrared Multispectral Scanner) resulted in LST with typical errors of 3 K [11] . However, for satellites with a single thermal band, such as Landsat TM and ETM+, obtaining LST is more difficult. In addition to an accurate radiative transfer model and some knowledge of the atmospheric profile, emissivity information is also required [14] . The most common methods adapted for retrieving LST from the Landsat TM and ETM+ thermal data are: 1) the radiative transfer equation, 2) mono-window algorithm, and 3) Jiménez-Muñoz and Soprano’s algorithm [17] . The first method requires in situ measurements of atmospheric data simultaneously with the satellite pass which in turn may be constrain for using that method. Meanwhile, the second
and the third one could be used in the absence of these data. The second and the third methods use NDVI for calculating ground emissivity.
Landsat thermal infrared (TIR) channel, band 6 records the radiation with spectral range in 10.4 - 12.5 μm from the surface of the earth. Different LST retrieval methods have been developed according to different data sources, such as the split-window method, temperature/emissivity separation method [5] [10] [17] , mono- window method [14] , and the single-channel method. Among of these methods three LST retrieval methods: radiative transfer equation, mono-window algorithm and single-channel algorithm can be applied to Landsat data. Although all of these methods can provide good results, the radiative transfer equation is not available without in situ parameters of atmospheric profiles simultaneously measured when the satellite passes over. In addition, mono-window algorithm can produce better results than the single-channel algorithm with a root mean square deviation of 0.9 [17] . Thus, the mono-window algorithm is applied in this study to retrieve the LST of the investigated study areas from Landsat. [14] proposed the mono-window algorithm for retrieving LST from Landsat data. Based on thermal radiance transfer equation, the mono-window algorithm only requires three parameters emissivity, transmittance and effective mean atmospheric temperature to retrieve LST from Landsat.
[31] reported very few UHI studies conducted in the African continent so there is a need for such studies in order to inform city planners to cope with the challenges of urban climates. The main objective of this study is to use Landsat data to investigate the UHI effect on three Egyptian cities. These cities are located within the Greater Cairo, and include Cairo, Giza and Qalubiya.
2. Material and Methods
2.1. Study Area
Greater Cairo includes Cairo, Giza and Qalubiya governorates (Figure 1). Greater Cairo is the largest metropolitan area in Egypt and the largest urban area in Africa.
The region is situated between 29˚43'N and 30˚26'N latitudes and the 30.717˚E and 31.883˚E longitudes with an area of 1.09 million acres. The topography of the region is almost flat, bounded by hills to the east and west. It is located in the subtropical climatic region with a dry climate. In winter (December to February), the general climate of the region is cold, moist and rainy with minimum mean temperature of 13˚C, while during summer (June to August), it is hot and dry with maximum mean temperature of 28˚C. In spring (March to May) and autumn (September to November) dust and sandstorms frequently blow [32] . The total population of the study area is approximately 20 million as illustrated in Table 1.
2.2. Data Used
Two types of data were collected for this study: remotely sensed data in the form of four Landsat ETM+ (Table 2) and meteorological data from the nearest station to the study area. The meteorological data were obtained from the Central Laboratory of Agriculture Climate (CLAC). The data include: minimum and maximum temperatures, relative humidity and wind speed and direction in hourly formats for the chosen dates of the study.
3. Data Analysis and Processing
3.1. Meteorological Data Analysis
The meteorological data were used to calculate water vapor content, atmospheric transmittance and mean atmospheric air temperature
3.1.1. Calculation of Water Vapor Content (Pw)
Relative humidity is defined as the ratio of the water vapor at a given temperature to the saturation water vapor pressure at the same temperature which can be expressed as the following Equation (1):
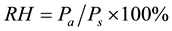 (1)
(1)
where RH is the relative humidity, Pa is the actual water vapor pressure and Ps is the saturation water vapor pressure. The above equation can be written as:
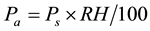 (2)
(2)
![]()
Figure 1. False color composite (4, 3, 2) Landsat 7 ETM+ image for the study area.
![]()
Table 1. Population estimates by governorate.
![]()
Table 2. Dates and statues for Landsat ETM+ downloaded images.
According to [33] Ps at a given Temperature (K) can be calculated from the following Equation (3):
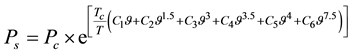 (3)
(3)
where:
T = ambient temperature in K.
Ps = Saturation vapor pressure (hPa).
Tc =Water Critical temperature, 647.096 K.
Pc = Critical pressure 220,640 hPa.
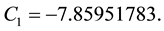
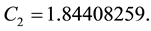
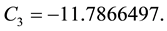
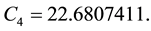
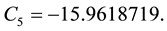
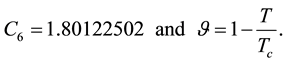
3.1.2. Calculation of Atmospheric Transmittance (t)
Atmospheric transmittance can be defined as the capacity of the atmosphere to transmit electromagnetic energy. Atmospheric transmittance is dependent on the air mass penetrated by rays, as well as on the amount of water vapor and dust in the air. It varies for radiations of different wavelengths; the smaller the atmospheric absorption and scattering of light, the greater the atmospheric transmittance.
According to [14] , atmospheric transmittance could be calculated based on some linear equation estimated from statistical regression analysis. These equations correlate the atmospheric transmittance to the water vapor content (g/cm2) calculated from the above section. Table 3 gives the different atmospheric transmittance equations for different water vapor ranges:
3.1.3. Calculation of Atmospheric Mean Temperature (Ta)
From [14] , following Equations (4a) and (4b) can be used to estimate the atmospheric mean temperature based on given near surface air temperature:
For mid-latitude summer
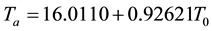 (4a)
(4a)
For mid-latitude winter
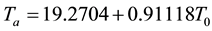 (4b)
(4b)
3.2. Satellite Data Analysis
The striped satellite images were filled using the Landsat gap filling module embedded in ENVI using another image very close in date of acquisition from the original one, after getting a clear complete scene the following steps were done.
3.2.1. Conversion of the Digital Number (DN) to Spectral Radiance
In order to convert the DN data from Landsat to spectral radiance, Equation (5) can be written as:
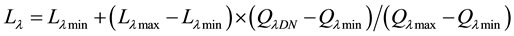 (5)
(5)
where Lλ is the at-sensor spectral radiance (watts/(meter squared × ster × μm)); Lλmax is the maximum at-sensor spectral radiance; Lλmin is the minimum at-sensor spectral radiance; 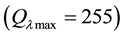 and
and ![]() represents
represents
![]()
Table 3. Transmittance calculation equations.
the maximum and minimum DN value of pixels and QλDN represents the DN value of pixel [34] .
For Landsat ETM+ data, Equation (5) can be expressed as follow:
1) For low gain band
![]() (6a)
(6a)
2) For high gain band
![]() (6b)
(6b)
3.2.2. Conversion of Spectral Radiance to at-Sensor Temperature (Ti)
ETM+ Band 6 imagery can also be converted from spectral radiance (as described above) to at-satellite temperatures of the viewed Earth-atmosphere system under an assumption of unity emissivity and using pre-launch calibration constants. The conversion formula is:
![]() (7)
(7)
where ![]() is the at sensor temperature in Kelvin, K1 and K2 are pre-launch calibration constants and Lλ is the spectral radiance in watts/(meter squared × ster × μm). For Landsat 7 ETM+ the calibration constants are K1 = 666.09 (watts/(meter squared × ster × μm)), K2 = 1282.71 Kelvin (Landsat 7, 1998)
is the at sensor temperature in Kelvin, K1 and K2 are pre-launch calibration constants and Lλ is the spectral radiance in watts/(meter squared × ster × μm). For Landsat 7 ETM+ the calibration constants are K1 = 666.09 (watts/(meter squared × ster × μm)), K2 = 1282.71 Kelvin (Landsat 7, 1998)
3.2.3. Emissivity Estimation (Ɛi)
The emissivity can be calculated from NDVI. According to [18] , land surface emissivity can be calculated from NDVI as follow (Table 4).
3.2.4. Retrieval of LST
The mono-window algorithm [14] can be written as Equations (8)-(10). Three variables (i.e., emissivity, transmittance and effective mean atmospheric temperature) are required as below:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where: Ts is the LST in Kelvin, Ti is the at-sensor temperature (K), ![]() is the emissivity estimated from NDVI, t is the atmospheric transmittance calculated from water vapor content, Ta is the mean atmospheric temperature, a = −67.355351, and b = 0.458606.
is the emissivity estimated from NDVI, t is the atmospheric transmittance calculated from water vapor content, Ta is the mean atmospheric temperature, a = −67.355351, and b = 0.458606.
All of these calculations were put together in a model using ERDAS IMAGIN software to automate the pro- cess, as illustrated in the figure below (Figure 2).
4. Sensitivity Analyses for the LST Retrieving Algorithm
Sensitivity analysis is used to test how much is a model sensitive to changes in the value of its parameters;
![]()
Table 4. Emissivity estimations equations.
which is usually performed as a series of tests using different sets of parameter values to see how a change in the parameter causes a change in the behavior of a model.
The mono-window algorithm relies on three parameters to estimate LST: ground emissivity, atmospheric transmittance and effective mean atmospheric temperature. Due to all of these parameters are empirically calculated by mathematical equation not measured in situ so sensitivity analysis is required to understand the behavior of these parameters and to judge the model accuracy and limitations.
The following Equation (11) used for estimation the estimated error due change of each one of these parameters at once:
![]() (11)
(11)
where ![]() s is LST estimation error, x is the variable to which the sensitivity analysis ongoing,
s is LST estimation error, x is the variable to which the sensitivity analysis ongoing, ![]() is possible error of the variable x,
is possible error of the variable x, ![]() and
and ![]() are the LST simulated by the given algorithm for
are the LST simulated by the given algorithm for ![]() and x respectively.
and x respectively.
The overpass of Landsat ETM+ satellite on the study area is almost at 9:00Am, so the atmospheric air temperature is likely 20˚C. Near surface temperature is 30˚C in summer while in winter at the same time atmospheric air temperature is likely 10˚C, near surface temperature is 15˚C, this according to the obtained meteorological data. Emissivity is 95%, this because the study area is a huge urban area and asphalt and concrete are the most dominant land cover in the study area, meanwhile the sky condition is not the ideal case due to much more smog and dust so atmospheric transmittance accounted by 75%.
5. Results and Discussion
5.1. Sensitivity Analysis for the LST Retrieval Algorithm
Figure 3(a) shows the LST error in corresponding to transmittance error at different transmittance levels i.e.
![]()
Figure 3. Probable LST estimation error due to the possible transmittance and emissivity error. (a) Average LST error against transmittance error, (b) (d) LST error against brightness temperature, and (c) Average LST error against emissivity error.
(50%, 60%, 70%, 80% & 90%). Data reveal that at high transmittance levels (90%) LST error is about 0.2˚C meanwhile as transmittance decreases LST estimation Error increase till 50% transmittance it reaches 2˚C. When testing the proper LST estimation error against different brightness temperature for different transmittance values as indicated in Figure 3(b), it reflects that; as brightness temperature increase from 0˚C to 20˚C the LST error decreases but after 20˚C it becomes a linear relationship with different slope, which depends on the transmittance value. It is clear that for small transmittance error (0.005%) the LST error is less than 1˚C on contrast to high transmittance error (0.06) it reaches 3˚C.
The model sensitivity to errors due to emissivity estimation errors is presented in Figure 3(c) and Figure 3(d). Figure 3(c) shows that LST estimation error is in linear relationship with the emissivity values i.e. (emissivity = 90%, 92%, 94%, 96% & 98%) for high emissivity values (>98%) the expected LST error is 1.2˚C when the emissivity error is 0.025% meanwhile as emissivity decrease to 90% the estimated error would be 1.4˚C. Figure 3(d) illustrates the linear relationship between the LST calculation error and the brightness temperature for different emissivity errors. It obviously shows that as emissivity error increases LST error increases rapidly.
5.2. LST Results
This study results emphasis that LST varies depending on the existing land use/ land cover. In general, UHI exists on some urban centers across the investigated cities. The value of the UHI in some centers ranged between 0.5˚C to 2˚C in winter and 1˚C to 3˚C in summer above the mean of the peripheries.
UHI over Greater Cairo
Spatial distribution of LST over the Greater Cairo is shown in Figure 4, which explores the four different dates considered in the study. The summer season in the top (a, b) of the figure with year 2002 on the left and 2012 on the right while winter season on the bottom (c, d) of the figure and also 2002 on the left and 2012 on the right.
For the summer season, the LST ranged between 27˚C to 61˚C. The lowest temperature was recorded from the surface water bodies, while the highest LST comes from the fine sand in the eastern and western deserts. The vegetated areas record an average temperature of 35˚C. The urban areas surface temperatures ranges between 40.56˚C to 57.57˚C in summer seasons and 19.58˚C to 26.57˚C in winter seasons (Table 5).
![]()
Figure 4. LST distribution on the greater Cairo for the 2002 & 2012 (summer and winter).
![]()
Table 5. Mean, Min & Max LST over Greater Cairo urban areas.
One of the most important factors leading the UHI phenomena is the land cover land use. Figure 5 shows the LST profile for a small area with bare soil in the study area which has a clear increase in the surface temperature from the surrounding cover which is defined as surface heat islands. Although this area is very small (280 acre) and is surrounded by vegetation, it has a relatively high temperature (10˚C) difference from the surrounding cover.
It is clear that temperature difference increases towards to the center of the urban area and decrease in the direction of the peripheries and this is defined as urban heat islands.
Figure 6 represents values and the normalized ((Pixel value―the mean of the district)/the standard deviation) values of the LST over the center points of the study area districts (Markaz & kism). The urban heat island in the
![]()
Figure 5. Cross sectional profile for one of UHIs detect in the study area.
study area is defined as the urban areas that has normalized value greater than 2. From Figure 6, UHI ranged between 0.5˚C and 3.5˚C above the mean temperature of the districts peripheries.
Data shown in Figure 6 illustrate that there some districts have a UHI of value ranged between 0.8˚C to 3.5˚C, such as Qesm 15th of May, QesmAwal & Thani 6th of October and Qesm El-Sheikh Zayed which are big industrial areas in the Greater Cairo, meanwhile QesmMisr Al-Qadima which has UHI of value (0.85˚C - 2.7˚C) is characterized by the informal settlement and canyons (very narrow roads). Some new developed areas in the eastern side of the Greater Cairo such as El Shrook city and Qesm El-Obourhave normalized values ranged between (1.2˚C to 2.8˚C). This may be attributed to the dominant land cover which to a great extent is bare soil (fine sand and rocks).
6. Conclusions
In the absence and nonuniform distribution of ground weather stations, remotely sensed data have a great importance to monitor impacts of different environmental issues such as heat islands. The thermal band in Landsat satellite series i.e. (MSS, TM and ETM+) have been proven to have a crucial role in estimating surface temperature. Different algorithms developed by different authors to overcome the shortage of data required for calibrating the satellite estimated surface temperature relative to the field of study. The mono window algorithm developed by [14] is one of these algorithms that have a great importance in case of missing data of ground emissivity; atmospheric transmittance and mean atmospheric air temperature.
The obtained results from this study could be concluded in the following main points:
・ UHI exists regardless of the season i.e. winter or summer in the two investigated dates.
・ The two types of the heat islands, the surface and the urban one, exist in the study area.
・ The value of heat islands over the urban area is ranging between 0.5 and 3.5 degree above the mean temperatures of the urban areas and it is much related to the existing land use/land cover.
・ Urban Heat Island which is our main concern in this study is much related by the land use i.e. in the industrial areas it has a great effect such as what is recorded in Qesm 15th of May District (3.5 degree).
![]()
Figure 6. Normalized and mean value of the LST over Kism & Markaz of the Greater Cairo.
・ The impacts of UHI lead to more energy load for conditioning and with condition like what Egypt has from very poor planning in the old urban centers. The electricity cut off becomes a series problem and this may be an effect of the UHI phenomena.
・ Different factors contribute to the UHI such as roofs covering material, urban structure, existence of vegetation, street width, directions, etc.
Acknowledgements
The authors would like to thank the contribution of the Ministry of State for Scientific Research (Egypt) as well as the National Research Foundation (NRF) (South Africa) for their financial support of the project.
NOTES
*Corresponding author.