1. Introduction
Filter banks find application in various fields of signal, image and video processing for subband/transform coding [1] -[3] . In subband coding of images, filter banks are used to decompose the input image into several subimages in terms of different frequency bands. These subimages are then quantized and decoded to have compression with least distortion in reconstructed image quality. To get better resolution, decomposition in M bands can be achieved in one/two stage via M-channel filter bank or via repetitive use of wavelets (2 channel filter bank) in five/six stages [4] -[6] . Thus wavelet results in increased delay with nonuniform band decomposition. Filter banks are the most important component in image processing as the quality of the reconstructed image depends mainly on analysis/synthesis filter bank structure. Filter banks are designed as a transform to provide maximum energy compaction and decorrelation. To fulfil both the requirements, filter bank should have least stopband energy with least square error in overall transfer function. However, stopband attenuation increases if the perfect reconstruction condition is relaxed [7] . Amongst various types of transforms/filter banks cosine modulated, filter banks are the most popular choice as the designing and implementation both are easy as compared to others [8] [9] . Many approaches have been proposed for the design of 2 channel filter bank and M-channel CMFB filter banks with perfect and near perfect reconstruction condition since long time [10] - [11] . These approaches are based on the standard constrained, unconstrained, iterative least square optimization techniques which are in general complex, depend on the starting point and lead to local solution and may not fulfill all the objectives criterion. Further, quantization and coding of the transformed coefficients are achieved via progressive block based embedded image coder.
In this paper, an approach based on multiobjective optimization i.e. non-dominated sorting genetic algorithm [12] [13] is used to design M-channel uniform near perfect reconstruction Cosine modulated filter banks with coding gain given the highest priority amongst other objectives and Shapiro’s EZW coder with modifications suitable for block based transform coding is used for coding/decoding.
The organization of the paper is as follows: in Section 2, a relevant brief analysis of the pseudo cosine modulated filter bank is given. In Section 3 optimization problem is formulated. A brief overview of multiobjective optimization algorithm is explained in Section 4. In Section 5, design examples (cases) and results are presented with their application to image coding and conclusions are drawn in Section 6.
2. Problem Description
2.1. Design of Cosine Modulated Filter Bank
A typical M-band filter bank is shown in Figure 1. Input signal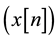 
is decomposed into M subband by analysis filters 
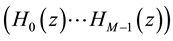in transmitter side, these subbands are then decimated by a factor of M. At the receiver side, these subband are up sampled and recombined to get the reconstruction output 
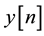with the aid of synthesis filters
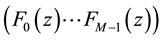. When these analysis /synthesis filters are cosine modulated version of a low pass prototype filter, then these filter banks are termed as cosine modulated filter banks. Based on input/output relationship of filter bank the reconstruction output is expressible as [14]
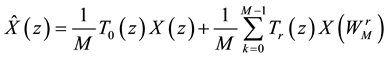(1)
where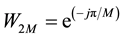
, M is no. of channels, 
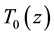is a distortion transfer function (determines overall amplitude distortion to input signal) and 
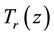is an aliasing distortion transfer function. In perfect reconstruction output signal is same as input except some delay i.e. 
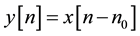for some integer
.
![]()
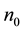Figure 1. M-channel maximally-decimated Filter bank.
In cosine modulated filter bank (CMFB) impulse response of all the analysis and synthesis filters generated from the prototype filter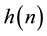 
via cosine modulation, can be expressed as follows
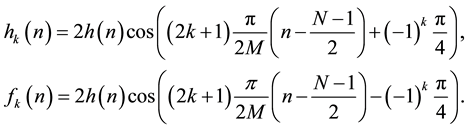(2)
For 
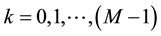and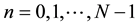
. The length N of 
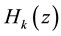and ![]()
are the same and multiple of 2M to satisfy linear phase property in prototype filters.
Design criteria for effective filter bank are:
2.1.1. NPR Condition
In M-band cosine modulated filter bank perfect reconstruction conditions [10] for the impulse response of the prototype filter ![]()
is
![]()
(3)
where![]()
, ![]()
, ![]()
and ![]()
is the integer part of n.
The near perfect reconstruction condition measure is expressed as
![]()
(4)
2.1.2. Coding Gain
A widely accepted measure of coding performance is the Coding Gain (CG) which measures the energy concentration capability of filter banks. By modeling a natural image as a one-dimensional Markovian source with a correlation factor ![]()
and by assuming uncorrelated quantization errors, Katto and Yasuda [15] derived a filter dependent coding gain given by:
![]()
(5)
where:![]()
, ![]()
and ![]()
and ![]()
are the ![]()
analysis and synthesis filter of the M-channel uniform filter bank ![]()
is the corresponding subsampling ratio, and ![]()
is the correlation factor.
2.1.3. Frequency Selectivity
As suggested in [7] , for high quality cosine modulated filter banks stop band mean energy of the prototype filter should be minimum and the magnitude distortion should be completely cancelled. Aliasing level in Pseudo CMFB can be kept small by keeping the attenuation large for![]()
. The stopband energy can be evaluated by the following expression
![]()
(6)
where ![]()
is the stopband edge of the prototype filter.
2.1.4. DC Leakage Free
In image coding, dc leakage free condition does not yield significant improvements in image quality [16] ; however, to minimize the checkerboard and ringing artifacts dc leakage in subbands other than the lowest one is desired. DC-leakage free property in the cosine modulated filter bank can be expressed as
![]()
(7)
3. A Multiobjective Genetic Algorithm for the Design of NPR Cosine Modulated Filter Bank
For optimizing a number of conflicting objective functions simultaneously, multiobjective optimization techniques are used. These techniques provide Pareto-optimal solutions instead of unique optimal solution. These solutions are optimal in the sense that no other solutions in the parameter space are superior to them when all the objective functions are considered [17] - [19] .
A multiobjective optimization can be stated mathematically as the minimization problem to minimize
![]()
(8)
where ![]()
and![]()
.
Vectors x and y represent the independent variables and the corresponding values of the individual objective functions respectively; on the other hand, X and Y are called the solution space and objective space, respectively.
The notion of Pareto-optimality is an important concept for multiobjective and explained in terms of a “dominance relation” as a solution ![]()
is said to dominate another solution ![]()
if the following conditions hold:
![]()
(9)
If a solution is not dominated by any other solutions among the entire objective functions than that solution is said to be a nondominated solution. The solutions that are nondominated regarding the entire parameter space are called Pareto-optimal solutions.
In our design, we search prototype filter h that minimize the three individual objective functions, namely, the energy of the filter stopband, near perfect reconstruction measure and the coding gain. To confine the search process in a feasible solution space, we impose dc leakage free condition as constraint. We have to determine only half of the coefficients since the remaining coefficients are obtained, by applying symmetry.
Our multi-objective optimization problem is formulated as follows:
![]()
(10)
Subject to the constraint: ![]()
In our case, a set of coefficients of the analysis filter bank ![]()
are treated as chromosomes which are optimized by the constrained multi-objective genetic algorithm (C-NSGA) to obtain a set of filter banks that minimize all the prescribed objective functions with a satisfactory level. This algorithm is based on the NSGA approach [12] .
4. Case Study
4.1. Filter Design Examples
Filter banks designed using non dominated sorting genetic algorithm here use some important parameters i.e. real valued filter coefficients for chromosome construction, crossover operator with distribution index of 20 and probability of 0.9, a polynomial mutation of distribution index 20 and probability of 0.01 are applied [12] [13] . The population size is set to 100 to find Pareto optimal solutions. Chromosomes of the initial population of filter
coefficients are set as ![]()
obtained by setting the starting vector as ![]()
else are equal to zero, satisfying the unit energy constraint between [−1, 1]. NPR condition is set by keeping the distortion to 10−5. The maximum generation ![]()
is set to 2000 generations. The programme was run using MATLAB 7.8 and the obtained coefficients were used for designing NPR cosine modulated filter bank. The amplitude response of the designed filter banks for 8 channel with 16 and 24 taps, with and without dc leakage condition are plotted in Figure 2 and Figure 3. The result of response indicates the superiority of the longer tap filters as the stopband attenuation increase with the increase in no. of taps. Secondly, incorporating dc leakage deteriorate the response of the filter but is good from the image coding point as dc leakage free condition reduce the aliasing errors and all the subband filters except the lowpass one, has at least one zero at ![]()
and thus all other bandpass and highpass filters are dc transmission free. Both the filter banks are designed giving highest priority to coding gain amongst the multiple objectives. The 8 × 16 CMFB in design Example I, with dc leakage (optimized for pure coding gain); attain 9.3749 dB, which almost equals the coding gain of optimal biorthogonal systems. However, applying dc leakage free constraints on the filter coefficients ensure a high level of perceptual performance in image coding. In design example II, the 8 × 24 case, our CMFB achieves an improvement of 0.001 dB in coding gain. CMFB’s with filter length 16 and 24 are shown in Figure 2 and Figure 3. Increasing the length only improves the coding gain marginally, it helps in the case of stopband attenuation (where longer filters are always beneficial), which result in more complexity in design and implementation.
![]()
(a)![]()
(b)
Figure 2. Magnitude Response of the NPR Cosine modulated filter bank with dc leakage free constraint for (a) 8 × 16; (b) 8 × 24.
![]()
(a)![]()
(b)
Figure 3. Magnitude response of the NPR pseudo QMF filter bank with DC leakage constraint designed using multiobjective optimization method for (a) 8 × 32; (b) 16 × 64.
Magnitude response of 8 Channel and 16 Channel NPR Pseudo QMF filter banks with 32 and 64 taps respectively, with dc leakage free constraint, designed using multiobjective optimization method, have been shown in Figure 3(a) and Figure 3(b) respectively. Although stopband attenuation is almost same for both the filter banks, clarity of magnitude response shows that the designed filter bank have least dc leakage with coding gain 8.8872 dB (8 × 32) and 9.03632 dB (16 × 64).
4.2. Application in Image Coding
The performance of our designed Cosine Modulated Filter Bank’s is evaluated through a progressive block based EZW image coder [20] merely replacing DCT by designed filter bank. In all simulations, we employed a 2 level decomposition of the 8-channel filter bank (1-D transform) separable implementation and symmetric extension at the edges. The coder is chosen to encode the transform coefficients because it provides some of the best performances of any image codec by using the zero tree approach for block based transform and generates an embedded coding which can be helpful in the reconstruction of images at different bitrates.
The images chosen for the coding experiments are Barbara and Boat. Both of them are standard, well known 512 × 512 8-bit gray-scale test images. The objective distortion measure is the popular peak signal-to-noise ratio (PSNR)
![]()
(11)
where, MSE denotes the mean squared error. Filter banks 8 × 16 and 8 × 24 were included in the tests, and both were optimized for maximum coding gain. Reconstructed images “Boat” and “Barbara” using designed filter bank (8 × 16) and (8 × 24) are shown in Figure 4(b), Figure 4(c) and Figure 5(b), Figure 5(c) respectively.
It is clear that longer filter banks with more no. of taps have the best characteristics with increase in PSNR. In this context, it is important to note that the filter length cannot be arbitrarily increased in order to increase PSNRs and achieve better frequency selectivity because long filters cause a ringing around edges artefacts when high frequency subband are coarsely quantized. Reconstructed images are better in visual quality as the frequency selectivity improves and overall distortion reduced, however, as the no. of taps increased artifacts become pronounced and PSNR decreases as the bit rates further reduced.
As shown in Figure 4 and Figure 5 for both the images performance of the designed CMFB is good as in low bit-rate coding image is reconstructed using only nonzero coefficients which are few in number and are very concentrated in lowest frequency component (lowpass filter output). Even though coding gain become lower, inclusion of dc leakage free condition leads to smooth reconstructed image as details are preserved.
Objective results for improvement in performance are shown in Table 1 and Table 2. In Table 1 designed filter bank with 24 taps is compared with baseline JPEG using (8 × 8 DCT) as transform and LOT and GENLOT [21] . It is clear that using multiobjective optimization the designed filter bank outperforms as both the coding gain and stopband attenuation are higher as compared other existing filter bank with same no. of parameters.
Results shown in Table 2 indicate the improvement on filter bank performance as the additional criterion of dc leakage free is incorporated in the design. Using multiple objectives our designed filter bank shows a PSNR gain of around 2.5 dB over a wide range of bit rates at the expense of PR violation.
![]()
(a)![]()
(b)![]()
(c)
Figure 4. (a) Original “Boat” Image; (b) Reconstructed image with (8 × 16) NPR CMFB filter bank; (c) Reconstructed image with (8 × 24) NPR CMFB filter bank.
![]()
(a)![]()
(b)![]()
(c)
Figure 5. (a) Original “Barbara” image; (b) Reconstructed image with (8 × 16) NPR CMFB filter bank; (c) Reconstructed image with (8 × 24) NPR CMFB filter bank.
![]()
Table 1. Comparison of different transform’s performance.
![]()
Table 2. Image coding results for “Barbara” image at 0.25 bpp.
5. Conclusion
The design of M-channel uniform cosine modulated filter banks using genetic algorithm is discussed in this paper. The design problem having multiple objectives is solved using non-dominated sorting algorithm with regularity constraint. Although dc leakage free condition is not an essential requirement for image processing in M- channel filter bank as PSNRs don’t improve considerably, its imposition identifies infeasible solutions thereby confines the search for the NPR filter banks simultaneously, and improve visual quality of images at low bit rates. From simulation result, it is shown that the algorithm results in lower tap filters with high stopband attenuation, the least overall distortion and higher coding gain for image compression. Use of progressive image coder based on block-based EZW improves PSNR via reducing blocking and ringing artefacts. The work can be further extended to design of biorthogonal cosine modulated filter banks for image coding application.