Analysis of Flow Estimation Methods for Small Hydropower Schemes in Bua River ()
1. Introduction
Hydropower schemes whether small or large operate upon a reliable resource of water. It is from water where the water or hydro energy is harnessed. Even so, to develop a hydropower scheme you should obtain enough and reliable as well as accurate hydrological information of the catchment or river otherwise the project would be a failure or prove to be both economically and technologically unfeasible. One of the hydrological diagrams which summarize the hydrological characteristic of a river specifically the flow regime of a river or catchment is a Flow Duration Curve (FDC). The FDC is a vital graphic tool in water resources projects particularly hydropower. [1] indicated that the FDC is used for setting the benchmarks for flow regulation and license conditions as well as determining how much water is available for specific use. The role of the FDC in small hydropower poses a big challenge to small hydropower engineers since it is derived from a long term hydrological data which is apparently unavailable. Though it is possible to gauge the rivers for small hydropower plants by deriving the FDCs using the mean annual flow estimation methods, the drawback lies in the uncertainty attached to each of the flow estimation methods since a lot of assumptions are employed.
By understanding the profound importance of these flow estimations, this study was conducted on a well gauged Bua catchment in order to compare the observed/true Bua stream flows against the estimated flows for uncertainty analysis. Since the study was done on a well gauged catchment, a criteria of considering N-1 where N is the number of sites and 1 is the ungauged catchment was employed as the approach of gauging and estimating the stream flows for respective sites.
The Study Area
Bua catchment area covers an area of approximately 10,654 km2 located in the central region of Malawi within the coordinate bearing of 320˚35' and 340˚13'E Longitude and 120˚40' and 120˚55'S Latitude, covering six districts which include Lilongwe, Dowa, Mchinji, Ntchisi, Kasungu and Nkhotakota as described by the Malawi Ministry of Water and Irrigation. Bua catchment is divided into four main sub-catchments with Bua River discharging into Lake Malawi in Nkhotakota district. Figure 1 shows Bua River and the geographical location of the gauging stations under study.
![]()
Figure 1. Bua River and the gauging stations.
2. Methodology
2.1. Hydrological Analysis
2.1.1. L-Moment Homogeneity Analysis
The most important requirement for stream flow estimation methods using the mean annual flows for gauging rivers is that sites must show similar hydrological characteristics. To achieve this requirement this study adopted the L-moment homogeneity analysis approach for regionalization of a homogenous region as described and explained in the book “Regional Frequency Analysis,” [2] . However, there exist additional requirements specifically attached to each flow estimation method and these were also considered in the study.
2.1.2. Discordance Measure
This is an L-moment based statistical data screening approach used to find sites which are grossly discordant from the rest of the sites. The discordance measure referred to as the D-Statistics is computed using the Equation (1). However, the discordance measures for the four gauging stations under study were presented in Table 1 at a D critical value of 1.
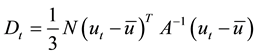 (1)
(1)
where: A is a matrix of sum of squares and cross products: is the mean of L-moment ratios: is a vector of L moment ratios.
[3] suggested a critical value of 3 for N sites greater than 15. The critical value is computed from the following equation:
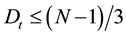 (2)
(2)
2.1.3. L-Homogeneity Test
For testing the regional homogeneity, a test statistic H termed as the heterogeneity measure was suggested [2] . It compares the inter-site variations in sample L-moments for the group of sites with what would be expected of the homogenous region. The inter-site variation of L-moment ratio is measured as the standard deviation of the at-site L-CV’s (L-Coefficient of Variation) weighted proportionally to the record length at each site. To establish what would be expected of a homogenous region, simulations are used [4] . The inter-site variations of each generated region are computed and mean (µv) and the standard deviation, σv of the computed inter-site variation is obtained
The criteria of considering sites or a region heterogeneous is as follows [2] : If H < 1, region is acceptably homogenous: If 1 ≤ H < 2, region is possibly heterogeneous: If H > 2, Region is definitely heterogeneous. The L-moment heterogeneity measure is computed using the following equation:
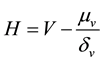 (3)
(3)
where: H = heterogeneity measure: V = the observed dispersion 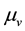 and
and 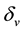 are the simulated regions’ mean and standard deviation respectively.
are the simulated regions’ mean and standard deviation respectively.
The heterogeneity test was done in order to find a homogeneous region. 500 Monte Carlo simulations experiments were conducted for 500 artificial regions in order to compute the heterogeneity measure. The heterogeneity measures of H1, H2 and H3 were 1.79, 1.63 and 0.84 respectively.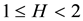 , means possibly heterogeneous; the computed H1 and H2 were between 1 and 2. Therefore it meant that one of the sites was possibly heterogeneous consequently, gauging station 50506 was removed from the region and the heterogeneity test was conducted again. After removing station 50506 the heterogeneity measures of H1, H2 and H3 were 0.77, 0.83 and 0.34 respectively.
, means possibly heterogeneous; the computed H1 and H2 were between 1 and 2. Therefore it meant that one of the sites was possibly heterogeneous consequently, gauging station 50506 was removed from the region and the heterogeneity test was conducted again. After removing station 50506 the heterogeneity measures of H1, H2 and H3 were 0.77, 0.83 and 0.34 respectively.
2.1.4. Goodness-of-Fit Measure and L-Moment Diagram
For a given homogeneous region the goodness-of-fit tests whether a given distribution suitably and closely fits the hydrological data from a given number of candidate distributions. The Generalized Pareto distribution was the best fitting statistical distribution for Bua River flows at a Z-value of 1.09 (see Table 2) and this is also shown by the L-moment diagram below, Figure 2.
![]()
Table 1. Discordance measures of Bua gauging stations at D critical = 1.
![]()
Table 2. The goodness-of-fit measures (at a critical value of 1.64).
![]()
Figure 2. L-moment diagram of sites showing the best statistical distribution that fits the data.
2.1.5. Flow Estimation Methods
Generally there are three main flow estimation methods used in small hydropower which basically use mean annual flows to estimate flow. These three flow estimation used in small hydropower include the runoff data method, the area ratio method and the correlation flow method. Unlike the flow correlation method, when using the runoff data method and the area ratio method the first thing is to compute the mean annual flow (MAF) of the ungauged river. The MAF is computed using equation:
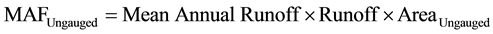 (4)
(4)
The method does not require a gauged site to be located near an ungauged site proposed for the hydropower plant [5] . However, basically the method uses the runoff data which is usually available on runoff maps. Runoff maps can be downloaded online. Therefore, all the three homogeneous sites qualified for the runoff data flow estimation method. The mean annual flow of the ungauged catchment was calculated from the Equation (5) below:
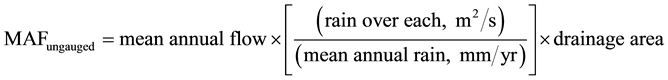 (5)
(5)
Then in order to estimate the flow of the ungauged river, the vertical ordinates 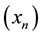 representing the flow duration curve of the gauged stream are multiplied by the ratio of the MAF of the ungauged site/stream to that of the gauged stream/site.
representing the flow duration curve of the gauged stream are multiplied by the ratio of the MAF of the ungauged site/stream to that of the gauged stream/site.
 (6)
(6)
The [5] explains that where the runoff map for the proposed site is not available, the area method becomes useful however, he further advices that a gauged site should exist in the vicinity. On the other hand, he says this method is used upon the assumption that both the ungauged site and the gauged site in the vicinity have similar hydrological characteristics which include: topography, landuse, lithography and geomorphology as well as similar precipitation. Having those similar hydrological characteristics it therefore means that both the gauged and ungauged site have the same runoff values since they have similar parameters that generate the runoff values for rivers and catchments [6] . Subsequently, the mean annual flow will be approximately proportional to the drainage area [5] . The mean annual flow for the ungauged site was estimated using Equation (7) below:
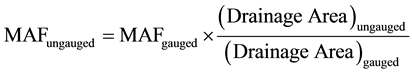 (7)
(7)
Again the flow of the ungauged site was estimated using Equation (6) above.
There exist circumstances when the area of the ungauged site is unknown. The [5] explains that in this case the correlation flow method is best handy. He says this method strictly requires that the gauged site must not be located too far from the ungauged site. Besides, this method demands constant site visits to make occasional stream flow measurement. The method requires and assumes that both the gauged and the ungauged sites display similar precipitation patterns and that their areas, vegetation cover, and geomorphology do not significantly differ [5] .
2.2. Uncertainty Analysis
The study was done on a well gauged catchment for the analysis of flow estimation methods. An overall of three sites gauging stations qualified for uncertainty analysis and bias, accuracy and uncertainty measures for each flow estimation method was computed for all the respective sites/gauging stations and the means for bias, accuracy and uncertainty for the candidate stations were considered as final measures of uncertainty analysis for each respective estimation method. The study was done on a well gauged river in order to validate the uncertainty results by comparing the estimated flows with the original stream flows which have been termed as “true stream flows” in this study. Therefore, the variation pattern between the original flows (true flows) and the estimated flows will be revealed for further inferences and decision making for practitioners’ use. Due to the assumptions for each flow estimation method explained earlier, it is unlikely that all the three gauging stations/sites can qualify for the uncertainty analysis for each and every method apart from the fact that they fall under a homogeneous region. Consequently not all stations qualified among these three stations.
The true stream flows were the true values in the uncertainty analysis of the flow estimations.
Bias (Mean Error), accuracy (RMSE) and standard error (uncertainty) were computed accordingly for each the flow estimation method
The bias was computed from the formula below:
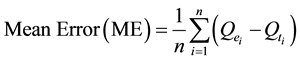 (8)
(8)
where: ![]() and
and ![]() are the estimated stream flow and true stream flow respectively.
are the estimated stream flow and true stream flow respectively.
As one of the important elements in measurement process, just like the bias, accuracy was computed using the formula below:
![]() (9)
(9)
And finally the uncertainty also called the impression expressed as the standard error (Se) which is simply an expectation of the spread of errors was computed using equation as follows [7] :
![]() (10)
(10)
3. Discussion of Results
As suggested by [2] the criteria of judging homogeneity from the heterogeneity measures is that if H < 1; the region is acceptably homogeneous; if 1 ≤ H < 2; the region is possibly heterogeneous; and if H ≥ 2; the region is definitely heterogeneous.
Therefore, in this study station 50506 was removed from the region and a homogeneity test was redone followed by the H1 H2 and H3 values of 0.77, 0.83 and 0.34 respectively. Consequently three stations (50402, 50301 and 50402) were acceptably homogeneous forming a region of similar hydrological characteristics. Therefore, these three qualified for uncertainty analysis of flow estimation methods.
Station 50506 had the lowest mean annual flow with a MAF of 1.05 m3/s. The mean range for station to the rest of the stations which include stations 50401, 50301 and 50402 was 61.66 m3/s which is an outstanding range therefore justifying the homogeneity test results
According to the uncertainty analysis results of this study the, area method for gauging and estimating the stream flows of an ungauged catchment presented the least measures/values of bias accuracy and uncertainty followed by the correlation flows method and the runoff data method presented the largest values of bias accuracy and uncertainty.
Before the study it was hypothetically thought that the runoff data method would present the best/least measures of bias, accuracy and uncertainty since the methods directly uses the mean annual runoff or runoff coefficient data to estimate the mean annual flow of an ungauged river. The mean annual runoff and runoff coefficient are one of the powerful and most-used parameter used to estimate both surface and underground water dynamics and/or flows since they reflect the behavior of a catchment after integrating the most important properties of a catchment that are related to topography and surface cover [6] .
However, both the area method and correction flow methods also demand the prerequisite that both the gauged site and the ungauged site should have similar topographical and surface cover properties. This also makes these two methods as powerful as the runoff data method upon the fact that topography and surface cover of a particular catchment effectively translate the rainfall distribution to a runoff distribution at that particular catchment outlet as explained by David A [5] [6] .
Therefore, the results of this study were confidently accepted as the area method being more accurate, precise and having least values of over/under estimations reflected by the value of bias. The correlation flow method was the second from the area method followed by the runoff data method in terms of bias, accuracy and uncertainty precision.
The [7] express bias as an expectation of over/under prediction based on a statistical model. From the uncertainty analysis results in Table 3, the bias values are all negative values, this means that all estimation methods in this study predicted or estimated values less than the true/observed stream flows. This is also demonstrated in the flow duration curves in Figure 3 that show the estimated FDC below the observed FDC in all gauging stations.
When the gauged and ungauged sites lie in the vicinity to each other and have areas which are not significantly different it is likely that their runoff distributions particularly their runoff magnitudes are similar and therefore the flow estimation output will be more accurate, less biased and considerably precise. For correlation flow method the sites correlated were near to each other and their areas were not significantly different to each other therefore making the correlation flow method more likely powerful than the runoff data method which does not require sites to be near to each other and have area which are not significantly different.
4. Conclusions
From the uncertainty analysis results presented in Table 3, the area method has the lowest measures of bias, accuracy and uncertainty followed by the correlation flows method and lastly the runoff data method. This means that in case of over-or-under estimation (bias), area method is the generated best result followed by the correlation flows method and lastly the runoff method. The other best results are also generated in the same order of the
![]()
Table 3. Uncertainty analysis results.
![]()
Figure 3. The flow duration curves showing estimated flow versus true/ob- served flows.
estimation methods if they are applied in terms of accuracy in case of the agreement of results if repeated estimations are performed under similar assumptions. And finally, uncertainty area method is better than the correlation flow method and lastly the runoff data method. Therefore, the area method is the best flow estimation method to use in small hydropower projects in terms of uncertainty followed by the correlation flow method and lastly the runoff data method.
In all the flow estimation methods, it has been observed that the assumptions appropriate for each method play a very great role in the bias, accuracy and uncertainty of all the methods. If the assumptions are applied appropriately, these flow estimations yield very satisfactory and good results. Besides homogeneity test of the sites particularly using L-moments plays a vital role in the precision, bias and accuracy of the flow estimation methods.
5. Recommendations
One of the problems faced in hydrological modeling and hydropower is the unavailability of hydrological data. This challenge was also encountered in this study particularly in the daily stream flows. There were some missing data in the daily stream flows though the missing values were not many, it is recommended to have at least the best data with most available when specifically conducting uncertainty studies for the best results. However, the degree of missing data was acceptable and it is common to have some missing data in daily hydrological data though the degree of missing data should be limited.
When gauging a river using the flow estimation methods, care should be taken on the assumptions. It is very important to regionalize homogenous sites/catchments before indulging into the task of estimating the flows. L- moments present very satisfactory results as demonstrated in this study.
From the study it was observed that applying the appropriate assumptions for each method correctly, would likely yield very good results in terms of bias, accuracy and uncertainty. Therefore, it was recommended that assumptions regarding each method should be carefully and appropriately applied for good stream flow estimation results.