Inconsistencies in Theoretical Physics, with Focus on the Higgs Mechanism ()
1. Introduction
In recent comments regarding inflation and misinterpretations of BICEP2 [2] data in cosmology, Steinhardt [3] pointed out the claim in [2] that the effects of gravitational waves (generated in the first moments after the Big Bang) had been discovered was not supported by the data and was in fact false. He continued by stating that the incident revealed a serious truth about inflationary theory in cosmology, concluding that the inflationary paradigm is so flexible that it is immune to experimental and observational verification. He further maintained that if inflation is not verifiable, it is therefore scientifically meaningless.
Inconsistencies arise when authors fail to state what they are assuming or do not understand. These arise throughout theoretical physics and go far beyond inflation. In particular, those in particle physics likewise go unnoticed.
One involves the prominent Higgs mechanism [4] -[6] . It was introduced 50 years ago to explain how particles acquire their mass, but at a time when particle physicists assumed that gravity is so weak it can be neglected. However, there is a problem here. Higgs (and colleagues) assumed there was no gravity in order to generate particle mass using spontaneous symmetry breaking (SSB) in the flat Minkowski space of particle physics. But mass is the origin of gravity (curved spacetime in Einstein gravity). The conclusion contradicts the unstated assumption. This is mass without gravity. It is a serious inconsistency, and averting that will be the subject of this discussion.
2. How to Remove the Inconsistency: Introduce Higgs as a Scalar Field in a Scalar-Tensor Theory of Gravity
2.1. This Has Already Been Done
In the afore-mentioned paper [1] on the cosmological constant problem [CCP], this author demonstrated that the cosmological term in Einstein gravity (EG) as a scalar is therefore a potential term―a characteristic of EG that has been noted elsewhere [7] . It was also pointed out in [1] that Brans-Dicke theory is known to have been eliminated experimentally as a scalar-tensor alternative to EG. It was then demonstrated how to construct a consistent scalar-tensor theory in hadron physics to account for the two known values of the vacuum energy density (VED)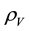 , one inside the hadron as a bag in quantum chromodynamics (QCD), for particle and nuclear physics, and one for the de Sitter phase gravitational background recently observed as an accelerating Universe in Friedman-Lemaitre-Robertson-Walker (FLRW) cosmology [8] -[10] . The two VED states are a consequence of SSB using a Higgs-type mechanism for a hadron potential in a de Sitter space background where the cosmological constant λ is not zero
, one inside the hadron as a bag in quantum chromodynamics (QCD), for particle and nuclear physics, and one for the de Sitter phase gravitational background recently observed as an accelerating Universe in Friedman-Lemaitre-Robertson-Walker (FLRW) cosmology [8] -[10] . The two VED states are a consequence of SSB using a Higgs-type mechanism for a hadron potential in a de Sitter space background where the cosmological constant λ is not zero . Such de Sitter spacetimes where
. Such de Sitter spacetimes where  are referred to as cosmological gravity (CG).
are referred to as cosmological gravity (CG).
It is true that the Higgs has been introduced as the scalar in scalar-tensor gravity in the literature, but not for reasons addressed here. These exceptions are therefore quite by accident. Examples include studies of the Higgs particle in the very early Universe and what role it may have played in inflationary models [11] .
Only this current paper and [1] address the inconsistency in particle physics of comparing energy calculations between incompatible asymptotic spacetimes. It is also argued that de Sitter space or CG is the mandatory background in order to solve the CCP in the observed accelerating Universe where 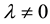 [8] -[10] .
[8] -[10] .
2.2. Cross-Comparison of Killing Charges in Curved Spacetimes: Consistency of Asymptotic States
The Abbott-Deser (AD) method [12] for identifying mass and energy and their Killing-charge successors was shown to be the only consistent means for identifying them as the unique quantities associated with the asymptotic geometry at spatial infinity of de Sitter spacetime [1] . Hence a consistent definition and usage of global energy (Killing charge) in asymptotic spacetime must be adopted in theoretical (particle) physics. Currently, it is ignored; hence, there exists the CCP and other curved background problems.
When one attempts to compare and draw conclusions by cross-comparison of incompatible asymptotic states (with differing Killing charges), infinities arise and the results are an exercise in futility. They also disregard and contradict the known results of the AD method. Such comparisons for typical metrics will be addressed in Section 3 below, illustrating how this process is carried out.
2.3. Doing Quantum Field Theory (QFT) and Particle Physics on Curved Spacetime
Stated differently, there has been a great deal of theoretical work on the unification of gravity with QFT on curved backgrounds, quantum gravity (QG), zero-point energy fluctuations, and our understanding of VED 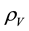 in particle physics as well as cosmology. Furthermore, the difficulties of quantum gravity or performing QFT on curved backgrounds are well-known.
in particle physics as well as cosmology. Furthermore, the difficulties of quantum gravity or performing QFT on curved backgrounds are well-known.
Yet the new requirement in Section 2.2 above follows using an obvious example commonly done in particle physics. Relativistic QFT has pursued VED physics in flat Minkowski space, resulting in the remarkable SSB mechanism used by Higgs et al. Even though EG is nonrenormalizable, its gravitational field 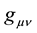 couples minimally and universally to all of the fields of QFT’s renormalizable standard model [13] . To turn on gravity one simply introduces EG along with covariant derivatives in QFT that represent the transition from flat to curved background metrics. This ties everything nicely together except for the gravitational versus flat-space VED problem seen in the CCP. It is inconsistent to compare flat Minkowski space terms, whose metric is not even a solution of EG, with results based upon the metric in CG where
couples minimally and universally to all of the fields of QFT’s renormalizable standard model [13] . To turn on gravity one simply introduces EG along with covariant derivatives in QFT that represent the transition from flat to curved background metrics. This ties everything nicely together except for the gravitational versus flat-space VED problem seen in the CCP. It is inconsistent to compare flat Minkowski space terms, whose metric is not even a solution of EG, with results based upon the metric in CG where . This is now discussed in Section 3.
. This is now discussed in Section 3.
3. De Sitter Space and Particle Physics
Einstein discovered VED in 1917 when he added the cosmological term to his theory of gravitation [14] , and it is possibly his greatest contribution to physics. Only later was it identified as a VED [15] -[17] . Subsequently, it has played a significant role in particle physics, except that EG and  are considered too small to be relevant. Instead, particle physics has become physics without gravity.
are considered too small to be relevant. Instead, particle physics has become physics without gravity.
This section, culled from [1] , will review several of the well-established metrics in CG and relate them to the AD formalism for asymptotic de Sitter spacetimes (where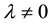 ).
).
3.1. Asymptotic de Sitter Space and the ADT Formalism
The Schwarzschild-de-Sitter metric (SdS) [18] is
 , (1)
, (1)
where
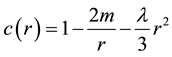 . (2)
. (2)
This curved background represents important global properties that relate to the definition of energy and energy conservation in Einstein gravity. In (1) and (2), we have  with
with 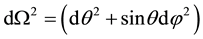 a unit 2-sphere metric, and M the Schwarzschild mass1. The SdS metric (1) becomes Schwarzschild for
a unit 2-sphere metric, and M the Schwarzschild mass1. The SdS metric (1) becomes Schwarzschild for  and de Sitter for
and de Sitter for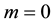 .
.
A canonical formulation of EG as a Hamiltonian system for the simple Schwarzschild case  in (2) was first derived by Arnowitt, Deser, and Misner (ADM) [19] . They determined the ADM energy, momentum, and mass defined by the asymptotic symmetries of (1) and (2) at spatial infinity. Conserved charge (mass, energy, etc.) is associated with a conserved Noether current which is determined by reducing the stress tensor density conservation law
in (2) was first derived by Arnowitt, Deser, and Misner (ADM) [19] . They determined the ADM energy, momentum, and mass defined by the asymptotic symmetries of (1) and (2) at spatial infinity. Conserved charge (mass, energy, etc.) is associated with a conserved Noether current which is determined by reducing the stress tensor density conservation law ![]() in EG to a conserved vector current law using Killing vectors
in EG to a conserved vector current law using Killing vectors![]() . The ADM mass results and is equivalent to the Schwarzschild mass M,
. The ADM mass results and is equivalent to the Schwarzschild mass M, ![]() in (2).
in (2).
For the case of (1) and (2) with![]() , one obtains the Schwarzschild metric which is asymptotically flat as
, one obtains the Schwarzschild metric which is asymptotically flat as![]() . Assuming further that
. Assuming further that ![]() and
and ![]() results in flat Minkowski space. Accordingly, the energy of Minkowski space is zero as expected.
results in flat Minkowski space. Accordingly, the energy of Minkowski space is zero as expected.
Circumstances change significantly, however, when ![]() is re-instated in (2). The full SdS metric (1) is not asymptotically flat and becomes an asymptotic de Sitter space. It is forever distinguished from Minkowski space as
is re-instated in (2). The full SdS metric (1) is not asymptotically flat and becomes an asymptotic de Sitter space. It is forever distinguished from Minkowski space as![]() . With
. With![]() , flat Minkowski space is no longer a relevant background for particle physics because it is not a solution of the Einstein equations [12] , and it is not an asymptotically flat de Sitter space.
, flat Minkowski space is no longer a relevant background for particle physics because it is not a solution of the Einstein equations [12] , and it is not an asymptotically flat de Sitter space.
The ADM approach used above was extended by Abbott and Deser (AD) [12] [20] who proceeded from the ADM results used in the Schwarzschild case and defined the AD Killing charges for the full SdS metric when it asymptotically becomes de Sitter space (dS), in contrast to the asymptotic flat case above. Because of their relevance to CG and the CCP, these AD charges have become very important. That work was later extended by Deser and Tekin (ADT) [21] -[24] who added Weyl and Gauss-Bonnet quadratic curvature terms (scaled by ![]() and
and ![]() respectively) to the Einstein-Hilbert Lagrangian [21] [22] , and found the generalized AD mass to be
respectively) to the Einstein-Hilbert Lagrangian [21] [22] , and found the generalized AD mass to be
![]() , (3)
, (3)
where the term ![]() is the volume of the dS spacetime and has been added to account for the asymptotically pure de Sitter (APdS) case with
is the volume of the dS spacetime and has been added to account for the asymptotically pure de Sitter (APdS) case with ![]() in (2) and (3). Creating an energy density by dividing (3) by
in (2) and (3). Creating an energy density by dividing (3) by![]() , this same term has been found by Padmanabhan [25] using different methods.
, this same term has been found by Padmanabhan [25] using different methods.
The total gravitational energy E of spacetime (3) is well-defined using ADM and ADT methods, provided it is being compared with a metric that has the same asymptotic structure. However, comparison of energies between asymptotically flat Minkowski and asymptotically de Sitter metrics is a misguided exercise. The concepts of global energy and energy conservation become ill-defined when compared to a non-existent solution (Minkowski space) in EG. There is no Einstein gravitational metric ![]() for a Minkowski metric because the latter has no gravity. One must use asymptotic de Sitter spaces to obtain any nonzero E in (3) at all [23] .
for a Minkowski metric because the latter has no gravity. One must use asymptotic de Sitter spaces to obtain any nonzero E in (3) at all [23] .
At this point, one can see from (3) that flat Minkowski space has no asymptotic structure.
3.2. FLRW Cosmological Metric and Asymptotic de Sitter Space
FLRW cosmology is the accepted model for current observations of an accelerating Universe [8] -[10] . Its metric is
![]() , (4)
, (4)
where ![]() is the scale factor and
is the scale factor and
![]() , (5)
, (5)
whose Gaussian curvature ![]() [26] -[28] . Metric (4) is asymptotically an accelerating de Sitter space in its late stages, determined by the cosmological parameter
[26] -[28] . Metric (4) is asymptotically an accelerating de Sitter space in its late stages, determined by the cosmological parameter ![]() as derived from the Einstein-Friedmann equations [28] .
as derived from the Einstein-Friedmann equations [28] .
The global energy of any cosmology, in particular the FLRW case (4), is determined by the ADT charges for APdS spacetime with ![]() in (1), (2), and (3) (no ADM or Schwarzschild mass).
in (1), (2), and (3) (no ADM or Schwarzschild mass).
4. Spontaneous Symmetry Breaking in Scalar-Tensor Theories of Gravity
SSB per se is not due to Higgs et al. [29] [30] . In fact, one of the first examples of the introduction of an SSB potential as a scalar into EG was that of Zee [29] in 1979 (with![]() ). The basic procedure for such scalar- tensor theories with SSB will be reiterated here following that presented in [1] which involves additional terms to include hadron physics in the discussion of the CCP. By setting
). The basic procedure for such scalar- tensor theories with SSB will be reiterated here following that presented in [1] which involves additional terms to include hadron physics in the discussion of the CCP. By setting![]() , the hadron physics disappears in this procedure but consistency is maintained throughout. It is particle physics with gravity.
, the hadron physics disappears in this procedure but consistency is maintained throughout. It is particle physics with gravity.
The Einstein-Hilbert action2 is ![]() which gives the original Einstein field equations
which gives the original Einstein field equations
![]() , (6)
, (6)
with![]() . Since the focus here is on the scalar field
. Since the focus here is on the scalar field ![]() contribution in curved backgrounds, such as the scalar SSB potential
contribution in curved backgrounds, such as the scalar SSB potential![]() , we can begin by discussing a generic Lagrangian using three simple scalar densities:
, we can begin by discussing a generic Lagrangian using three simple scalar densities:![]() ,
, ![]() , and
, and ![]() where
where ![]() represents any of the Lorentz scalar interactions allowable under the inhomogeneous group, although many of these can be introduced by simply re-defining the covariant derivative
represents any of the Lorentz scalar interactions allowable under the inhomogeneous group, although many of these can be introduced by simply re-defining the covariant derivative ![]() in the sense of gauge invariance. Noting that there must also be a kinematic term for the gradient of the scalar field
in the sense of gauge invariance. Noting that there must also be a kinematic term for the gradient of the scalar field![]() , an example of such a general Lagrangian in four dimensions is as follows
, an example of such a general Lagrangian in four dimensions is as follows
![]()
2R is the scalar curvature, ![]() is the Ricci tensor,
is the Ricci tensor, ![]() is the spacetime metric,
is the spacetime metric, ![]() is the energy-momentum tensor, and
is the energy-momentum tensor, and ![]() with
with ![]() where G is Newton’s gravitation constant, c is the speed of light, and
where G is Newton’s gravitation constant, c is the speed of light, and![]() . Also
. Also![]() , and the slash in £ means that
, and the slash in £ means that ![]() (i.e., it is not flat Minkowski spacetime). Typically in particle physics spacetime is flat,
(i.e., it is not flat Minkowski spacetime). Typically in particle physics spacetime is flat, ![]() , and Lagrangians are represented as L.
, and Lagrangians are represented as L.
![]() (7)
(7)
recognizing that ![]() is the cosmological term and is a function of the scalar field
is the cosmological term and is a function of the scalar field ![]() which has zero spin (Spin-0). It actually is a scalar potential function
which has zero spin (Spin-0). It actually is a scalar potential function ![]() which determines the VED or VEDs. Since Lagrangians
which determines the VED or VEDs. Since Lagrangians ![]() are kinetic energy
are kinetic energy ![]() minus potential energy
minus potential energy![]() , (7) can also be written
, (7) can also be written
![]() . (8)
. (8)
To the right-hand-side must be added the source term for matter ![]() that produces
that produces ![]() as the matter contribution to
as the matter contribution to ![]() in (6).
in (6).
4.1. Symmetry-Breaking Potentials ![]()
There are many examples of symmetry breaking potentials![]() . These include the well-known quartic Higgs potential for the Higgs complex doublet
. These include the well-known quartic Higgs potential for the Higgs complex doublet ![]()
![]() , (9)
, (9)
where ![]() and
and![]() . (9) has minimum potential energy for
. (9) has minimum potential energy for ![]() with
with![]() .
.
Treated as a quantum field, ![]() has the vacuum expectation value
has the vacuum expectation value![]() . Following SSB, one finds
. Following SSB, one finds ![]() , indicating the appearance of the Higgs particle
, indicating the appearance of the Higgs particle![]() . In order to determine the mass of
. In order to determine the mass of ![]() one expands (9) about the minimum
one expands (9) about the minimum ![]() and obtains
and obtains
![]() , (10)
, (10)
where ![]() is negative definite and
is negative definite and ![]() acquires the Higgs mass
acquires the Higgs mass![]() .
.
Another example is the more general self-interacting quartic case
![]() , (11)
, (11)
investigated by [31] [32] to examine the ground states of nonminimally coupled, fundamental quantized scalar fields ![]() in curved spacetimes (1) or (4), that will be pursued in Section 4.2 below. (11) is based upon the earlier work of T.D. Lee et al. [33] -[36] and Wilets [37] [38] for modelling the quantum behavior of hadrons.
in curved spacetimes (1) or (4), that will be pursued in Section 4.2 below. (11) is based upon the earlier work of T.D. Lee et al. [33] -[36] and Wilets [37] [38] for modelling the quantum behavior of hadrons.
![]() is arbitrary and represents a cosmological term in all cases, and all are unrelated except that they represent the VED or VEDs of the associated scalar field. The terms in
is arbitrary and represents a cosmological term in all cases, and all are unrelated except that they represent the VED or VEDs of the associated scalar field. The terms in ![]() have a mass-dimension of four as required for renormalizability. In the case of (9)-(10), it is the addition of the Higgs scalar
have a mass-dimension of four as required for renormalizability. In the case of (9)-(10), it is the addition of the Higgs scalar ![]() that makes the standard electroweak theory a renormalizable gauge theory. Also, the electroweak bosons acquire the mass
that makes the standard electroweak theory a renormalizable gauge theory. Also, the electroweak bosons acquire the mass ![]() as a result of their interaction with the Higgs field
as a result of their interaction with the Higgs field ![]() if it is present in the vacuum.
if it is present in the vacuum.
A variation of (11) was used in [1] to address hadrons, which exhibit two VEDs (Figure 1 in [1] ), by establishing the direct relationship between Einstein’s λ and the hadron theory of Friedburg, Lee, and Wilets (FLW) where (11) becomes ![]()
![]() , (12)
, (12)
with ![]() representing a self-interacting hadron scalar
representing a self-interacting hadron scalar ![]() -field whose scaling coefficients are to be determined.
-field whose scaling coefficients are to be determined.
4.2. Consistency Follows upon Definition of the Energy-Momentum Tensor for Matter
The task now is to complete the scalar-tensor picture beginning with (6). The total Lagrangian ![]() for the action involved must merge gravity with matter as
for the action involved must merge gravity with matter as ![]() being the sum of gravity, matter, and their interaction term
being the sum of gravity, matter, and their interaction term![]() . At this point, the Einstein-Hilbert action giving rise to (6) is extended to include the scalar field
. At this point, the Einstein-Hilbert action giving rise to (6) is extended to include the scalar field ![]() used in (12) with
used in (12) with ![]() and λ encompassed into
and λ encompassed into ![]() as
as ![]() where B is the well-known VED in QCD, Yang-Mills, and FLW hadron theory. This is accomplished by introducing the scalar-tensor action of Jordan-Fierz-Brans-Dicke (JFBD) [39] -[41]
where B is the well-known VED in QCD, Yang-Mills, and FLW hadron theory. This is accomplished by introducing the scalar-tensor action of Jordan-Fierz-Brans-Dicke (JFBD) [39] -[41]
![]() , (13)
, (13)
where ![]() is a function of the
is a function of the ![]() -field, and
-field, and ![]() in (6) is likewise as
in (6) is likewise as![]() . For purposes here, the original JFBD ansatz
. For purposes here, the original JFBD ansatz ![]() is adopted although there are others. Note that special care must be given throughout to
is adopted although there are others. Note that special care must be given throughout to ![]() which has five degrees of freedom (DOFs) with Spin-0, Spin-1, and Spin-2 states of spin, discussed in [1] App. A-4, in addition to the scalar Spin-0
which has five degrees of freedom (DOFs) with Spin-0, Spin-1, and Spin-2 states of spin, discussed in [1] App. A-4, in addition to the scalar Spin-0 ![]() -field.
-field.
The field Equations (6) are now transformed, with the energy momentum tensor ![]() begin represented by a matter and a potential contribution, where
begin represented by a matter and a potential contribution, where ![]() contributes to the
contributes to the ![]() -field tensor
-field tensor![]() . The matter tensor is the original tensor
. The matter tensor is the original tensor ![]() in (6), and their sum
in (6), and their sum ![]() is conserved by the Bianchi identities:
is conserved by the Bianchi identities:
![]() , (14)
, (14)
![]() , (15)
, (15)
![]() . (16)
. (16)
(16) resolves the mass dimensionality of ![]() and B in that both sides of the equation have mass dimension two.
and B in that both sides of the equation have mass dimension two.
Recalling that the Lagrangian for the FLW hadron model ![]() is that for QCD (quarks
is that for QCD (quarks ![]() pluscolor
pluscolor![]() ) supplemented by the nonlinear
) supplemented by the nonlinear ![]() -field
-field ![]() and a quark-
and a quark-![]() mixing term
mixing term![]() , we have
, we have
![]() (17)
(17)
The ![]() term will become the
term will become the ![]() -field interaction term with scalar-tensor gravity
-field interaction term with scalar-tensor gravity ![]() in the total Lagrangian that includes a nonminimally coupled Einstein-Hilbert term
in the total Lagrangian that includes a nonminimally coupled Einstein-Hilbert term ![]() in (13) as
in (13) as
![]() , (18)
, (18)
with
![]() . (19)
. (19)
![]()
3To recover the pure Higgs mechanism with gμν, set ![]() and use (9) rather than (11) or (12). This is for pedagogical purposes only because λ actually has two VED states, one for cosmology and one for hadrons and QCD. Hence, the procedure has no physical basis.
and use (9) rather than (11) or (12). This is for pedagogical purposes only because λ actually has two VED states, one for cosmology and one for hadrons and QCD. Hence, the procedure has no physical basis. ![]() cannot be ignored in particle physics.
cannot be ignored in particle physics.
The ![]() -field, again, is the scalar field of the scalar-tensor gravity presented here, giving a scalar field that couples to QCD in the FLW hadron model. Lee [42] has noted that QCD has no scalar field except for gluon and color condensates arising from nonlinear interactions of the color fields
-field, again, is the scalar field of the scalar-tensor gravity presented here, giving a scalar field that couples to QCD in the FLW hadron model. Lee [42] has noted that QCD has no scalar field except for gluon and color condensates arising from nonlinear interactions of the color fields![]() . Regardless of its origin and composition, this scalar is the basis for the scalar-tensor model under discussion3.
. Regardless of its origin and composition, this scalar is the basis for the scalar-tensor model under discussion3.
The terms in (17) appearing in (18) involve quarks![]() , scalar
, scalar![]() , and colored gluons
, and colored gluons![]() , which are defined as
, which are defined as
![]() , (20)
, (20)
![]()
![]() , (21)
, (21)
![]() , (22)
, (22)
with counter terms not shown. ![]() is the
is the ![]() -quark coupling constant,
-quark coupling constant, ![]() the strong coupling,
the strong coupling, ![]() the non- Abelian gauge field tensor,
the non- Abelian gauge field tensor, ![]() the quark flavor mass matrix,
the quark flavor mass matrix, ![]() the gauge-covariant derivative, and
the gauge-covariant derivative, and ![]() the gravitation-covariant derivative (also in
the gravitation-covariant derivative (also in![]() ) with the spin connection derivable upon solution of (14) above, defining the geodesics.
) with the spin connection derivable upon solution of (14) above, defining the geodesics. ![]() is the phenomenological dielectric function introduced by Lee et al. [34] , where
is the phenomenological dielectric function introduced by Lee et al. [34] , where ![]() and
and ![]() in order to guarantee color confinement. The SU3 Gell-Mann matrices and structure factors are
in order to guarantee color confinement. The SU3 Gell-Mann matrices and structure factors are ![]() and
and![]() .
.
Using (18)-(21), variation of (17) which neglects gravity in (18), gives the FLW equations of motion for σ and![]() ,
,
![]() , (23)
, (23)
![]() , (24)
, (24)
when one neglects the gluonic contribution (21). ![]() is the curved-space Laplace-Beltrami operator, and
is the curved-space Laplace-Beltrami operator, and ![]() is
is
![]() . (25)
. (25)
Now we can turn to the energy-momentum tensor ![]() in (15). It is comprised of two terms. The first is the usual matter contribution
in (15). It is comprised of two terms. The first is the usual matter contribution ![]() which includes all matter fields in the Universe except gravitation,
which includes all matter fields in the Universe except gravitation,
![]() , (26)
, (26)
![]()
4In (26),![]() .
.
and is independent of the gravitational ![]() -field4. The second term in (15)
-field4. The second term in (15) ![]() is new and must include the effects of
is new and must include the effects of ![]() in (19). Introducing a superscript “R” for renormalizable and consolidating all of the
in (19). Introducing a superscript “R” for renormalizable and consolidating all of the ![]() terms, we have in short-hand derivative notation
terms, we have in short-hand derivative notation
![]() . (27)
. (27)
Based upon (26) and (27), variation of (13) will now give the final equations of motion. In order not to sacrifice the success of the principle of equivalence in Einstein’s theory [13] , a Brans-Dicke assumption must also be made. Only ![]() and not
and not ![]() enters the equations of motion for matter (consisting of particles and photons). The interchange of energy between matter and gravitation thus must follow geodesics as assumed by Einstein [43] . The energy-momentum tensor for matter is hence assumed to be conserved in the standard fashion,
enters the equations of motion for matter (consisting of particles and photons). The interchange of energy between matter and gravitation thus must follow geodesics as assumed by Einstein [43] . The energy-momentum tensor for matter is hence assumed to be conserved in the standard fashion,![]() .
.
The derivation of ![]() is a textbook problem
is a textbook problem ![]() [43] with specific details given in [1] where
[43] with specific details given in [1] where ![]() since that is the case here. Also, the potential
since that is the case here. Also, the potential ![]() is present with its renormalization restrictions in (12) being unique to this more thorough case.
is present with its renormalization restrictions in (12) being unique to this more thorough case.
The most general symmetric tensor of the form (27) which can be built up from terms each of which involves two derivatives of one or two scalar ![]() -fields, and
-fields, and ![]() itself, is
itself, is
![]() (28)
(28)
where the coefficients A, B, C, D, and E are to be found. Taking the covariant divergence of (27), recalling the ansatz![]() , taking the trace of (14) and (15) for
, taking the trace of (14) and (15) for![]() , modifying (22) to include the gravitational coupling with
, modifying (22) to include the gravitational coupling with ![]() (still assuming
(still assuming![]() ) to produce the trace for
) to produce the trace for![]() , and obtaining the remaining trace
, and obtaining the remaining trace ![]() from (38), the desired energy-momentum tensor for the
from (38), the desired energy-momentum tensor for the ![]() -field follows as
-field follows as
![]() , (29)
, (29)
with ![]() and
and![]() .
.
Inserting (29) into (14) and (15) gives the full field equations
![]() , (30)
, (30)
while putting (29) into the trace ![]() yields the scalar wave equation (with
yields the scalar wave equation (with![]() ) for the
) for the ![]() -field
-field
![]() , (31)
, (31)
where ![]() is the source of
is the source of ![]() -coupling to the traditional trace
-coupling to the traditional trace ![]() in JFBD theory. There is now coupling to the trace
in JFBD theory. There is now coupling to the trace ![]() in (31) compared to (23). If
in (31) compared to (23). If![]() , (30) is a conformally mapped set of Einstein field equations.
, (30) is a conformally mapped set of Einstein field equations.
From the SSB potential ![]() in (12), we see that a has mass-dimension two or
in (12), we see that a has mass-dimension two or![]() . By taking the derivative
. By taking the derivative![]() .
.
![]() , (32)
, (32)
along with (31), the ![]() -field has acquired mass
-field has acquired mass
![]() . (33)
. (33)
Therefore it is a short-range field with only short-range interaction. (31) can be re-written
![]() . (34)
. (34)
After moving the ![]() term to the left-hand side,
term to the left-hand side, ![]() is the remainder of (32) and a wave equation results. Hence a static solution for the
is the remainder of (32) and a wave equation results. Hence a static solution for the ![]() -field must have a Yukawa cutoff
-field must have a Yukawa cutoff ![]() where
where![]() .
.
4.3. Interpretations of the Scalar Field
The interpretation of the scalar field arising from the well-known quartic Higgs potential for the Higgs complex doublet ![]() in (9) is legendary, having made the standard model of particle physics renormalizable. Its possible discovery at CERN is significant for particle physics without gravity.
in (9) is legendary, having made the standard model of particle physics renormalizable. Its possible discovery at CERN is significant for particle physics without gravity.
The discussion here, however, has shown such a treatment to be inconsistent and certainly incomplete in spite of years of speculation in the literature about “Higgs gravity”. Nevertheless, one feature of discussions regarding the Higgs boson addresses its quality of giving some particles their mass (not all of them, just those in the standard electroweak model). Figuratively speaking, these particles acquire their mass by interacting with the universal background Higgs field ![]() in (9).
in (9).
In the discussion here, the cosmological de Sitter background with a cosmological constant ![]() acts to give particles and photons an effective “mass” in the sense that they must follow geodesics in the curved spacetime of de Sitter space rather than flat trajectories in Minkowski space. The interaction is with the curved CG background, and the metaphors are related.
acts to give particles and photons an effective “mass” in the sense that they must follow geodesics in the curved spacetime of de Sitter space rather than flat trajectories in Minkowski space. The interaction is with the curved CG background, and the metaphors are related.
Furthermore, there exist two Spin-0 degrees of freedom in a scalar-tensor theory of gravity. As mentioned in Section 4.2, special care must address these DOFs in order to guarantee that the combined Spin-0, Spin-1, and Spin-2 states of spin do not create negative energy modes and instabilities, as discussed in [1] App. A-4.
There is an additional problem, involving the fact that the SSB mechanisms addressed in the scalar (Spin-0) potentials (9)-(12) are different mechanisms. Future work is necessary to explain why there would be two different SSB events in the vacuum such as (9) and (12). That subject lies far beyond the point of the present discussion. One naïve resolution to this quandary is simply to set the ![]() -field mass
-field mass ![]() in (34) to the value measured at CERN,
in (34) to the value measured at CERN, ![]() [44] -[47] .
[44] -[47] .
5. Conclusions
The point of this analysis has been to demonstrate the procedure for introducing SSB mechanisms for scalar Spin-0 fields into scalar-tensor theories of gravity in a consistent fashion. This procedure has been careful to treat particle physics on an asymptotic FLRW cosmology representing an accelerating Universe [8] -[10] with cosmological constant ![]() using scalar-tensor gravity coupled to FLW hadron physics. That includes quarks and gluons in particle physics, as well as known VED states for the scalar field. Furthermore, it complies with the compatibility of asymptotic spacetime structure implied by the ADT formalism presented in Section 3.
using scalar-tensor gravity coupled to FLW hadron physics. That includes quarks and gluons in particle physics, as well as known VED states for the scalar field. Furthermore, it complies with the compatibility of asymptotic spacetime structure implied by the ADT formalism presented in Section 3.
The Higgs et al. mechanism [4] -[6] accomplishes none of this. It is particle physics without gravity in flat Minkowski space, and cannot be reconciled with Einstein gravity except through some procedure as that proposed here. The statements by Damour [13] to the effect that all one has to do is “turn on” ![]() using the Einstein-Hilbert action (mentioned in Section 2.3) is incorrect because that common misperception does not necessarily comply with the requirement for compatibility of asymptotic spacetime structure in Section 3. The gravitational background must asymptotically be a de Sitter space as in FLRW cosmology due to the physical measurement of an accelerating Universe where
using the Einstein-Hilbert action (mentioned in Section 2.3) is incorrect because that common misperception does not necessarily comply with the requirement for compatibility of asymptotic spacetime structure in Section 3. The gravitational background must asymptotically be a de Sitter space as in FLRW cosmology due to the physical measurement of an accelerating Universe where ![]() [8] -[10] . This was also argued with respect to solving the CCP in [1] .
[8] -[10] . This was also argued with respect to solving the CCP in [1] .
Based upon the arguments presented here, the Higgs mechanism at best is incomplete. Its popularity has become folklore, but folklore is scientifically meaningless. Much in physics today is actually metaphysics5, examples of which are principles and assumptions such as the principle of relativity, the Pauli exclusion principle, or multiverses. These cannot be measured or proven experimentally. The first two are articles of faith that always seem to work. They are beyond physics yet they are used every day. The third is not observable.
On the other hand, inconsistencies that persist often become folklore and are also scientific meaningless. These are an artifact of misunderstanding some portion of physics, or they are based upon commonplace human error.
As long as particle physics has little or no respect for the asymptotic structure of curved spacetime discussed in Section 3, the inconsistency problem addressed here will go unresolved as will the CCP. A consistent treatment of VED in both cosmological gravity and particle physics is necessary. The scalar-tensor theory presented here may certainly be incomplete, but it is not inconsistent.
NOTES
1In general, natural units ħ = c = 1, metric signature (−, +, +, +), and a 4-dimensional spacetime are assumed.
![]()
5In Newton’s time there was natural philosophy which consisted of physics and metaphysics. Physics pertains to that which can be experimentally observed and corroborated with measurements while metaphysics is that portion which cannot and therefore lies beyond physics.