Identification of Influential Sea Surface Temperature Locations and Predicting Streamflow for Six Months Using Bayesian Machine Learning Regression ()
1. Introduction
Streamflow depends on the distribution of precipitation in time and space which further depends on the climatic conditions. Shivakumar [1] observed that the monthly and annual streamflow series are affected by long-term climate. The atmospheric and hydrologic sciences have recently used sea surface temperature (SST) to predict streamflow variability [2] -[4] . SST is an indicator of oceanic-atmospheric circulation and has important consequences on the weather around the globe. SST has strong link with the hydrology of the river basin which provides the predictive information about the hydrologic variability [5] . Identification of an appropriate location of SST is likely to improve the predictive ability of the model. Therefore input of climatic conditions in the model through SST has a significant importance.
The precise information about the quantity of water availability in the next season can be very useful for the agricultural planning, watershed management, and other decision making processes [6] . It can benefit the management of water resources, in particular allowing decision on water allocation for irrigations [7] -[9] and other purposes. Financial commitment made by the farmers early in the season can result in substantial economic losses if the resulting seasonal flow does not subsequently supply enough irrigation water. Forecast with long- lead time facilitates co-ordination between different system users that may be important in multiple-use water resource systems [10] .
Machine learning regression model has been used as an alternative to physically based models. The complexities in the physically-based models and difficulties associated with the data acquisitions and corresponding expenses that these models would require have limited the application of such models. Machine learning models are good at capturing the underlying physics of the system by relating input and output. They are robust and are capable of making reasonable predictions using historical data [11] . Artificial Neural Network (ANN), Support Vector Machine (SVM), and Relevance Vector Machine (RVM) are few popular machine learning models. The disadvantage of the ANN model is that it may get stuck in local minima rather than global minima. The SVM model is a popular machine learning model [12] however this model makes unnecessary liberal use of the basis function. In the SVM model, the number of support vectors grows linearly with the size of data [13] . In addition, the SVM predictions are not probabilistic. The RVM is a Bayesian machine learning model. This is sparser than the SVM model and gives probabilistic output as well. Optimizing model parameter for the RVM model is relatively easier, however the performance is comparable. The RVM model has been successfully used by many past researches for water resources operation and management works [3] [14] . The RVM model is therefore proposed in this study. The objective of this study is to identify the best locations of SST for the selected locations of unimpaired stream gages (except one), and use them for the streamflow prediction.
2. Materials and Methods
2.1. Study Area
Five stream gages were selected at different locations of Utah which spatially covers the state from north to south (Figure 1). For most of the stream gages, the flows were not affected by diversion or regulation and the long year of systematic records were available. For Sixth Water Creek, the flow however, was partly affected by diversion until 2004. Two sites were chosen from northern region (Weber River near Oakley and Chalk Creek at Coalville), two from central region (Muddy Creek near Emery and Sixth Water Creek near Springville), and one from the southern region (Sevier River at Hatch) of the state. Snow accumulation and melt is a very significant feature in terms of annual hydrologic cycle for these streams [15] . Table 1 shows the basin area, length of stream, and location of stream gages used in this study.
2.2. Relevance Vector Machine
Relevance Vector Machine is a supervised learning model based on sparse Bayesian learning. This is a model of identical functional form to the SVM developed by Vapnik [16] [17] .
For the given input-target pair 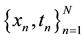 in training data set, the model learns a dependency of the targets (streamflow in this study) on the inputs (e.g. SST, snow and temperature data) with the objective of making accurate predictions of the target (t) for previously unseen values of input x [13] [18] .
in training data set, the model learns a dependency of the targets (streamflow in this study) on the inputs (e.g. SST, snow and temperature data) with the objective of making accurate predictions of the target (t) for previously unseen values of input x [13] [18] .
Target 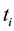 is a sample from the model
is a sample from the model 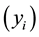 with additive noise
with additive noise 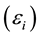 which has mean zero with variance s2 [13] .
which has mean zero with variance s2 [13] .
![]()
Figure 1. Location of the stream gages and SnoTel stations.
![]()
Table 1. Geometric characteristic of stream gages.
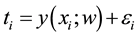 (1)
(1)
The unknown function y is the product of design matrix (F) and weight parameter (w). In the vector form, Equation 1 can be written as,
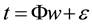
where the target and weight vector are expressed as  and
and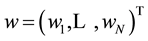 , respectively. An independent Gaussian noise is assumed. Thus,
, respectively. An independent Gaussian noise is assumed. Thus, 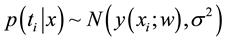 and the likelihood of complete dataset is written as,
and the likelihood of complete dataset is written as,
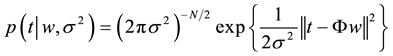 (2)
(2)
The maximum likelihood estimate of w and s2 in Equation 2 may suffer from over fitting [13] . To avoid this, w is constrained with mean zero Gaussian prior probability, which results in majority of w being zero. This constrain makes the RVM model sparser than the SVM model [13] . The posterior covariance and mean of w, estimated from Bayes’ rule [13] are 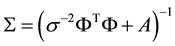 and
and 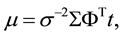 respectively, and
respectively, and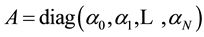 , where α is uniform hyperpriors and diag (...) is a diagonal matrix. The α and
, where α is uniform hyperpriors and diag (...) is a diagonal matrix. The α and  are estimated from an iterative re-estimation formula [13] given by,
are estimated from an iterative re-estimation formula [13] given by,
![]() (3)
(3)
where![]() . The term
. The term ![]() is the ith posterior mean weight and N is the number of data examples (length of data set). The
is the ith posterior mean weight and N is the number of data examples (length of data set). The ![]() is ith diagonal element of the posterior weight covariance computed with the current a and
is ith diagonal element of the posterior weight covariance computed with the current a and![]() . The learning algorithm proceeds by iterative process of Equation (3) together with updating the posterior statistics S and m, until suitable convergence criteria is satisfied [13] .
. The learning algorithm proceeds by iterative process of Equation (3) together with updating the posterior statistics S and m, until suitable convergence criteria is satisfied [13] .
The predictions for new input ![]() are made based on the posterior distribution over the weights, conditioned on the maximizing values
are made based on the posterior distribution over the weights, conditioned on the maximizing values ![]() and
and![]() .
.
![]()
where![]() ,
, ![]() , and
, and ![]() is a basis function. Further details of the RVM model can be found in Tipping [13] [18] . The model used in this study is one introduced by Thayananthan [19] . This is a Bayesian regression tool extension of the RVM algorithm developed by Tipping and Faul [20] . Gaussian kernel was used in this study as it has shown to perform better than other kernels [21] [22] .
is a basis function. Further details of the RVM model can be found in Tipping [13] [18] . The model used in this study is one introduced by Thayananthan [19] . This is a Bayesian regression tool extension of the RVM algorithm developed by Tipping and Faul [20] . Gaussian kernel was used in this study as it has shown to perform better than other kernels [21] [22] .
2.3. Model Formulation
The model (Equation (4)) consists of predicting total volume of water passing the stream gage for next six months. Inputs to the model are past streamflow data, snow water equivalent and SnoTel temperature of nearby SnoTel stations and SST. The input variables are selected based on the underlying physical processes and climatic factors that influence the generation of streamflow.
![]() (4)
(4)
where ![]() is a total volume of water flowing through the gage in last six months,
is a total volume of water flowing through the gage in last six months, ![]() and
and ![]() are the average SWE and SnoTel temperature calculated over the last twelve months,
are the average SWE and SnoTel temperature calculated over the last twelve months, ![]() represents 12 months previous monthly average sea surface temperature value. The output
represents 12 months previous monthly average sea surface temperature value. The output ![]() is the volume of water passing the stream gage for next six months.
is the volume of water passing the stream gage for next six months.
Smith and Reynolds SST were used in this study which covers majority of world’s ocean by 2˚ by 2˚ grid [23] . Six locations were selected from the Pacific and Atlantic oceans. They were North Pacific (NP), Central Pacific (CP), Tropical Pacific (TP), East Atlantic (EA), Middle Atlantic (MA) and Tropical Atlantic (TA) (Figure 2).
In Utah, snow is an important variable affecting the discharge in the stream. When the precipitation falls as snow, it settles, compacts and melts several months later and is prominent source of streamflow [24] . Snow serves as storage of water especially in the western US which has major effect on the streamflow in the spring and early summer months. Snow Water Equivalent (SWE) is a common term used in the hydrological modeling which is defined as equivalent depth of water when snow completely melts. SWE data are collected from the nearby SnoTel stations. Use of SWE data from more than one SnoTel stations improves prediction as it incorporates SWE spatial variability [2] . Harris Flat and Midway Valley SnoTel stations were used for Sevier River at Hatch, Smith and Morehouse and Chalk#1 were used for Weber River near Oakley, Chalk#1 and
![]()
Figure 2. The locations for the sea surface temperature (from Khalil et al. [3] ).
Chalk#2 were used for Chalk Creek at Coalville, Buck Flat and Dill’s Camp were used for Muddy Creek near Emery and Strawberry Divide was used for Sixth Water Creek near Springville. Although some SnoTel sites were physically outside of the watershed, they were still included in the model due to their strong correlation with the streamflow processes. The SWE data were collected from Natural Resource Conservation Service (NRCS) (http://www.wcc.nrcs.usda.gov/snow). The period of 1980-2009 was used in this study because of the relative completeness of data in the basins for these years.
Temperature affects the melting rate of snow which consequently affects the discharge in the stream. The high discharge in the spring and early summer month is due to rising temperature when there is enough snowpack in the watershed. The temperature data were also collected from the SnoTel stations operated by NRCS and the period of data collection for local temperature was same as that of SWE.
The model was trained for 1980-2001 and tested on 2002-2009 for Weber River near Oakley, Chalk Creek at Coalville, and Muddy Creek near Emery. The Sevier River at Hatch was trained for 1982-2001 and tested for 2002-2009 while the Sixth Water Creek near Springville was trained for 2000 to 2006, and tested for 2007 to 2009. For the SST value, an individual as well as combinations of the SSTs were used for developing the best model. The best model was selected based on the test statistics (RMSE and Nash-Sutcliffe efficiency in the test phase).
3. Results and Discussion
3.1. Identification of Influential Sea Surface Temperature Locations and Prediction of the Volume of Water Passing the Gage for Next Six Months
The test statistics were computed for each individual SST for the volume of water passing through the stream gage for next six months. The SST locations that developed the best test statistics are shown in Figure 3.
A 95% confidence interval for the median RMSE is shown in Table 2. The test RMSE from the best identified SST locations is outside of the 95% confidence interval. This indicates that the test RMSE from the best SST location is significantly better than the test RMSE from the other SST locations. The summary results of the best SST locations for each stream gage are shown in Table 3.
Using the best SST locations, the volume of water passing through each selected stream gage was predicted (Figure 4). A good match between actual and predicted flow volume was obtained. The plot of predicted versus actual flow volume saturates about the bisector which indicates that the model prediction is close to actual values (Figure 4). The accuracy of the prediction was high for the unimpaired gages while it was relatively less for impaired gage (Sixth Water Creek near Springville). In general cases, the model has perfectly captured the high flow but the low flow was not captured accurately. Since the inputs representing the groundwater flow were not included in the model, this level of discrepancy is obvious. The overall prediction shows that the model is accurate and can be used for predicting six months ahead streamflow volume. The uncertainty of prediction was captured by confidence interval in the test phase for each gage.
The illustration about the best location of SST for the given location of stream gage is discussed below. When monthly data are used, the data consists of seasonal, annual, and inter-annual components. The effect of seasonal
![]()
Figure 3. Locations of the sea surface temperature that developed the best test statistics for volume of water passing the stream gage for next six months.
![]()
Table 2. The 95% confidence interval of the median RMSE.
![]()
Table 3. Summary of best test result for volume of water passing the gage for next six months.
component is stronger than other components for the monthly data. However, when the variables were cumulative or averaged over the time for the model (Equation (2)), the seasonal component gets eliminated. The remaining components are annual to interannual components, which are low frequency components. North Pacific SST has low frequency component (annual, interannual to interdecadal) so it is obvious to have NP SST influencing more than any other SST locations for most of the streamflow sites in Utah for the volumetric predictions. This includes Chalk Creek at Coalville, Muddy Creek near Emery, Sixth Water Creek near Springville and Sevier River at Hatch. When monthly data were used, the best prediction was obtained from TP SST for Sevier River at Hatch, however, when predictions were made for the volume of water passing through the streamflow site, the variables were averaged or cumulative over the time. The seasonality effect was thus eliminated leaving low frequency components. These components were best represented by the NP region. Therefore, the best predictions were obtained from NP SST. This result is consistent with the result obtained by Asefa et al. [2] .
For Weber River near Oakley, the combination of CP, NP, and TP developed the best model. However, this result was very close to prediction from the combination of NP and CP SST. The principal moisture source of this area is Pacific Ocean. In addition, this stream gage is outside of the ENSO dominance region. There is no seasonality component, therefore NP and CP SST appeared to be the most important inputs.
3.2. Generalization and Robustness of Model
The bootstrap analysis is a data-based simulation method for statistical inference [25] and gives the estimate of measure of variability of test statistics with the change in training data. We used bootstrap in this study to test the robustness and generalization ability of the model. For each stream gage, bootstrap analysis was performed and the test statistics were computed for each bootstrap sample. The narrow bound of histogram showed that the model was robust (Figure 5 and Figure 6). The dotted red line in the figures shows the 2.5th percentile and 97.5th percentile values of the test statistics. This plot confirms that the model is robust and is accurate to use as a long-term streamflow prediction model.
4. Conclusions
The Relevance Vector Machine successfully transformed the input variables (sea surface temperature, local
meteorological conditions, and SWE) into reasonably accurate forecasting of streamflows for next six months. For each gage, the best location of SST was identified. It was found that the SST of Pacific Ocean predicted better than that of Atlantic Ocean because this region represents the majority of Ocean-atmosphere climate influence in the western U.S. [26] [27] . NP SST was the best location of SST for most of the stream gages in Utah for the prediction of volume of water passing the gage for next six months.
The prediction results were highly accurate for unimpaired stream gages while the accuracy was satisfactory for the impaired gage (Sixth Water Creek near Springville). Since the human induced effects were not incorporated in the model for impaired gage, it is obvious to have less efficiency compared to the unimpaired gages. The model has predicted the streamflow perfectly for high flow but low flows were not captured perfectly. The overall predictions were, however, accurate and had good agreement with the observed streamflow values. The uncertainty of the predictions was also captured and presented by the confidence interval. The reliability and robustness of the model were tested from the bootstrap analysis. This analysis confirmed the good predictability and robustness of the model.
This study has demonstrated that with the use of appropriate input, the RVM model can be utilized for the successful forecast of the long-term streamflow. Accurate and reliable long-term streamflow prediction is crucial for the management of water resources in the basin scale. This information could help the water managers and stakeholders for the planning and decision making of the water resources which ultimately reduces the financial risk associated with the water users to future water shortages.
NOTES
*Corresponding author.