Measuring the Qatar-Kazeron Fault Dip Using Random Finite Fault Simulation of September 27, 2010 Kazeron Earthquake and Analytical Signal Map of Satellite Magnetic Data ()
1. Introduction
In the past decades, many earthquakes have occurred in dextral strike-slip fault systems in the Persian Gulf Coast and Dezful Embayment. Results of modeling wave shapes and micro-studies on earthquakes suggest that most earthquakes occurring the in south of Iran have a depth of below 30 km (Barbarian). Strong ground motion simulation is a means of accelerogram-based study of earthquakes. This method is particularly useful for estimation of strong ground motion parameters of areas with no available information. Strong ground motion is a parameter of high important to the design and reinforcement of structures. This area is located in the west of Fars Province and embraces the Kazeron rock fault. Recently, several relatively important earthquakes have occurred in these areas. This area houses the main Kazeron fault. The September 27, 2010 Kazeron Earthquake, which occurred at 14:52:46 with a magnitude of Ml6.1 and Mw5.8 (BHRC), influenced a large part of Fars and Bu- shehr provinces. The epicenter calculated based on the time difference between the records of waves P and S on the accelerograms, had latitude of 29.78N and longitude of 51.76E.
At the time of preparing this report, 27 accelerograms were obtained from the accelerometer stations in Fars, Bushehr, and Kohgiluyeh and Boyer-Ahmad provinces. According to the report data, the highest acceleration recorded in Qaemieh Station, which is the closest to the earthquake focus (hypocenter), was about 335 cm/s2 (unmodified acceleration) on the horizontal component. The maximum vertical acceleration recorded in this sta- tion was also 103 cm/s2. Kazeron station reported an acceleration of app. 117 cm/s2 on the horizontal compo- nent.
Demonstration of magnetic properties by different elements, compounds and minerals is closely associated with the electron configuration of the constituent elements [1] . Atoms and ions contain charged particles moving fast. Moreover, the spinning and rotational motion of electrons with negative charge inside orbitals is higher when they move [2] . Since in every fully occupied orbital two electrons spin and rotate in opposite directions, the effect of magnetic moment inside the orbital is zero. Hence, the effective magnetic moment of an atom or ion depends on its semi-occupied orbitals. Therefore, compounds containing the transition elements of the periodic table are magnetic and rocks are attracted to magnetic fields. For example, elements such as iron and nickel are highly attracted to magnetic fields. In resolution-based magnetic remote sensing studies satellite magnetic data was used. Image processing and filtering plays an important role in the interpretation of magnetic data [3] . In the interpretation of magnetic remote sensing data, removal of regional effects and local anomalies associated with subsurface shallow constructions increases the resolution of deep structures.
Qatar-Kazeron north-south fault with the length of 450 km is rock foundation and a large part of it covered by young quaternary alluvium, that this causes the structures and fractures coating in the bedrock. Since residential areas are located mainly in the plains including Noor Abad, Khoumeh Zar, Ghaemieh and Komarj (Figure 1) and plain is covered by quaternary alluvial. Therefore, it is important to study this fault. So this fault needs a closer look at the various geophysical methods and in this research random method of finite fault simulation method and geomagnetic (analytical signal method) were studied.
2. Random Finite Fault Simulation
Every accelerogram is the result of the convolution of the source function, distribution function and site effect:
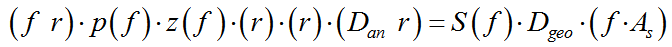
where, S(f) is the source function, Dgeo(r) is the geometrical attenuation coefficient, Dan(f,r) is the path attenuation coefficient, P(f) is the upper shell coefficient, and Z(f) is the site effect. Motazedian and Atkinson (2005) proposed the extended fault simulation (EXSIM) application for simulation of near-fault accelerations with positive pulse effects. In this method, the fault plane is divided into N micro-faults using the random finite fault modeling method based on dynamic corner frequency. Each micro-fault is then used as a small point source [4] . The ground motions caused by these micro-faults are summed based on temporal delays to obtain the time his-
![]()
![]()
Figure 1. Location and geological map of the study area.
tory of the target earthquake. The acceleration spectrum for the i-th micro-fault (ij) is expressed as follows (Relation 2):
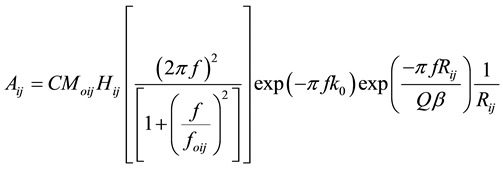
where, Moij and foij denotes the seismic moment and dynamic corner frequency of the ij-th micro-fault, respectively. Moreover, foij is a function of stress decline, Rij is the distance between the ij-th micro-fault and the observation point, and β shows the shear wave velocity [5] . The term 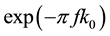 is a low-pass filter aimed for modeling the effect of the near-surface spectrum loss parameter (k). The latter parameter is usually demonstrated by rapid spectrum loss at higher frequencies [6] . The term 1/R shows the geometrical attenuation caused by body waves while C is the scale coefficient and Hij is a function of corner frequency.
is a low-pass filter aimed for modeling the effect of the near-surface spectrum loss parameter (k). The latter parameter is usually demonstrated by rapid spectrum loss at higher frequencies [6] . The term 1/R shows the geometrical attenuation caused by body waves while C is the scale coefficient and Hij is a function of corner frequency.
3. Research Method
In this study, accelerograms were obtained using SeismoSignal and the baseline correction method [7] . The processing of these accelerograms involved the use of band-pass Butterworth digital filter with cut-off frequencies of 25.0 and 0.2 Hz. The filter was used to remove low- and high-frequency noises. In order to determine the shear wave window, the starting point of the wave (S) was marked through observation on the accelerogram and the end of the window was marked using the Kinoshita algorithm (1994) [8] . The spectrum loss parameter (k) and the frequency dependence of shear wave quality factor (Qs) are among the input parameters for the random finite fault simulation method. The values of k and the frequency dependence of shear wave quality factor for the Kazeron region were assumed to be 1.14 and Q = 128, respectively [9] . Since no information was available about the slip and heterogeneity of the fault causing the September 7, 2010 Kazeron Earthquake, EXSIM was used to determine random slip values based on normal distributions. Environmental density and shear wave velocity, which are used to describe the propagation medium, were assumed to be 2.8 g/cm3 and 3.2 km/s, respectively [10] . Another important parameter was stress decline. Since the stress decline parameter governs the higher frequencies of Fourier spectrum, trial and error calculations were conducted to obtain an optimal value of 60 bar, which gave the highest level of compliance between the observational and actual Fourier spectra. Fault dimensions were calculated using Wells and Coppersmith (1994) relations [11] . According to these relations, the fault length along the strike direction was 10 km and the fault width along the dip direction was 7 km. Based on the distribution of aftershocks and the existing self-similarity, the fault plane was divided into 10 elements along its length and 7 elements along its width. Since the coordinates of the hypocenter was (i, j) = (0, 0), the coordinates for the epicenter was obtained to be 29.88N - 51.57E. Figure 2 shows the reported location of the epicenter on the Dem map of the region. The source of the failure of micro faults was randomly assumed to be (i, j) =
![]()
Figure 2. Epicenter of December 20, 2010 Regan Earthquake (BHRC) along with the name of stations recording the earth- quake.
(0, 0) which leads to a radial propagation. In this study, records of the fault causing the September 27, 2010 Kazeron Earthquake were studied and the optimal strike and dip values were estimated to be 27 and 50 degrees, respectively. Table 1 shows the results of this study along with other findings reported by other researchers. Ac- cording to results of comparison of the actual and simulated accelerograms, the strike and dip values in this study are highly compatible with actual values. Seemingly, the fault strike (Qatar-Kazeron fault) was the cause of the September 27, 2010 Kazeron Earthquake.
Figure 3 shows the results of the comparison between the time history of horizontal components of Kazeron earthquake and the accelerograms simulated in Kazeron and Qaemieh stations. Simulation results are adequately similar to actual accelerograms. In order to determine the site reinforcement coefficient a site with an area of over 30 m and shear wave velocity of 520 m/s were used [12] [13] . Figure 4 shows the results of the comparison between the Fourier spectra of the horizontal components acceleration and accelerograms simulated in Kazeron and Qaemieh stations. Figure 5 also shows the comparison between the components of Kazeron earth-
![]()
Table 1. Comparison of the results of this research and parameters reported for the fault causing the Kazeron earthquake by other researchers.
![]()
Figure 3. Time history of horizontal components accelerations recorded in Kazeron and Qaemieh stations along with si- mulated accelerograms.
![]()
Figure 4. Comparison of Fourier spectra for horizontal component accelerations and simulated accelerations in Kazero and Qaemieh stations.
![]()
Figure 5. Comparison of components of speedograms recorded in Kazeron and Qaemieh stations.
quake speedogram and simulated speedograms.
4. Analytical Signal Mapping
Satellite magnetic data was used in the resolution-based magnetic remote sensing studies. Image processing and filtering plays an important role in the interpretation of magnetic data. In the interpretation of magnetic remote sensing data, removal of regional effects and local anomalies associated with subsurface shallow constructions increases the resolution of deep structures.
Analytical signal is a quantitative method for interpretation of potential field data. According to the studies, magnetic body and magnetization direction do not influence the analytical signal. Use of analytical signals for measuring the depth of the magnetic body reduces the complexity of calculations and the interference effect. The analytical signal filter removes first-grade regional effects in three directions through differentiation and adds to the clarity of the magnetic body by removing the effect of surface anomalies (noises). Two-dimensional analytic fluctuations are of importance in the processing of magnetic field data. This provides for obtaining a signal independent of the magnetized source. This method is based on the removal of noises using derivatives in different directions. In this method, derivatives are obtained in different directions first-grade regional effects are removed in three directions while the effect of surface anomalies not related to the deposit is also omitted more optimally. The potential field shown by the magnetometer is composed of magnetic body and magnetic field strength in the region. The aforementioned two parameters can be separated. The Euler-Werner torsion relation can be used to express this phenomenon in mathematical terms. The analytic signal method can be used to determine anomaly edges as well as the maximum and minimum depths of anomalies. The analytical signal for gravity gradients is expressed as follows:
 (2)
(2)
The amplitude of the analytical signal is also obtained as follows:
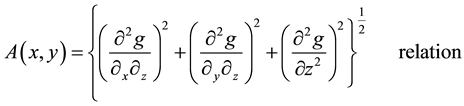 (3)
(3)
In order to determine the horizontal position of edges the precise location of the maximum value of the analytical signal is required. The maximum value or maximum amplitude of the analytical signal completely lies on anomaly edges. The analytical signal function is useful for interpretation of magnetic data. Analytical signals can be also used for determining the contact surface depth. Analytical signal is also useful for determining the location and depth of magnetic sources. The amplitude of an analytical signal reaches its maximum level on the body or edges of the source depending on the source type. Considering different location windows it is possible to obtain the maximum analytical signal amplitude in each direction. By connecting the maximum points on each window the boundary of the anomaly are obtained. Depth can be estimated using windows for the points lying on the boundary.
As seen in the analytical signal map (Figure 6), there are some magnetic discontinuities that started with a north-west strike followed by a northwest-southeast strike. This trend is consistent with the Kazeron fault trend but is several kilometers away from it.
According to the results of geomagnetic studies and satellite surveys the best filter for defining the fault at depths is the analytical signal filter. The surface of the fault determined using the remote sensing method complied with the Kazeron fault and lied along the north-south strike direction (northeast-southwest) parallel to the fault.
The resulting epicenter coordinates (28.88N - 51.57E) is highly compliant with the epicenter reported by BHRC. The resulting focal depth (app. 8 km) is also highly compliant with the focal depth reported by IGTU. Accor- dingly the closest distance between the two faults was estimated to be 5.6 km that it is clear in Figure 7.
According to the results of random finite fault method, the fault location complied with the location on the geological map demonstrating a depth of 8 km (surface) and a dip of 50 degrees. Although these results are contradictory, information obtained using the geomagnetic investigation suggest that the fault is located 5 to 8 km
![]()
Figure 6. The location of the extracted seismograms and faults on the ana- lytical signal map.
![]()
Figure 7. The closest distance between the two faults was estimated to be 5.6 km.
![]()
Figure 8. Combination of research results (geomagnetic, accelerograms and remote sensing) and calculation methods.
away from its surface toward the east. According to the results of these two methods (geophysical method and accelerograms), from the fault surface to a depth of 8 km the fault has an almost vertical dip towards east and then develops into a listric fault with a dip of 50 degrees to a depth of 12 km. Accordingly combination of research results shown in Figure 8.
5. Conclusions
According to the results of geomagnetic studies and satellite surveys, the best filter for determining faults at depths is the analytical signal filter.
The fault surface obtained using the remote sensing method demonstrated a trend similar to that of Kazeron fault and lied parallel to the fault along the northwest direction.
The epicenter obtained from these investigations (28.88N - 51.57E) was properly complaint with the epicenter reported by BHRC. The resulting focal depth (app. 8 km) was also highly compliant with the focal depth re- ported by IGTU.
The starting point for the microfault failure was randomly assumed to be (i, j) = (0, 0) which results in radial propagation.
The strike and dip of the fault planes were estimated to be 27 and 50 degrees, respectively. These values are consistent with the values reported by HRVD. Seemingly, the Kazeron fault dip was the cause of the September 27, 2010 Kazeron earthquake. This finding also complies with the preliminary report of the meteorological orga- nization.
The Fourier spectra for the simulated and observed amplitudes provided by stations located less than 80 km from the epicenter (Qaemieh, Quyem, Kenartakhte, Kazeron, and Khan Zeynan stations) demonstrated a good correlation between the amplitude and wave shape in the 0.5 - 20.0 Hz frequency interval. This indicates that the fault parameters used as inputs for random finite fault simulation of strong ground motion were suitable.
Based on the results of geomagnetic studies, accelerograms and the random finite fault method, the resulting fault location complies with the location on the geological map. It has a depth of 8 km and a dip of 50 degrees. Although these results are contradictory, information obtained using the geomagnetic investigation suggest that the fault is located 5 to 8 km away from its surface towards the east. According to the results of these two methods, from the fault surface to a depth of 8 km the fault has an almost vertical dip towards east and then it develops into a listric fault with a dip of 50 degrees to a depth of 12 km.