The Role of a Novel Discrete-Time MRAC Based Motion Cueing on Loss of Control at a Hexapod Driving Simulator ()
1. Introduction
Multi-sensory datafusion: such as visual, auditory, haptic, inertial, vestibular, neuromuscular signals are of importance to represent a proper sensation (objectively) and so a perception (subjectively as cognition) in motion base driving simulators [1] -[10] .
A use study of the physiological measurements (biofeedback methods) has been presented to estimate user interruptibility status by [3] . Heart Rate Variability (HRV) and Electromyogram (EMG) signals have been registered as users performed a diversity of assignments. Results have elicited high correlations for both HRV and EMG (r = 0.96 and r = 0.85 respectively) with user subjective reports for interruptibility [3] .
Motion sickness has been discussed when a moving visual surround induces the illusion of self-rotation in [4] [11] . The vestibulo-ocular reflex and the occurrence of motion sickness are attached to the gravito-inertial force level according to [12] .
Motion cueing for a 2 DOF (degrees of freedom) driving simulator has been examined by [6] . The theme of that research has been to test and compare performances of different washout algorithms applied to such sort of platform. The results have depicted that there has been no significant difference among those approaches [6] . The effects of different washout algorithms used for Stewart platforms (6 DOF) on subjective and objective ratings have been discussed in [2] . According to the simulator sickness test, closed-loop motion cueing algorithm; the subjects have reacted less stressfully (cold sweat) to the conditions, whereas they have behaved more stressfully in the conditions of the open-loop motion cueing (classical) algorithm. Regarding the visual sickness of the participants, closed-loop motion cueing algorithm has presented the most reasonable situation. Also concerning the mental pressure, the statistical distribution points out an agreeable experience for closed-loop motion cueing algorithm comparing to the open-loop motion cueing algorithm. Based upon the “modified simulator sickness questionnaire”, the most realistic acceleration has been perceived by operating the motion platform with closed- loop motion cueing algorithm; where the most unpleasant steering has been coincided by exploiting the motion platform by open-loop motion cueing algorithm; and whereas the most agreeable condition has been experienced at closed-loop motion cueing algorithm with regards to perception of the pitch motion severity. Furthermore, the perception on curvature has been assessed as the most disagreeably during the attempts with classical washout algorithms [2] .
Restituting the inertial cues on driving simulators play an important role to sustain a more proper functioning in proximity to the reality [13] [14] . Simulator sickness deals with whether this convergence is obtained or not, as being one of the main research issues for the driving simulators. Simulator sickness was assessed between moving base and fixed base simulators by [15] . However, there has been a very few publications of vehicle (visual)-vestibular cue conflict based approach and its correlation with the neuromuscular dynamics. This paper addresses a methodology in order to rate the loss of adhesion (LOA) as well as the agility and alertness level of the drivers as a correlated function of the vestibular cues with the EMGRMS total power. Due to the restricted workspace, it is not possible to represent the vehicle dynamics permanently with scale one to one on the motion platform [6] [12] [16] - [18] .
This research work was performed under the dynamic operations of the SAAM driving simulator as with a classical and a MRAC controlled tracking of the hexapod platform. The dynamic simulators’ utilization scope diversifies from driver training to research purposes such as vehicle dynamics control, advanced driver assistance systems (ADAS) [19] [20] . The dynamic driving simulator SAAM (Simulateur Automobile Arts et Métiers) is made up of a hexapod platform system. It is exploited on a RENAULT Twin go 2 cabin with the original control instruments (gas, brake pedals, steering wheel). The visual system is handled by a 150˚ dome view. Multi-level real-time measuring techniques (XSens motion tracker, Biopac EMG (electromyography) device, Technoconcept postural stability platform) [1] are available, which are already used with numerous experiments/scenarios such as sinus steer test, NATO chicane, etc. The vehicle accelerations of translations (longitudinal X, lateral Y and vertical Z axes) as well as the vehicle accelerations of roll and pitch, which correspond to the vehicle dynamics, are taken into account for the control. Then the platform positions, velocities and accelerations were controlled and fed back to minimize the conflict between the vehicle and the platform levels [2] . The paper is organized as: Section 2 explains the proposed control approach for the dynamic platform of the driving simulator. Section 3 describes the used materials and methodology in order to analyze the multiple level data acquisition (neuromuscular via using EMG, vestibular through using motion tracking sensor and vehicle levels via SCANeR studio software). Section 4 discusses the results. And finally, Section 5 concludes up the paper.
2. Proposed Control Approach
This paper explores a comparative study between an open and a closed loop controlled platform to maintain the vehicle pursuing a chicane maneuver scenario (loss of control-LOC). For the evaluation and the validation procedure [3] [16] [18] [21] - [24] , the scenario driven on the simulator SAAM with a classical motion cueing (open loop control) and a MRAC motion cueing (closed loop control) to describe the impact of the feedback control on LOC. The results from a case study were illustrated in the scope of this research with real time controls of the platform at a longitudinal velocity of 60 km/h. This research surveys the following hypotheses:
-Neuromuscular (EMGRMS total power) and vehicle dynamics (lateral displacement of the vehicle CG (center of gravity)) interaction indicates the limit of LOC in the driving simulation experiments.
If they are positively significant correlated, it means that an avoidance loss of control (LOC) is possible to occur.
If they are negatively significantly correlated, it shows that the drivers are prone to experience a loss of control (LOC) phenomenon.
-Vehicle dynamics approach (lateral displacement of the vehicle CG): Lateral displacement area decreases when the MRAC algorithm is used (avoidance of LOC).
-Vestibular (roll velocity perception threshold―RVT) and neuromuscular dynamics (EMGRMS mean total power and EMGRMS maximum total power) interaction gives the characteristics of the driver: If they are positively correlated; perception of agility, in other words alertness level of the drivers and avoidance of LOC increase when the MRAC motion cueing is used.
2.1. Motion Cueing Algorithm
The proposed classical motion cueing algorithm’s sketch is indicated with continuous lines and arrows where the model reference controlled motion cueing algorithm’s sketch was drawn with discrete lines and arrows (Figure 1).
The proposed MRAC motion cueing algorithm here uses the same filters, gains (Figure 1 and Table 1) like used in the classical algorithm to compare the effects of the model reference adaptive control of the dynamic driving simulator. The main idea for Model Reference Adaptive Control (MRAC, which is also known as an
![]()
Figure 1. Classical and MRAC motion cueing algorithms sketches.
![]()
Table 1. Classical motion cueing algorithm parameters [25] .
MRAS or Model Reference Adaptive System) is to build a closed-loop controller with parameters that can be updated to change the response of the system. The output of the system is compared to a desired response from a reference model. The control parameters are updated based on this error. The goal is for the parameters to converge to ideal values that cause the plant response to match the response of the reference model. It can focus on the continuous-time case and also on discrete-time design. A discrete-time MRAC was referred in this paper. The objective is to regulate the output minimized (platform-vehicle levels’ sensed acceleration difference minimization). The system (dynamic driving simulator) is subject to disturbances and is driven by controls [26] - [30] .
Table 2 illustrates the constraints of the dynamic driving simulator SAAM, which was used in the real-time dll plugin in the SCANeR studio software for the both motion cueing algorithms. For the longitudinal, lateral and vertical displacements, the used gains were 0.2, 0.2 and 0.22 respectively.
The design step searches a state-feedback law that minimizes the cost function via applying this logic. Figure 2 illustrates the research method for the whole group of the subjects used in this article.
Both of the motion control algorithms (classical and MRAC) were integrated at the dynamic driving simulator SAAM with a “dll plugin” which were created with Microsoft Visual 2008 C++ used in SCANeR studio version 1.1.
2.2. Control Problem
We considered adiscrete-time MIMO (multiple-input multiple-output) system described by [27] - [30]
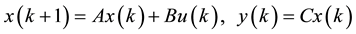 (1)
(1)
with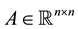 ,
, 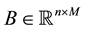 and
and 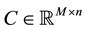 being unknown and constant parameter matrices and
being unknown and constant parameter matrices and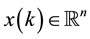 ,
, 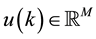 and
and 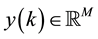 being the system state, input and output vector signals.
being the system state, input and output vector signals.
2.2.1. Control Objective
The control objective is to design a state feedback control signal u(k) in Equation (1) such that all the closed- loop signals remain bounded and the system output signal y(k) tracks a given reference output 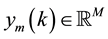 that is generated from the reference model system
that is generated from the reference model system
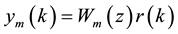 (2)
(2)
Wm(z) is an M ´ M transfer matrix, and r(k), an M-dimensional real array, is a bounded reference input signal [27] [30] [31] .
2.2.2. Assumptions
To begin the real-time controller design which is implemented in driving simulator as “dll plugin”, we assume [27] :
(A1) All zeros of  lie within the unit circle in the z-plane;
lie within the unit circle in the z-plane;
(A2)  have full rank, there is a left interactor matrix ξm(z) for all
have full rank, there is a left interactor matrix ξm(z) for all 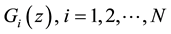
![]()
Figure 2. Hypotheses: Our hypotheses are made up of three parts. 1) We stated that if the lateral displacement of the vehicle CG used inside the driving simulator and the power spent by arm muscles (from flexor carpi radialis) are positively correlated, it is an indicator of avoidance of LOA (LOC). Inversely, if they are negatively correlated, it is an objective metrics of occurrence of LOA. 2) We also declared that if the lateral displacement of the vehicle CG increases LOA occurs and in adverse case LOA decreases. 3) According to our third hypothesis, if the head (vestibular) level roll velocity perception threshold and the arm muscles power dissipation are positively correlated (cues conflict decrease) the alertness/agility level of the drivers increase too. We checked this criterion with respect to the real-time mean and maximum values of the total EMGRMS power measured from the arm muscles. Mean EMGRMS power is corresponding to the whole scenario whereas the maximum value of the EMGRMS power is referring to the sudden change mostly depending on the sudden change of the road curvatures, i.e. LOA.
![]()
Table 2. Limits of each degree of freedom (DOF) for the SAAM driving simulator [25] .
and the reference system transfer matrix![]() ;
;
(A3) All leading minors ![]() of the high frequency gain matrix Kp are nonzero and their signs are known.
of the high frequency gain matrix Kp are nonzero and their signs are known.
2.2.3. State Feedback for State Tracking
For a state feedback for state tracking design, the controller structure is
![]() (3)
(3)
where ![]() and
and ![]() are parameter matrices updated from some adaptive laws, so that
are parameter matrices updated from some adaptive laws, so that
the plant state vector signal x(k) can asymptotically track a reference state vector signal xm(k) generated from a chosen reference system
![]() (4)
(4)
where ![]() is stable and
is stable and![]() . For such an adaptive control design, the matching conditions K1(k) and K2(k) are the estimates of the nominal
. For such an adaptive control design, the matching conditions K1(k) and K2(k) are the estimates of the nominal ![]() and
and ![]() which satisfy the conditions of matching
which satisfy the conditions of matching
![]() (5)
(5)
where ![]() is the high frequency gain matrix of
is the high frequency gain matrix of![]() . The existence of
. The existence of ![]() and
and ![]() is guaranteed under the nominal system condition: (A4) (A, B) is stabilizable and (A, C) is observable.
is guaranteed under the nominal system condition: (A4) (A, B) is stabilizable and (A, C) is observable.
2.2.4. Tracking Error Equation
Substituting the control law Equation (3) in Equation (1), we obtain
![]() (6)
(6)
In view of the reference model Equation (2), matching equations Equation (5) and Equation (6), the output tracking error ![]() is
is
![]() (7)
(7)
where ![]() converges to zero exponentially and
converges to zero exponentially and
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
2.2.5. LDS Decomposition
In this section, we present the design and analysis of an adaptive scheme based on the LDS decomposition of the high frequency gain matrix KP.
To design an adaptive parameter update law, it is crucial to develop an error model in terms of some related parameter errors and the tracking error![]() .
.
2.2.6. Error Model
Neglecting the term![]() , we obtain from Equation (7) and Equation (2)
, we obtain from Equation (7) and Equation (2)
![]() (12)
(12)
To deal with the uncertainty of the high frequency gainmatrix KP, we use its LDS decomposition
![]() (13)
(13)
where ![]() with
with![]() , Ls is an M ´ M unit triangular matrix, and
, Ls is an M ´ M unit triangular matrix, and
![]() (14)
(14)
such that![]() , where
, where ![]() is called adaptive gain, and
is called adaptive gain, and ![]() is the second term in the diagonal of the matrix Ds of the LDS decomposition [27] [28] , substituting Equation (13) in Equation (12) yields
is the second term in the diagonal of the matrix Ds of the LDS decomposition [27] [28] , substituting Equation (13) in Equation (12) yields
![]() (15)
(15)
To parameterize the unknown Ls, ![]() is introduced in Equation (16)
is introduced in Equation (16)
![]() (16)
(16)
Then, it yields (17):
![]() (17)
(17)
A filter was designed![]() , where f(z) is a stable monic polynomial of degree equals to the degree of ξm(z), operating both sides of Equation (17) by h(z)IM leads to
, where f(z) is a stable monic polynomial of degree equals to the degree of ξm(z), operating both sides of Equation (17) by h(z)IM leads to
![]() (18)
(18)
where
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Based on this parameterized error equation, we reach the estimation error signal
![]() (22)
(22)
where ![]() are the estimates of
are the estimates of![]() , and
, and ![]() are related parameter errors.
are related parameter errors.
2.2.7. Adaptive Laws
Within the estimation error model Equation (22), the chosen adaptive laws [27] :
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
where the signal ![]() is computed from Equation (22),
is computed from Equation (22), ![]() and
and ![]() are adaptation gain matrices and
are adaptation gain matrices and
![]() (27)
(27)
is a standard normalization signal, where ![]() [27] .
[27] .
3. Methods
We consider the dynamic model of the hexapod simulator described by Equation (28) which is a three state variable (x). The control inputs are (u) the pitch angle (θv), the roll angle (ϕv) and the yaw angle (ψv) of the vehicle model. Our MRAC model was given in Equation (29) (HP: high pass filtered motion, LP: low pass filtered motion) which was with a sampling interval of T = 1/60 seconds to obtain the discrete-time motion cueing algorithms implemented in our dll plugin.
![]() (28)
(28)
![]()
![]() (29)
(29)
3.1. Subjects
Twenty-six healthy participants took place in the experiments (4 females, 22 males) with a mean age of 28.9 ± 5.8 years old and a driving license holding with a mean experience of 9.7 ± 6.6 years.
3.2. Protocol
Figure 3 shows the trajectory of the chicane maneuver that we used in this experiment protocol (Here W = 1 m and L = 1.5 m). The vehicle velocity during the simulator experiments was chosen as constant at 60 km/h. The same scenario was driven at the classical and the MRAC motion cueing algorithms in order to compare the biomechanical interactions (head level dynamics and vehicle level dynamics interaction, neuromuscular dynamics and vehicle level dynamics and lastly head level dynamics and neuromuscular dynamics) of the participants.
Vestibular level dynamics of the participants refer to the head movements of them (see Figure 4). It was measured via a XSens motion tracking sensor. Vehicle level dynamics indicate the visual cues which come from the surroundings of the vehicle when it is driven at the simulator as real-time.
![]()
Figure 3. Tested trajectory of a chicane maneuver.
![]()
Figure 4. Head movement and EMG analysis.
3.3. Data Analysis
Multi-level data acquisition was performed at two levels as follows:
3.3.1. Vestibular Level Data Acquisition (through Sensor)
Such as the roll, pitch, yaw angles and rates as well as the accelerations in X,Y and Z. Quaternions have been used, since they are simpler to compose and to avoid singularity for angular calculations, so-called the problem of gimbal lock compared to Euler angles. The application domains of quaternions can be counted as computer graphics, computer vision, robotics, navigation, flight dynamics [32] and orbital mechanics of satellites [33] . Because we have dealt with the hexapod driving simulator in real-time, we have used quaternions. The data are calibrated due to three dimensional quaternion orientation.The sampling rate for the data registration during the sensor measurements is 20 Hz. For the calibrated data acquisition, the alignment reset has been chosen which simply combines the object and the heading resets at a single instant in time. This has the advantage that all co? ordinate systems can be aligned with a single action.
3.3.2. Electromyography (via Biopac System)
Electromyography (EMG) is an evaluation method of the electrical activity produced by musculoskeletal system. EMG is performed using an instrument called an electromyograph, to realize a record called an electromyogram. An electromyography detects the electrical potential generated by muscle cells [34] when these cells are electrically or neurologically activated. The signals can be analyzed to detect and identify medical abnormalities, muscle activation level, and recruitment order or to analyze the biomechanics of human or animal movements [34] .
By using the Biopac systems, several frequency and time domain techniques could be used for data reduction of EMG signals [21] .
For this study, it was chosen to deal with the EMGRMS (root mean square: which is a product of longitudinal, lateral and vertical dynamics related dissipated power) power analysis (V2/Hz in unit) in time domain, in order to investigate their associations with RVT (˚/s in unit, which is an indicator of the conflict in dynamics).
- EMGRMS mean total power yields the average power of the power spectrum within the epoch [21] .
- EMGRMS total power is equal to the sum of power at all frequencies of the power spectrum within the epoch [21] .
- Epoch corresponds to how many time steps (∆t) a whole time series signal is divided into [21] .
For the calibration of the electromyography, a gain of 1000 was used. And the Figure 4 depicts the data acquisition during the experiments; the electrical activities of the muscles were registered by a non-invasive surface EMG method through two analog channels. The signals were collected with 10 Hz for low cut-off, 500 Hz for high cut-off frequencies (a band-pass filter with a frequency range: 10 - 500 Hz).
Electrodes in black circle were connected to flexor carpi radialis muscle where the electrodes in red circle were connected to brachioradialis muscles. We measured and saved the electrical activity changes on the brachioradialis and flexor carpi radialis muscles. In this paper, we explained the results which were taken from the muscle ‘flexor carpi radialis’ (at right hand side, Figure 4).
4. Results and Discussion
4.1. Vestibular and Neuromuscular Dynamics Interaction with Vehicle Dynamics
Figure 5 corresponds to the vehicle velocity during the experiments with driver for the EMG-RV analysis done in Figure 6.
![]()
Figure 6. EMGRMS total power (mV2/Hz) and vestibular roll velocity (˚/s).
Figure 6 indicates a real-time measurement of EMGRMS total power-head roll velocity for one out of the twenty six subjects who participated in the experiments.
If Figure 3, Figure 5 and Figure 6 are evaluated together it is possible to characterize the neuromuscular dynamics (via EMG analysis), vestibular dynamics more clearly.
It can be seen that the discrepancy has been decreased between the EMGRMS total power and the roll velocity at vestibular level by using MRAC motion cueing (see Figure 6). This figure also proves less contradicting cues from the arm muscular and the vestibular dynamics system, in other words less LOA (loss of adhesion) of the vehicle or more agility and alertness levels of the driver in the lateral dynamics.
Table 3 summarizes the correlation of the arm muscle (flexor carpi radialis) power and the head level roll velocity from a sensor attached to the right ear of the drivers via a headphone (Figure 4) with the vehicle CG (center of gravity) lateral displacement for the classical motion cueing algorithm situation. From Table 3, it is seen that there have been significant correlation between vestibular roll velocity and vehicle CG lateral displacement except for Subject 1 and Subject 13. Furthermore, merely the subject 6 has yielded a positive correlation between the vestibular level roll velocity and the arm muscles power. Apart from subject 6, they have demonstrated a negative correlation, which actually represents an increased level of the visuo-vestibular cue conflict.
According to Table 3, it can be concluded that there have been significant correlations between arm muscle powers and vehicle CG lateral displacements for all the thirteen subjects at the classical motion cueing case. Moreover, a negative correlation has been resulted between the arm muscles power and the vehicle CG lateral displacements for the subjects 1, 3, 7, 8 and 13 for the classical algorithm, whereas a positive correlation has been obtained for the rest of the subjects. These correlations show us that for the 8 subjects the vehicle has been driven with the less controlloss out of the 13 subjects.
Table 4 gives the correlation of the arm muscle (flexor carpi radialis) power and the head level roll velocity with the vehicle CG (center of gravity) lateral displacement for the MRAC motion cueing algorithm case. From Table 4, it can be seen that there have been significant correlation between vestibular roll velocity and vehicle CG lateral displacement except for Subject 8. Furthermore, the subject 3, 6 and 8 have yielded a positive correlation between the vestibular level roll velocity and the arm muscles power. Apart from these subjects, they have demonstrated a negative correlation.
![]()
Table 3. Vestibular-arm muscle dynamics interaction for classical motion cueing.
*Means one zero after the point “.”, **means two zeros after the point “.”, ***means three and more than three zeros after the point “.”.
![]()
Table 4. Vestibular-arm muscle dynamics interaction for MRAC motion cueing.
*Means one zero after the point “.”, **means two zeros after the point “.”, ***means three and more than three zeros after the point “.”.
According to Table 4, it can be concluded that there have been significant correlations between arm muscle powers and vehicle CG lateral displacements apart from the subjects 3, 9 and 11 at the MRAC motion cueing condition. Moreover, a negative correlation has been coincided between the arm muscles power and the vehicle CG lateral displacements only for the subject4 for the MRAC algorithm, whereas a positive correlation has been occurred for the rest of the subjects. These correlations show us that only for the 1subject (subject 4) the vehicle has been driven with a propensity of control loss out of the 13 subjects, when uniquely the correlation between the arm muscles power and the vestibular level roll velocity are taken into account.
From Table 3, Table 4 and Figure 7, it is seen that loss of adhesion (LOA) of the vehicle causes a visuo- vestibular cues conflict (if the correlation of vestibular roll velocity with vehicle CG lateral displacement is negative) however visuo-vestibular conflict is not always followed by a LOA (if the correlation of EMGRMS total power with vehicle CG lateral displacement is negative).
Figure 8 summarizes our findings about the relationships of multi sensory (vestibular, neuromuscular, vehicle (visual)) cues with motion sickness incidence as a metrics for lateral dynamics in terms of sensory cue conflict theory [35] [36] depending on Table 3 and Table 4 respectively for this study. According to this figure; when there is no conflict at all in cues, no motion sickness is occurred. As there is visuo-vestibular cue conflict, it results as a moderate level of motion sickness. Eventually when LOA is observed, the motionsickness gets higher levels.
Table 5 illustrates the lateral displacement area (Equation (30) in m・s) [19] [20] [37] (see Figure 9) under the vehicle CG lateral displacement (YCG) from the time series graphs where t is time
![]() (30)
(30)
According to Table 5, it can be summed up that apart from the subjects 6, 7, 8 and 9 the loss of adhesion has decreased; in other words agility or alertness level of the drivers have increased for the classical algorithm comparing to MRAC algorithm which make the vehicle maintain on the desired route. In contrast for the rest of the subjects, the agility level of the drivers has increased, in other words LOC of the vehicle has decreased with MRAC motion cueing. For the subjects 6, 7, 8 and 9 (4 subjects out of 13 subjects) the classical motion cueing algorithm had the higher level of loss of control (LOC) of the vehicle in the dynamic driving simulator. For the
![]()
Figure 7. Vestibular-neuromuscular-vehicle dynamics interaction.
![]()
Figure 8. Relationships of multi sensory cues conflict with motion sickness.
rest of the subjects (9 subjects out of 13 subjects), the MRAC motion cueing algorithm brought a more controllable vehicle in the dynamic simulator as operated in real-time. This shows that the MRAC motion cueing algorithm (closed loop control) provides a less LOA and LOC comparing to the classical motion cueing algorithm (open loop control).
![]()
Table 5. Lateral displacement area for both algorithms.
4.2. Vestibular and Neuromuscular Dynamics Interaction
After having completed the data evaluation by individual as above, the overall data analysis has been studied for the thirteen subject group for each motion cueing (both for the classical and the MRAC motion cueing algorithms).
The overall data analysis was done by using a two-way ANOVA (Analysis of Variance) and Pearson’s correlation with an α = 0.05. In order to accomplish the statistical analysis, we took
- the vestibular roll velocity into account, which were measured from the right ear level of the participants during the real-time simulator experiments through the motion tracking sensor.
- the EMGRMS total power from the muscle ‘flexor carpi radialis’.
The two-way ANOVA was applied to identify the level of significance as between subjects’ principle test. The Pearson’s correlation was computed to clarify the correlation of the vestibular level roll velocity threshold with the EMGRMS power dissipation of the arm muscles.
4.2.1. Two-Way ANOVA
The two-way ANOVA tests were used to check the influence of one type of response dynamics (spent power from the arms) of the drivers on the other type of response dynamics (vestibular roll velocity) of them as an interaction metrics.
By studying the output of the two-way ANOVA for the proposed classical motion cueing algorithm, we see that there is no evidence of a significant interaction effect (F = 3.74, p = 0.085 > 0.05) between those two types of response dynamics of the drivers. We therefore can conclude that no interaction was obtained between the EMGRMS mean power and the vestibular roll velocity threshold. The test for the main effect of the vestibular roll velocity perception threshold (F = 45.17, p < 0.0001) shows a significant roll velocity perception threshold effect on the EMGRMS maximum power level. Finally, the test for the main effect of the EMGRMS mean power (F = 1360.89, p < 10−9) tells us there is an evidence to conclude that the EMGRMS mean power has a significant effect on the EMGRMS maximum power level.
By investigating the output of the two-way ANOVA for the proposed model reference adaptive control motion cueing algorithm, we see that there is no evidence of a significant interaction effect (F = 0.43, p = 0.528 > 0.05) between those two types of response dynamics of the drivers. We therefore cannot conclude that an interactionis found between the EMGRMS mean power and the roll velocity threshold. The test for the main effect of the vestibular roll velocity perception threshold (F = 9.22, p = 0.01412 < 0.05) shows a significant roll velocity perception threshold effect on the EMGRMS maximum power level. Finally, the test for the main effect of the EMGRMS mean power (F = 232.44, p < 10−6) tells us there is an evidence to conclude that the EMGRMS mean power has a significant effect on the EMGRMS maximum power level.
4.2.2. Pearson’s Correlation
Having searched the relationships of the roll velocity thresholds with the EMGRMS mean and maximum total power, we recognized that if we drive the same scenario with the MRAC, it shows a more alerted (agile) mode compared to the classical motion cueing algorithm. Because, the correlation coefficients (r) between the roll velocity thresholds and the EMGRMS mean/maximum total power are positive for the MRAC and negative for the classical motion cueing algorithm.
We described the RV (roll velocity) at “vestibular” level [5] [6] [19] [20] . MATLAB/Simulink applications were used to process the RVT data (maximum head level roll velocity at low frequent motion independent from the direction): Vestibular level roll velocity signals were conditioned with a 1st order Butterworth low-pass filter at 5 Hz.
Root-mean square (RMS) of EMG (EMGRMS) (mV) values were computed based on a total range of motion during the driving phase of the simulator experiments [18] [29] , using the following Equation (31):
![]() (31)
(31)
where t is the onset of signal time and Tis the duration of RMS averaging [38] .
For the frequency domain analysis used in this study to determine the spent power/energy by the arm muscles of the drivers, a Fast Fourier Transformation algorithm was used to calculate the power spectrum of EMG signals (mV) [34] [38] with the following Equation (32):
![]() (32)
(32)
where xn is a set of consecutive EMG signals with the specific number of epochs, PSD is power spectral density in mV2/Hz [34] [38] .
In this article:
- EMGRMS total power indicates the dissipated power (times series data) during the driving simulation experiments (Equation (31) and Equation (32)). It yields the sum of the power at all frequencies of the power spectrum within the epoch.
- EMGRMS maximum total power refers to the peak values (one value point) obtained from the dissipated energy during the driving simulation experiments (Equation (31) and Equation (32)).
- EMGRMS mean total power indicates the mean of the sum of the dissipated power (one value point) at all frequencies during the driving simulation experiments (Equation (31) and Equation (32)).
- Roll velocity perception threshold gives maximum vestibular level roll velocityat low frequent motion independent from the direction: Those signals were conditioned with a 1st order Butterworth low-pass filter at 5 Hz.
Figure 10 and Figure 11 illustrate the difference of the both motion cueing algorithms in terms of RVT (˚/s) to EMGRMS maximum total power (mV2/Hz) as well as to EMGRMS mean total power (mV2/Hz) changes. In order to assess the relationships, we used MATLAB. The vertical axes were illustrated in the logarithmic scale in order to show the data points better.
Due to Figure 12, it is clearly seen that some of the participants reached extreme outliers (red stars) in terms of roll velocity thresholds by driving the classical motion cueing algorithms while the RVT for the MRAC motion cueing algorithm showed no extreme outliers. In addition, the discrepancy of the RVT for classical motion cueing algorithm (from −3.1˚/s to 2.4˚/s, it makes a discrepancy of 5.5˚/s) is greater than the one (from −0.8˚/s to 1.1˚/s, it makes a discrepancy of 1.9˚/s) in MRAC motion cueing algorithm, which also specifies a higher level of vestibular sensory conflict.
According to Pearson’s correlation, it is shown that the RVT and the EMGRMS mean power are positively correlated (r = 0.228, p = 0.453) for the MRAC algorithm and they are negatively correlated (r = −0.167, p = 0.586) for the classical algorithm.
According to Pearson’s correlation, it is shown that the RVT and the EMGRMS maximum power are positively
![]()
Figure 10. RVT and EMG RMS maximum total power analysis relationships for all subjects.
![]()
Figure 11. RVT and EMG RMS mean total power analysis relationships for all subjects.
![]()
Figure 12. RVT comparison for the classical and the MRAC motion cueing algorithms for all subjects.
correlated (r = 0.192, p = 0.531) for the MRAC motion cueing algorithm and they are negatively correlated (r = −0.178, p = 0.560) for the classical motion cueing algorithm. (Figure 10 and Figure 11).
5. Conclusion
Head roll velocity, arm muscle and vehicle dynamics interaction were investigated. For the classical motion cueing the discrepancy of the curves (vestibular-arm muscle dynamics) has increased (see Figure 6). Concluding up from Table 5; 9 out of the 13 subjects have obtained a lower amount of surface according to the lateral displacement of the vehicle CG with the MRAC algorithm. This indicates an improvement in LOA (loss of adhesion) at the MRAC motion cueing comparing to the classical motion cueing (69.2% of decrease in LOA, 30.8 % of increase in LOA). Due to Table 3, 5 out of 13 subjects have shown a propensity on LOA and decrease in agility/alertness level of the drivers at the classical algorithm (proximity to a LOA incidence is 38.5%). Table 4 has illuminated an inclination to an incidence of LOA for merely 1 subject (propensity to a LOA is 7.7%).
We also investigated the vestibular sensed roll velocity perception threshold (impulse effect dynamics: high frequent motion) with the total power spent by the arm muscles. It gave an idea about the driver’s behaviours as “alertness (agility)”.
Having a closed loop control of the hexapod platform (a MRAC motion cueing strategy) supplied more alertness (39.5% increase in agility: r = 0.228, p = 0.453 for the MRAC algorithm and r = −0.167, p = 0.586 for the classical algorithm in terms of RVT-EMGRMS mean total power. And also 37% increase in agility: r = 0.192, p = 0.531 for the MRAC algorithm and r = −0.178, p = 0.560 for the classical algorithm in terms of RVT-EMGRMS maximum total power), that helps the dynamic simulator be driven more controllably, compared to an open loop control of the hexapod platform (a classic motion cueing strategy) with the same filters and gains (Figure 1 and Table 1).
We thus cannot conclude that there is an interaction between the EMGRMS means power and the roll velocity threshold. The test for the main influence of the vestibular roll velocity perception threshold indicates a significant roll velocity perception threshold influence on the EMGRMS maximum power level. Eventually, the test for the main effect of the EMGRMS mean power gives us an evidence to conclude that there is a significant EMGRMS mean power effect on the EMGRMS maximum power level for both classical and MRAC motion cueing algorithms.
As a conclusion, the MRAC motion cueing strategy optimized the dynamic simulator condition with respect to the classical motion cueing strategy, so that it resulted as an improved situation for the drivers in terms of the “avoidance of LOA” and improving the “motion sickness” depending on sensory conflict theory between neuromuscular-vehicle (visual) cues, between vestibular-vehicle (visual) cues.
It also proved that the neuromuscular-vehicle dynamics conflict has influence on visuo-vestibular conflict; however, the visuo-vestibular cue conflict does not influence the neuromuscular-vehicle dynamics interactions.
As prospective work, we would like to evaluate the sickness regarding the pitch velocity/acceleration perception threshold as well as the neuromuscular-vestibular reaction time relationships of the drivers on various road scenarios, under different controls of the hexapod platform with correlations in inertial, vestibular, neuromuscular cues.
Acknowledgements
Arts et Métiers Paris Tech built up the SAAM driving simulator with the partnership of Renault.
NOTES
*Corresponding author.