Review of Non-Newtonian Mathematical Models for Rheological Characteristics of Viscoelastic Composites

Robenson Cherizol^1,2,3*, Mohini Sain^1,3, Jimi Tjong²

¹Centre for Biocomposites and Biomaterials Processing, Faculty of Forestry, University of Toronto, Toronto, Canada.
²Powertrain Engineering Research & Development Centre, Ford Motor Company, Windsor, Canada.
³Department of Chemical Engineering & Applied Chemistry, University of Toronto, Toronto, Canada.

DOI: 10.4236/gsc.2015.51002                

Abstract

This study presents an overview of viscoelastic characteristics of biocomposites derived of natural-fibre-reinforced thermoplastic polymers and predictive models have been presented in order to understand their rheological behavior. Various constitutive equations are reviewed for a better understanding of their applicability to polymer melt in determining the viscosity. The models to be investigated are the Giesekus-Leonov model, the Upper Convected Maxwell (UCM) model, the White-Metzner model, K-BKZ model, the Oldroyd-B model, and the Phan-Thien-Tanner models. The aforementioned models are the most powerful for predicting the rheological behavior of hybrid and green viscoelastic materials in the presence of high shear rate and in all dimensions. The Phan-Thien Tanner model, the Oldroyd-B model, and the Giesekus model can be used in various modes to fit the relaxation modulus accurately and to predict the shear thinning as well as shear thickening characteristics. The Phan-Thien Tanner, K-BKZ, Upper convected Maxwell, Oldroyd-B, and Giesekus models predicted the steady shear viscosity and the transient first normal stress coefficient better than the White-Metzner model for green-fibre-reinforced thermoplastic composites.

Keywords

Rheological Behavior, Mathematical Models, Viscoelastic Characteristics, Non-Newtonian Fluids, Shear Viscosity

1. Introduction

The rheological properties and extrudate behavior of polymer melts are of central importance in the processing and fabrication of polymer products. The melt-rheological behavior of short sisal, coir, and pineapple fibre-re- inforced polymer systems has been studied in various works [1] [2] . However, there is limited research on the effects of parameters such as the fibre length, the fibre-matrix interaction, and the aspect ratio of green-fibre-re- inforced thermoplastic biopolymer composites on nonlinear rheological behavior [3] [4] .

The mathematical explanation of a viscoelastic fluid is much more complex than its Newtonian counterparts. In addition to the conservation equations of mass and momentum, the constitutive equation or rheological equation of state is required; this relates stress to deformation. For a viscoelastic liquid this relationship is nonlinear and it has no standard form universally valid for each fluid in every flow situation. This reality is one of the reasons why the subject of viscoelasticity is so challenging.

The constitutive equation should not only describe the rheological characteristic of the polymer melt but also give the final fibre orientation of the composite. For this reason it is fundamental to evaluate the role of the biocomposite’s rheology and the natural fibre-polymer interaction. It has been observed that the total stress of the composite increases as fibres are added; consequently a satisfactory constitutive equation could be achieved by adding an extra stress term to an already existing constitutive equation, which then adequately describes the polymer melt [5] -[7] .

Accordingly, constitutive equations found in the literature that adequately describe polymer melt will be explored for their application in biocomposites processing. Particular focus will be given to nonlinear rheological characteristics of viscoelastic materials. The power-law, Cross WFL, Casson, Bird-Carreau and Hershel Bulkley models are among the most preferred rheological models due to their ability to predict velocity and pressure distributions in uniform flows in addition to their simple representation of shear thinning behaviour [7] - [12] . However, in the case of high shear stress of viscoelastic polymer melt, the predictive power of these models is considerably reduced [10] .

In this study, a review of nonlinear rheological models for viscoelastic materials from natural-fibre-reinforced thermoplastic polymers will be presented by a special review of the Upper convected Maxwell, Phan-Thien- Tanner (PTT), K-BKZ, Oldroyd-B, Giesekus and Whhite-Metzner constitutive models.

2. Viscoelastic Characteristics of Materials

Viscoelasticity is the property of a material to demonstrate both viscous and elastic properties under the same conditions when it undergoes deformation. Viscous materials present resistance to shear flow and strain linearly with time when a stress is applied. The shear stress of these materials depends on strain: when strain is applied and then released, they return to their initial configuration. Some common and well-known viscoelastic materials include paint, blood, ketchup, honey, mayonnaise, polymer melt, polymer solution and suspension, shampoo, and corn starch.

At constant temperature, water, air, ethanol, and benzene are represented as Newtonian fluids. This means that the rapport between the shear stress versus shear rate is a straight line with a constant slope for a fixed temperature that is independent of the shear rate. Also, the plot passes through the origin: that is, the shear rate is zero when the shear stress is zero [13] .

A fluid that does not behave in a Newtonian fashion between shear stress and shear rate when it undergoes deformation is commonly termed non-Newtonian. This means that the relation between shear stress and shear is not a straight line but is non-linear. High-molecular-weight liquids, which include polymer melts and solutions of polymers, as well as liquids in which fine particles are suspended, are usually non-Newtonian. In this case, the slope of the shear stress versus shear rate plot will not be constant as we change the shear rate. When viscosity decreases with increasing shear rate, the fluid is called shear-thinning. In the opposite case, where the viscosity increases as the fluid is subjected to a higher shear rate, the fluid is called shear-thickening. Shear-thinning fluids also are called pseudoplastic fluids and shear-thickening fluids are also called dilatants. Shear-thinning behavior is more common than shear-thickening [13] - [16] .

Another type of non-Newtonian fluid is viscoplastic or “yield stress” fluid. This is a fluid that will not flow when only a small shear stress is applied. The shear stress must exceed a critical value known as the yield stress for the fluid to start flowing. Hence, viscoplastic fluids behave like solids when the applied shear stress is less than the yield stress. Once it exceeds the yield stress, the viscoplastic fluid will flow just like an ordinary fluid [14] [15] .

On the other hand, some classes of fluids exhibit time-dependent behavior. This means that even ata given constant shear rate, the viscosity may vary with time. This category of material comprises both thixotropic and rheopectic fluids, whose behaviors in this respect are opposites. The viscosity of a thixotropic liquid will decrease with time under a constant applied shear stress. However, when the stress is removed, the viscosity will gradually recover with time as well. By contrast, rheopectic fluid behavior can be observed when the fluid increases in viscosity with time when a constant shear stress is applied [15] [16] .

3. Rheological Modelling of Viscoelastic Composites

Mathematical models of viscoelasticity are mostly based on a differential or integral representation. From a mathematical point of view, the differential representation is easier to handle than the integral one. However, the integral representation is capable of predicting the time dependence more generally.

The characteristic feature of linear viscoelastic materials is that the stress is linearly proportional to the strain history. Linear viscoelasticity is usually applicable only for small deformations, low rate, low stress, and linear materials. However, in reality about 90% of fluids are nonlinear, with large deformations, and with nonlinear response in the presence of such deformations. Nonlinear viscoelastic behavior is usually exhibited when the deformation is large and most of the time when the material changes its properties under deformations [17] - [24] . Consequently, nonlinear viscoelastic mathematical models are needed [25] -[30] .

Existing nonlinear mathematical rheological models are often constructed through modifications and extensions to higher-order stress or strain terms of the linear theory [31] . As noted earlier, from a mathematical point of view, the integral representation of a viscoelastic constitutive equation is more difficult to perform than the differential form. Thus, several models characterized by elastic, viscous, and inertial nonlinear contributions with various complexities have been developed for describing the nonlinear behavior of these materials [32] . However, in these models, due to the mathematical complications, only the elastic or viscous nonlinearity is often taken into account and the inertial contribution is ignored. Moreover, there are only a few theoretical models formulated with constant-value rheological material parameters.

For these reasons, nonlinear models with constant rheological coefficients are required. The elastic and viscous nonlinearities are taken simultaneously into consideration through a simple nonlinear generalized Maxwell fluid model consisting of a nonlinear spring connected in series with a nonlinear dashpot obeying a power law with constant material coefficients [33] -[36] . According to a previous study by Bauer (1984), suitable constitutive equations for viscoelastic materials must relate stress, strain, and their higher time derivatives: or better said, they must take into consideration the elastic, viscous, and inertial nonlinearities simultaneously [35] . Moreover, various researchers have explored how polymer viscoelasticity affects the diameter distribution of polymer melt- extrudate fibres and have demonstrated that increasing the melt viscosity leads to an increase in fibre diameter but has little effect on the diameter distribution [36] . The commonly used Phan-Thien-Tanner (PTT) and Upper- Convected Maxwell (UCM) constitutive models assume constant shear stress acting on the fibre surface and neglect the effects of heat transfer [37] - [46] . The K-BKZ type of constitutive equation has been widely used in various studies on predicting the rheological behavior of viscoelastic materials. For example, Galante used the constitutive equation to describe viscoelastic effects in an integral equation of the K-BKZ type, suitable for polymer solutions and melts [40] . The problem with the constitutive equation of K-BKZ is that it is not fully applicable to predicting the nonlinear rheological behavior of viscoelastic materials [39] - [41] .

The behavior and properties of a non-Newtonian fluid within compressible flow are provided by the conservation of mass and momentum equations, respectively.

4. Governing Equations

The governing equations for the annulus flows are presented as follows.

Continuity equation for incompressible fluids:

where is the velocity vector.

Equation of momentum: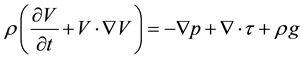

where is the density, is the pressure, and 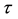is the stress tensor.

5. Constitutive Equations

There are many numerical representations for viscoelastic models. The most common models are Upper-con- vected Maxwell (UCM), Phan-Thien-Tanner (PTT), Oldroyd-B, Giesekus, K-BKZ and White-Metzner.

5.1. K-BKZ Model

The K-BKZ integral constitutive equation with multiple relaxation times describes and predicts the stresses within a fibrous suspension, solution, or molten polymer. Also, an extra term is added to the constitutive equation to account for the extra stresses due to the presence of fibres and to predict the orientation of a given fibre undergoing stresses within the suspension or molten [40] . The motivation for developing such a constitutive equation with these two considerations is to present an equation that can describe the rheological behavior of polymeric fibrous solutions and moltens while also to have a model, which can be used in numerical simulations.

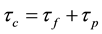
The fibre equation is:

where 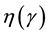is the viscosity of the polymer, is the shear rate, is the fibre volume fraction, 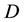and are the diameter and length of the fibre, 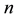is the number of the suspension, and is the average distance from a given fibre to its nearest neighbor [41] . Dinh and Armstrong proposed the following expression to calculate the distance between two fibres:

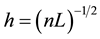for aligned systems

for random systems

Orientation tensor:

The polymer equation is:

where is the shear stress for the polymer, and are the relaxation times and relaxation moduli, is the number of relaxation modes, is the finger strain tensor, and is its first and second invariants. is the strain memory function, and the following formula is used, proposed by Papanastasiou et al.:

For simple shear flow, the strain-memory function is given as:

where and are nonlinear model constants to be determined from shear and elongation flow data, respectively. is the shear strain the Tstrain-memory function in simple shear flow is dependent on butnoton. This is expected since is viewed as a shear-thinning parameter, while is viewed as an elongational-thinning parameter [40] [41] .

5.2. Upper-Convected Maxwell Model (UCM)

UCM model is a differential generalization of the Maxwell model for the case of large deformations based on the upper-convected time derivative. The model can be written as:

is the tensor of the deformation rate

where is the relaxation time, is zero shear viscosity, and is tis he upper-convected time derivative of the stress tensor, which is expressed as:

The UCM constitutive model incorporates memory effects of materials, but its viscosity is constant at various shear rates [42] -[45] .

5.3. White-Metzner Model

The White-Metzner model is derived from the network theory of polymers (White and Metzner 1963). Modification of the viscosity and relaxation parameters as a function of the shear rate, leads to the White-Metzner model. This model exhibits shear thinning, not because of nonaffine motion, but because the relaxation is accelerated at high strain rates, where the relaxation is faster than any deformation [46] . The viscoelastic differential constitutive model takes the form:

where can be obtained from the experimental shear viscosity curve and the function can be obtained from the experimental first normal stress difference curve.

5.4. Phan-Thien-Tanner Model (PTT)

The PTT model refers to a quasi-linear viscoelastic constitutive equation, which is widely used in simulation of polymer solution flows. The original Phan-Thien Tanner equation was written using both of the following modifications simultaneously: the Gordon Schowalter derivative and the segment kinetics. It employs specific forms for the creation and destruction rates of the network junctions in the network theory of Lodge and Yamamoto [47] [48] . Although the Phan-Thien Tanner model over predicts both the shear viscosity at higher shear rates and the transient and extensional properties, it accurately predicts the zero shear viscosity and seems suitable for numerical simulations of polymer melts. It is worth noting that, compared to integral models such as the Bird- Carreau and Wagner models, differential models such as the PTT model provide robust numerical algorithms and exhibit good behavior in FEM simulations [47] . The interested reader is referred or more accurate comparison between the K-BKZ (as integral model) and the PTT model.

In the PTT model, the extra stress tensor is considered as the sum of the viscoelastic component, and the purely Newtonian component.

in which is given by:

where is the strain rate tensor.

The complete form of the PTT constitutive equation for the viscoelastic component is:

or

where the Oldroyd’s upper convective derivative isdefined by:

where represents the velocity matrix, is the transpose of the velocity matrix, and is the material derivative of the velocity matrix.

Analyzing the expression above, the first term represents the stress tensor transport and the transient part of the flow. In the second term, the slipping between the fluid polymeric chains is computed. The third term includes the elastic effects. Finally, the term on the right side of the equality represents the diffusive effects. is the stress tensor, the deformation-rate tensor, the fluid relaxation time, and the relaxation module. The parameter controls the amount of movement between the fluid polymeric chains [49] . For the model is named PTT Affine and the slipping between the polymeric chains is neglected. The function depends on the rate of creation and destruction of the links between the chains.Moreover, the PTT model incorporates the memory effect of materials and its viscosity can vary with the change of the shear rate. When is zero, PTT constitutive equation reduces to its simplified form (SPTT):

Phan-Thien and Tanner assumed specific forms for the creation and destruction rates of the network junctions and derived a constitutive equation containing two free parameters, and [48] . The exponential constitutive model takes the following form:

and are the adjustable parameters of the model.

The parameters and are the viscosity and relaxation time respectively, measured from the equilibrium relaxation spectrum of the fluid. They are not considered as adjustable parameters of the model. The PTT model can be solved using a single relaxation time or multiple relaxation times, similar to the Giesekus model. The linear form of the PTT model predicts shear thickening at high elongational rates, after which a plateau is reached [47] -[49] .

5.5. Giesekus-Leonov Model

Giesekus proposed a constitutive model based on a concept of configuration-dependent molecular mobility. In this model, the viscoelastic component of the extra stress tensor is represented with the following parameters, and. Owing to the highly nonlinear nature of the model equations, all of the properties need to be obtained numerically [50] -[55] .

The parameter is the dimensionless Giesekus-model mobility factor and controls the extensional viscosity and the ratio of second normal stress difference to the first one. The dimensionless The Giesekus-model mobility factor used to evaluate the anisotropic drag is represented by. For the model becomes the isotropic UCM model, while for the model is merely an anisotropic drag, and for the model re- presents shear-thinning behavior. The Giesekus model predicts the tension-thickening region for elongational flow, after which a plateau is reached; but it shows the existence of a tension-thinning region at high strain rates [56] -[59] .

5.6. Oldroyd-B Model

The Oldroyd-B model is a principal form of viscoelastic model:

where is the rate of deformation tensor, is the shear viscosity, is the relaxation time, and is the second relaxation parameter [60] -[62] . The Oldroyd-B model is mostly used to describe the rheological characteristics of polymer liquids composed at low concentration and moderate shear rates for high-viscosity Newtonian molecular weight polymer.

1) At the model simplifies to a second-order fluid with a vanishing second normal stress coefficient.

2) At the model reduces to the convected Maxwell model.

3) At the model reduces to a Newtonian fluid with viscosity.

6. Conclusions

Understanding the complex behaviour of polymer materials and interpreting it as one general equation requires a vast knowledge of the characteristics and formation of this complex type of material. Since rheometer does not provide the necessary information for all important rheological properties, constitutive equations are the best available tools for effective process control.

The development of valuable models for composite behavior and the exploration of appropriate constitutive equations to describe this complex behavior have been a high priority for many researchers. However, understanding the rheological behavior of viscoelastic composites is a redoubtable challenge.

The K-BKZ, PTT, Oldroyd-B, and Giesekus models will be widely studied and extended in future works. These models will be applied to the prediction and determination of the shear viscosity of viscoelastic composites as a function of shear stress and shear rate during extrusion and injection moulding processes.

Acknowledgements

This work was carried out with the support of Mitacs funding; the University of Toronto and the Ford Motor Company financially supported this study.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Anselm, O.O., Joseph, N.A. and Nduji, A.A. (2014) Characterization and Comparison of Rheological Properties of Agro Fiber Filled High-Density Polyethylene Bio-Composites. Open Journal of Polymer Chemistry, 4, 12-19. http://dx.doi.org/10.4236/ojpchem.2014.41002
[2]	Mohssine, M., Yves, F. and Mario, F. (2007) A Global Rheological Model of Wood Cantileveras Applied to Wood Drying. Wood Science and Technology, 41, 209-234.
[3]	Xie, F.W., Halley, P.J. and Avérous, L. (2012) Rheology to Understand and Optimize Processibility, Structures and Properties of Starch Polymeric Materials. Progress in Polymer Science, 37, 595-623.
[4]	Xiuying Q., Wei L., Hiroshi W., Kang S., Xiaodong, C. (2009) Rheological Behavior of Biocomposites of Silk Fibroin Fiber and Poly(ε-caprolactone): Effect of Fiber Network. Journal of Polymer Science Part B: Polymer Physics, 47, 1957-1970.
[5]	Zhang, Y., Lim, C.T., Ramakrishna, S. and Huang, Z.M. (2005) Recent Development of Polymer Nanofibers for Biomedical and Biotechnological Applications. Journal of Materials Science: Materials in Medicine, 16, 933-946.
[6]	http://pioneer.netserv.chula.ac.th/~sanongn1/course.html
[7]	Marynowski, K. (2006) Two-Dimensional Rheological Element in Modelling of Axially Moving Viscoelastic Web. European Journal of Mechanics—A/Solids, 25, 729-744.
[8]	Dealy, J.M. and Wissbrun, K.F. (1990) Melt Rheology and Its Role in Plastics Processing—Theory and Applications. Van Nostrand Reinhold, New York.
[9]	Ansari, M., Hatzikiriakos, S.G. and Mitsoulis, E. (2012) Slip effects in HDPE Flows. Journal of Non-Newtonian Fluid Mechanics, 167-168, 18-29.
[10]	Ansari, M., Alabbas, A., Hatzikiriakos, S.G. and Mitsoulis, E. (2010) Entry Flow of Polyethylene Melts in Tapered Dies. International Polymer Processing, 25, 287-296.
[11]	Owens, R.G. and Phillips, T.N. (2002) Computational Rheology. Imperial College Press, London.
[12]	Han, C. (2007) Rheology and Processing of Polymeric Materials, Vol. 2. Oxford University Press, Oxford.
[13]	Willett, J.L., Asberg, B.K. and Swanson, C.L. (1995) Rheology of Thermoplastic Starch: Effects of Temperature, Moisture Content, and Additives on Melt Viscosity. Polymer Engineering & Science, 35, 202-210. http://dx.doi.org/10.1002/pen.760350214
[14]	James, D.F. (2009) Boger Fluids. Annual Review of Fluid Mechanics, 41, 129-142. http://dx.doi.org/10.1146/annurev.fluid.010908.165125
[15]	Leszek, J. and Andrzej, Z. (2011) Mathematical Modelling of Pneumatic Melt Spinning of Isotactic Polypropylene. Part II. Dynamic Model of Melt Blowing. Fibres & Textiles in Eastern Europe, 16, 17-24.
[16]	Higashitani, K. and Pritchard, W.G. (1972) A Kinematic Calculation of Intrinsic Errors in Pressure Measurements Made with Holes. Transactions of the Society of Rheology, 16, 687. http://dx.doi.org/10.1122/1.549270
[17]	Tuna, N.Y. (1984) Finlayson. Journal of Rheology, 2879, 93.
[18]	Crochet, M.J. and Legat, V. (1992) The Consistent Streamline-Upwind/Petrov-Galerkin Method for Viscoelastic Flow Revisited. Journal of Non-Newtonian Fluid Mechanics, 42, 283-299. http://dx.doi.org/10.1016/0377-0257(92)87014-3
[19]	Dealy, J. and Wissbrun, K. (1999) Melt Rheology and Its Role in Plastics Processing: Theory and Applications. Kluwer Academic Publishers, Dordrecht.
[20]	Doraiswamy, D. (1988) The Origins of Rheology. DuPont iTechnologies, Wilmington.
[21]	Bird, R.B., Armstrong, R.C. and Hassager, O. (1987) Dynamics of Polymeric Liquids, Fluid Mechanics, Vol. 1. Wiley, New York.
[22]	Tucker III, C.L. and Advani, S.G. (1994) Processing of Short Fiber System. In: Flow and Rheology in Polymer Composites Manufacturing, Elsevier, Amsterdam, 147-202.
[23]	Grafe, T. and Graham, K. (2003) Polymeric Nanofibers and Nanofiber Webs: A New Class of Nonwovens. International Nonwovens Journal, 12, 51-55.
[24]	Zhou, C. and Kumar, S. (2010) Thermal Instabilities in Spinning of Viscoelastic Fibers. Journal of Non-Newtonian Fluid Mechanics, 165, 879-891. http://dx.doi.org/10.1016/j.jnnfm.2010.04.009
[25]	Jayaraman, K., Kotaki, M., Zhang, Y., Mo, X. and Ramakrishna, S. (2004) Recent Advances in Polymer Nanofibers. Journal of Nanoscience and Nanotechnology, 4, 52-65.
[26]	Letwimolnun, W., Vergnes, B., Ausias, G. and Carreau, P.J. (2007) Stress Overshoots of Organoclay Nanocomposites in Transient Shear Flow. Journal of Non-Newtonian Fluid Mechanics, 141, 167-179.
[27]	Collie, S.J., Gerritsen, M. and Jackson, P. (2001) A Review of Turbulence Modelling for Use in Sail Flow Analysis. School of Engineering Report No. 603, Auckland.
[28]	Denn, M.M. (2008) Continuous Drawing of Liquids to Form Fibers. Annual Review of Fluid Mechanics, 12, 365-387. http://dx.doi.org/10.1146/annurev.fl.12.010180.002053
[29]	Denn, M.M. (2008) Polymer Melt Processing: Foundations in Fluid Mechanics and Heat Transfer. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511813177
[30]	Krutka, H.M., Shambaugh, R.L. and Papavassiliou, D. (2008) Effects of the Polymer Fiber on the Flow Field from a Slot Melt Blowing Die. Industrial & Engineering Chemistry Research, 47, 935-945. http://dx.doi.org/10.1021/ie070871i
[31]	Tanner, R.I. (2000) Engineering Rheology. 2nd Edition, Oxford University Press, Oxford.
[32]	Denn, M.M., Petrie, C.J.S. and Avenas, P. (1975) Mechanics of Steady Spinning of a Viscoelastic Liquid. AIChE Journal, 21, 791-799. http://dx.doi.org/10.1002/aic.690210423
[33]	Nonaka, A., Trebotich, D., Miller, G.H., Graves, D.T. and Colella, P. (2009) A Higher-Order Upwind Method for Viscoelastic Fluids. Communications in Applied Mathematics and Computational Science, 4, 57-83. http://dx.doi.org/10.2140/camcos.2009.4.57
[34]	da Silva, L.J., Panzera, T.H., Velloso, V.R., Christoforo, A.L. and Scarpa, F. (2012) Hybrid Polymeric Composites Reinforced with Sisal Fibres and Silica Microparticles. Composites Part B, 43, 3436-3444. http://dx.doi.org/10.1016/j.compositesb.2012.01.026
[35]	Mitran, S.M. and Yao, L. (2007) A Double Projection Method for Incompressible Viscoelastic Flow. Technical Report, Department of Mathematics University of North Carolina, Chapel Hill.
[36]	Devereux, B.M. and Denn, M.M. (1994) Frequency Response Analysis of Polymer Melt Spinning. Industrial & Engineering Chemistry Research, 33, 2384-2390. http://dx.doi.org/10.1021/ie00034a020
[37]	Ellison, C.J., Phatak, A., Giles, D.W., Macosko, C.W. and Bates, F.S. (2007) Melt Blown Nanofibers: Fiber Diameter Distributions and Onset of Fiber Breakup. Polymer, 48, 3306-3316. http://dx.doi.org/10.1016/j.polymer.2007.04.005
[38]	Fisher, R.J. and Denn, M.M. (1977) Mechanics of Nonisothermal Polymer Melt Spinning. AIChE Journal, 23, 23-28. http://dx.doi.org/10.1002/aic.690230105
[39]	Ellyin, F., Vaziri, R. and Bigot, L. (2007) Predictions of Two Nonlinear Viscoelastic Constitutive Relations for Polymers under Multiaxial Loadings. Polymer Engineering & Science, 47, 593-607. http://dx.doi.org/10.1002/pen.20731
[40]	Galante, S.R. (1991) An Investigation of Planar Entry Flow Using a High Resolution Flow Birefringence Method. PhD Thesis, Garnegie Mellon University, Pennsylvania.
[41]	Burghardt, W.R. and Fuller, G.G. (1989) Note: End Effects in Flow Birefringence Measurements. Journal of Rheology, 33, 771-779. http://dx.doi.org/10.1122/1.550065
[42]	Kiriakidis, D.G., Park, H.J., Mitsoulis, E., Vergnes, B. and Agassant, J.F. (1989) A Study of Stress Distribution in Contraction Flows of an LLDPE Melt. Journal of Non-Newtonian Fluid Mechanics, 47, 339-356. http://dx.doi.org/10.1016/0377-0257(93)80057-I
[43]	Tan, D.H., Zhou, C., Ellison, C.J., Kumar, S., Macosko, C.W. and Bates F.S. (2010) Meltblown Fibers: Influence of Viscosity and Elasticity on the Diameter Distribution. Journal of Non-Newtonian Fluid Mechanics, 165, 892-900. http://dx.doi.org/10.1016/j.jnnfm.2010.04.012
[44]	Leszek, J. and Zbigniew, L. (2009) Mathematical Modelling of Pneumatic Melt Spinning of Isotactic Polypropylene. Part III. Computations of the Process Dynamics. Fibres & Textiles in Eastern Europe, 17, 75-80.
[45]	Altan, M.C., Advani, S.G., Guceri, S.I. and Pipes, R.B. (1989) On the Description of the Orientation State for Fiber Suspensions in Homogeneous Flows. Journal of Rheology, 33, 1129-1155. http://dx.doi.org/10.1122/1.550047
[46]	Marders, H., Vergnes, B., Demay, Y. and Agassant, J.F. (1992) Steady Flow of a White-Metzner Fluid in a 2-D Abrupt Contraction: Computation and Experiments. Journal of Non-Newtonian Fluid Mechanics, 45, 63-80. http://dx.doi.org/10.1016/0377-0257(92)80061-2
[47]	Phan-Thien, N. and Tanner, R.I. (1977) A New Constitutive Equation Derived from Network Theory. Journal of Non-Newtonian Fluid Mechanics, 2, 353-365. http://dx.doi.org/10.1016/0377-0257(77)80021-9
[48]	Phan-Thien, N. (1978) A Nonlinear Network Viscoelastic Model. Journal of Rheology, 22, 259-283. http://dx.doi.org/10.1122/1.549481
[49]	Wellington, M., Henrique, T., Admilson, T., Rigoberto, E.M. and André, L. (2007) Numerical Study of a PTT Viscoelastic Fluid Flow through Concentric Annular. 19th International Congress of Mechanical Engineering, Brasília, 5-9 November 2007.
[50]	Giesekus, H. (1982) A Simple Constitutive Equation for Polymer Fluids Based on the Concept of Deformation-Dependent Tensorial Mobility. Journal of Non-Newtonian Fluid Mechanics, 11, 69-109. http://dx.doi.org/10.1016/0377-0257(82)85016-7
[51]	Giesekus, H. (1985) Constitutive Equations for Polymer Fluids Based on the Concept of Configuration-Dependent Molecular Mobility: A Generalized Mean-Configuration Model. Journal of Non-Newtonian Fluid Mechanics, 17, 349- 372.
[52]	Mostafaiyan, M., Khodabandehlou, K. and Sharif, F. (2004) Analysis of a Viscoelastic Fluid in an Annulus Using Giesekus Model. Journal of Non-Newtonian Fluid Mechanics, 118, 49-55. http://dx.doi.org/10.1016/j.jnnfm.2004.01.007
[53]	Isaki, T., Takahashi, M., Takigawa, T. and Masuda, T. (1991) Comparison between Uniaxial and Biaxial Elongational Flow Behavior of Viscoelastic Fluids as Predicted by Differential Constitutive Equations. Rheologica Acta, 30, 530- 539. http://dx.doi.org/10.1007/BF00444371
[54]	Yarin, A.L., Sinha-Ray, S. and Pourdeyhimi, B. (2010) Meltblowing: II—Linear and Nonlinear Waves on Viscoelastic Polymer Jets. Journal of Applied Physics, 108, Article ID: 034913. http://dx.doi.org/10.1063/1.3457893
[55]	Müller, S., Kästner, M., Brummund, J. and Ulbricht, V. (2011) A Nonlinear Fractional Viscoelastic Material Model for Polymers. Computational Materials Science, 50, 2938-2949. http://dx.doi.org/10.1016/j.commatsci.2011.05.011
[56]	Luo, X.L. and Tanner, R.I. (1987) A Pseudo-Time Integral Method for Non-Isothermal Viscoelastic Flows and Its Application to Extrusion Simulation. Rheologica Acta, 26, 499-507. http://dx.doi.org/10.1007/BF01333733
[57]	Chauvière, C. and Owens, R.G. (2002) A Robust Spectral Element Method for Simulations of Time-Dependent Viscoelastic Flows, Derived from the Brownian Configuration Field Method. Journal of Scientific Computing, 17, 209-218. http://dx.doi.org/10.1023/A:1015152631360
[58]	Cirulis, J.T., Keeley, F.W. and James, D.F. (2010) Viscoelastic Properties and Gelation of an Elastin-Like Polypeptide. Journal of Rheology, 53, 1215-1228. http://dx.doi.org/10.1122/1.3177005
[59]	Oldroyd, J.G. (1950) On the Formulation of Rheological Equations of State. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 200, 523-541. http://dx.doi.org/10.1098/rspa.1950.0035
[60]	Oliveira, P.J. (2009) Alternative Derivation of Differential Constitutive Equations of the Oldroyd-B Type. Journal of Non-Newtonian Fluid Mechanics, 160, 40-46. http://dx.doi.org/10.1016/j.jnnfm.2008.11.013
[61]	Byron, R., Bird, R. and Robert, C. (1987) Armstrong, and Ole Hassager, Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics. 2nd Edition, John Wiley & Sons, New York.
[62]	Trebotich, D., Colella, P. and Miller, G.H. (2005) A Stable and Convergent Scheme for Viscoelastic Flow in Contraction Channels. Journal of Computational Physics, 205, 315-342. http://dx.doi.org/10.1016/j.jcp.2004.11.007