Some Methods to Maximize Extraction of Scientific Knowledge from Parallel Group Randomized Trials ()
1. Introduction
When the Consort Statement was published in 2001, it was emphasized that it was “… a continually evolving instrument” to improve the quality of reports of parallel group randomized trials” [1] [2] . The Consort Explanation and Elaboration item 20 stated that “...the difference between statistical and clinical importance should always be born in mind. Authors should particularly avoid the common error of interpreting a non-significant result as indicating equivalence of interventions” [1] [3] . Remember that “A difference is a difference, if it makes a difference”. This simple sentence contains and explains the important difference between a statistical and a clinical significance. The statistical significance is only related to a difference of at least the size of what an actual trial has found in outcome difference. It is not answering for all possible effect sizes and it does certainly not answer the question about the corresponding clinical significance or importance. The statistical and the clinical significance address two quite different questions the first being “is it a proven difference?” and the latter being “would it make a difference?” We lack a good way to measure the size of the clinical significance or importance, but in the following we suggest a simple, unbiased and reproducible way to procure information on the size of the clinical significance.
Next, null hypothesis significance testing and interpretation hold some surprises that were well summarized by Gliner, Leech and Morgan [4] : “the logic hypothesis testing is relatively difficult to understand… This is especially the case with regard to how to decide whether a …finding has practical importance”. Furthermore, “almost all of the textbooks fail to acknowledge that there are controversies surrounding null hypothesis testing” [4] . Usually, a study has shown some difference other than zero, and we ask: if the true difference were zero how often would this result happen (despite the fact that it has just happened). In case of a statistically non-sig- nificant result, the null hypothesis is not rejected which often leads to unfounded conclusions like: “the result did not reach statistical significance and it is therefore concluded, that there is no difference in outcome between the two treatments” [3] . The correct statement should be that it was not possible to reject the null hypothesis. It is worthy of a remark, that a statistically non-significant study has in fact missed detection of any possible real effect size! Obviously, very big outcome differences are hardly missed, but other alternative differences in effect sizes may be of clinical significance and thereby would be making a difference. In statistically, non-significant studies alternative questions may be relative differences of 10%, 20%, 30%, 40% or even 50%, and especially estimation of how often a study similar to the one in focus would have missed this (again: despite the fact that it has just happened). Therefore, the questions about clinical and statistical significances should be followed by questions of the credulity of statements on the risk of having missed different possible effect sizes. A relevant difference is a matter of opinion―and the power varies relative to this and cannot be described by only one measure. It may though easily be described in a generalized way by an operating characteristic curve showing the risk of not detecting a difference as being statistically significant (i.e. committing a type two error) as a function of any chosen minimally relevant difference. As this risk is declining with increasing sizes of minimal relevant difference the corresponding power and credulity is increasing. We therefore suggest depiction of the operating characteristic curve from which the credulity of statements on any possible effect size may be read.
Finally, it is important to recognize that rejection or acceptance of the null hypothesis may still be an error, but the risk of doing wrong with the null hypothesis may be assessed and may have grave consequences in form of cessation of use of harmful treatments. We therefore suggest inclusion of a figure depicting those risks.
2. Methods
The SORT OUT II is used as exemplification of our proposals and has previously been thoroughly described [5] [6] . In short, 2.098 patients with a total of 2.888 coronary lesions were randomized to receive one of the first two commercially available drug eluting stents―the sirolimus-eluting Cypher stent (Cordis/Johnson & Johnson, Miami Lake, Florida) (n = 1.065) or the paclitaxel-eluting Taxus stent (Boston Scientific Corp, Natick, Massachusetts) (n = 1.033). All subjects gave written informed consent and the study was approved by The National Committee on Health Research Ethics, 15 Finsensvej, DK-2000 Frederiksberg. The primary end point was the incidence of a major adverse cardiac event (MACE) consisting of the composite of cardiac death, myocardial infarction and target vessel revascularization.
The scientific knowledge may be maximized if the trial reporting system from CONSORT were expanded to encompass the following items:
First―the traditional quantification of the statistical significance with calculation of the hazard ratio (HR) and 95% confidence interval for HR, as already present in the CONSORT Guideline. In SORT OUT II the MACE occurred in 467 (22.3 %) of the patients, with 222 (20.8%) in the sirolimus-eluting stent group and 245 (23.7%) in the paclitaxel-eluting stent group. The vertical difference between the two curves of cumulated proportion of patients experiencing a MACE was statistically non-significant (log-rank test, Chi-square = 2.49, p = 0.11, HR 0.87, 95-% confidence interval 0.72 - 1.04) (Figure 1).
Second―and new―is quantification of the clinical significance/importance of an outcome difference or effect size: The area between the two curves of cumulated events will reflect an estimate of the net health gain with the superior treatment under the given and important presumption, that the present curves (Figure 1) should in fact be reflecting the genuine difference in outcome. The net health gain is shared among the patients in the best treatment group who experience a MACE but postpone its occurrence. The gain is dependent on the observation time (Figure 2). If the curves in Figure 1 were in fact a reflection of the real difference between the outcome of the two treatments and if all future patients were treated by the apparent superior treatment and were observed
![]()
Figure 1. The cumulated proportions of patients (%) with a major adverse cardiac event (MACE) for sirolimus- or paclitaxel-eluting stent groups by time (years, (6)).
![]()
Figure 2. The clinical significance quantifying the health gain with the superior device and depicted for major adverse cardiac events (MACE). Abscissa: observation time (days). Ordinate: the average days of postponement of a MACE if randomized to the sirolimus-eluting stent group as compared to the paclitaxel-eluting stent group (a negative value indicates that a MACE is reached sooner in the sirolimus-eluting stent group than in the paclitaxel-eluting stent group).
for X days then the patients experiencing an event would―at the average―postpone it by Y days as compared to the patients treated by the apparent worse treatment (Figure 2). Actually, this horizontal difference between the MACE curves showed that compared to patients in the paclitaxel-eluting stent group, the patients randomized to a sirolimus-eluting stent at the average would postpone the appearance of a MACE by 155 days with 5 years observation (Figure 2). The figure enables comparison to other studies with other observation lengths. It is left to the reader to decide whether a postponement of an event by a certain number of days would be perceived as being of clinical significance. Most important is that the magnitude of the clinical significance is now quantified!
Even if the vertical difference between two curves had been of statistical significance, the horizontal difference is still useful in order to determine if such proven difference also should have a magnitude of clinical significance that would be making a difference. The measure may be used in most trials. For instance, a randomized study on pancreatic cancer may statistically significantly reveal, that the number needed to treat to save one live would be 28. If the clinical significance was an average postponement of death by 21 days, then the statistically significant result might be perceived as a proven difference that is not making much of a difference. Therefore calculation of the postponement or the horizontal difference is a strong tool to measure the clinical relevance of a given “number needed to treat”.
[Computation of the horizontal difference: for each single day the area under each curve of cumulated proportion of patients experiencing an event is determined. The difference between these areas is calculated together with the cumulated area difference as a function of the observation time. The potential superiority is calculated as this cumulated area difference divided by the concomitant event rate from the event curve, which ends up in possessing the lowest cumulated event rate (in this case the sirolimus-eluting stent group).]
Third―is calculation of the type two error risks best depicted in an “operating characteristic curve” displaying the connection between increasing minimal relevant differences and the risk of not detecting such differences as being statistically significant [7] . This curve will enable the reader to select any personalized and individually chosen minimal relevant difference and concomitantly read what the corresponding risk of a non-signifi- cant result would be. By example, the risk that a repetition of a SORT OUT II like study should miss an absolute difference in MACE of at least 2.9% (i.e. the actual difference between the two curves) is at most 66% (Figure 3, top panel). This corresponds to a degree of credulity of 34% if we postulate from SORT OUT II, that “there is no difference between the two stents”. A study like SORT OUT II would in less than 7% of cases miss a relative difference of at least 25% as being statistically significant, and for such a size in relative difference our study has high credulity (93%) if it states that such a difference is seldom missed (Figure 3, bottom panel).
Fourth―is calculation of the risk of committing an error when either rejecting or accepting the null hypothesis (the delta error or the epsilon error respectively). These risks are dependent on the risk of committing a type one and a type two error but not the least on our trust in the correctness of the null hypothesis [8] . By inclusion of a figure depicting the risk of doing wrong with the null hypothesis as a function of our trust in the null hypothesis, it is possible to quantify the risk and leave it to the reader to select a personalized value of trust and read the corresponding risk.
If results from other trials make it possible that two treatments give different outcome then our belief in the null hypothesis is small. If for instance  then among 1000 trials the 100 would contain
then among 1000 trials the 100 would contain 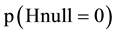 as “correct”. Of these 100 trials 5 will be false positive (when alfa = 0.05). Of the 900 other trials the 180 would be false negative (when beta = 0.20) and 720 be positive (Table 1). In total 5 out of 725 trials will be false positive (1%) which is the delta rate (Figure 4, the line denoted “delta (5.20)”) [8] . Likewise, the false negative rate will be
as “correct”. Of these 100 trials 5 will be false positive (when alfa = 0.05). Of the 900 other trials the 180 would be false negative (when beta = 0.20) and 720 be positive (Table 1). In total 5 out of 725 trials will be false positive (1%) which is the delta rate (Figure 4, the line denoted “delta (5.20)”) [8] . Likewise, the false negative rate will be 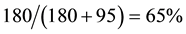 which is the epsilon rate (Figure 4, the line denoted “epsilon (5.20)” [8] . Consequently, the ones who strongly believe that there is a difference in outcome between two treatments and therefore only believes 10% in the correctness of the null hypothesis will only run a risk of 1% of committing a delta error if the trial is statistically significant and the null hypothesis consequently is rejected. If on the other hand the trial is statistically non-significant and the null hypothesis therefore accepted, then this would be an error in 65% of the cases (Figure 4, the line denoted “epsilon (5.20)”).
which is the epsilon rate (Figure 4, the line denoted “epsilon (5.20)” [8] . Consequently, the ones who strongly believe that there is a difference in outcome between two treatments and therefore only believes 10% in the correctness of the null hypothesis will only run a risk of 1% of committing a delta error if the trial is statistically significant and the null hypothesis consequently is rejected. If on the other hand the trial is statistically non-significant and the null hypothesis therefore accepted, then this would be an error in 65% of the cases (Figure 4, the line denoted “epsilon (5.20)”).
For the sake of illustration, we may fictitiously set the significance level to 0.11 which artificially would turn the SORT OUT II into a statistically significant study. A meta-analysis has shown that one stent is statistically significantly superior to the other which reduces our trust in the correctness of the null hypothesis to be for instance 10% [9] . If so be, a statistically significant result will only be a false positive result in 3% (delta error) and will merit rejection of the null hypothesis because we would be 97% sure that we are correct when we reject
![]()
![]()
Figure 3. Operating characteristic curves for major adverse cardiac events (MACE) for absolute (top panel) or relative difference (bottom panel). Abscissa: the absolute difference in MACE rate (%-points, top panel) or the relative difference in MACE rate (%, bottom panel). Ordinate: the risk of not detecting a difference of at least the size of x as being a statistical significant result given that a new study resembles the SORT OUT II with n1 = 1065, n2 = 1033, significance level 0.05 and a mutual event rate of MACE = 22.3%.
![]()
Table 1. Calculation of the a-posterior likelihood of having obtained either a false positive or a false negative result.
In brackets, the example contains 1000 virtual trials, alfa = 0.05 and beta = 0.20. TER = true effectiveness ratio by example a ratio of 0.1 is similar to a 10% trust in the correctness of the null hypothesis or . Delta =
. Delta =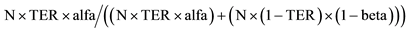 ; Reduced by
; Reduced by ; Likewise: Epsilon =
; Likewise: Epsilon =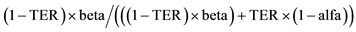 .
.
the null hypothesis (Figure 4, the line denoted “delta (11.66)”).
The SORT OUT II was a statistically non-significant study and estimation of the epsilon error is therefore the correct thing to do. Continuing with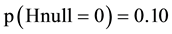 , there is 86% risk of committing an error if we accept the null hypothesis (Figure 4, the line denoted “epsilon (5.66)). If we only say, that SORT OUT II was ns
, there is 86% risk of committing an error if we accept the null hypothesis (Figure 4, the line denoted “epsilon (5.66)). If we only say, that SORT OUT II was ns
![]()
Figure 4. The risk of committing a delta or an epsilon error. Abcissa: the relative trust in the correctness of the null hypothesis of Hnull = 0. Ordinate: the risk of committing a delta error when rejection the null hypothesis is cases of statistically significant studies (the delta lines), or committing an epsilon error when accepting the null hypothesis in case of statistically non significant studies (the epsilon lines). In brackets (5.20) denotes alfa = 0.05 and beta = 0.20 and is an example with the values selected when SORT OUT II was planned. Delta (11.66) concerns alfa = 0.11 and beta = 0.66 which―if the significance level had been this chosen one―would have made the SORT OUT II a statistically significant study. Epsilon (5.20) was the values of alfa and beta in the planning phase and epsilon (5.66) denotes alfa = 0.05 and the beta value when SORT OUT II was terminated.
and as a consequence accept the null hypothesis and continue the clinical use of both stent types we would be translating the scientific evidence just like always!! But the ones who believe in a difference between the stent (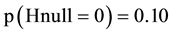 ) and use the epsilon curves―they would not be ready to accept the null hypothesis knowing this is 86 % likely to be wrong. Instead, they would immediately stop the usage of the paclitaxel-eluting stent until additional studies might emerge and clarify if it is safe to use that stent. In case the reader should be uncertain of which degree of trust to select there is another way to read the curves: From the epsilon (5.66) curve, it may be seen that if the trust is less than 41% then the risk of falsely accepting the null hypothesis would exceed 50%. Without estimation of the delta and epsilon error risk, it is almost impossible to stop the use of one treatment as a consequence of a statistically non-significant study. These considerations visualize how scientific knowledge may be maximized with quite immediate and unusual clinical consequences.
) and use the epsilon curves―they would not be ready to accept the null hypothesis knowing this is 86 % likely to be wrong. Instead, they would immediately stop the usage of the paclitaxel-eluting stent until additional studies might emerge and clarify if it is safe to use that stent. In case the reader should be uncertain of which degree of trust to select there is another way to read the curves: From the epsilon (5.66) curve, it may be seen that if the trust is less than 41% then the risk of falsely accepting the null hypothesis would exceed 50%. Without estimation of the delta and epsilon error risk, it is almost impossible to stop the use of one treatment as a consequence of a statistically non-significant study. These considerations visualize how scientific knowledge may be maximized with quite immediate and unusual clinical consequences.
3. Discussion
Explanatory remarks have been incorporated above and it suffices to say, that we have first of all created an unbiased and reproducible measure of clinical significance which has not previously been available. This measure is also useful to interpret the clinical importance of “the number needed to treat”. The estimation of the credulity of postulations on any effect size is especially useful when smaller trials have problems with the power and reach ns results because the operating characteristic curve enables extraction of the credulity on any effect size that should not be likely to be missed. Finally, the use of our a priory trust in the correctness of the null hypothesis has a strong impact on the risk of being in the wrong when rejecting or accepting the null hypothesis but these risks may be assessed and displayed in figures on delta and epsilon errors and used to make important clinical consequences more effective than what is generally happening now without estimation of these parameters.
All our suggestions cannot be extracted as single measures but it only takes three different depictions to enable the reader to choose any individually selected x-value and read the appropriate answers from the corresponding y-values. These depictions should therefore be part of reports on randomized trials and be itemized by the experts in their next revision of the CONSORT Guideline.
4. Conclusion
The reporting of the vertical difference between two cumulated event rates is used to estimate if there is a statistically significant difference. Expansion of the reporting with calculation of the horizontal differences may be utilized to estimate the magnitude of the clinical significance in an unbiased and reproducible way. The depiction of operating characteristic curves for both absolute and relative minimal relevant differences allows the reader to assess the credulity of not having missed any individually chosen minimal relevant difference. Finally, when other sources have brought knowledge of expected effect sizes, this may be used in the validation of the trial results by inclusion of a figure displaying the risks of delta and epsilon errors, which may induce quite other consequences to clinical practice than what simple null hypothesis testing would induce. These simple suggestions may be used to procure additional intelligence from each trial and may lead to improved quality of reports of parallel-group randomized trials and if the general reader of randomized trial is capable of understanding these few changes our suggestions may eventually lead to maximum scientific knowledge and better clinical practice―hopefully for the beneficial of the patients.
Acknowledgements
The Danish Heart Registry (DHR) has contributed with essential detection of invasive cardiac procedures.
Simon Day, the editor of Statistics in Medicine, has contributed importantly.
The SORT OUT II Investigators
Niels Bligaard, Leif Thuesen, Henning Kelbæk, Per Thayssen, Jens Aarøe, Peter R. Hansen, Jens F. Lassen, Kari Saunamäki, Anders Junker, Jan Ravkilde, Ulrik Abildgaard, Hans H. Tilsted, Thomas Engstrøm, Jan S. Jensen, Hans E. Bøtker, Søren Galatius, Carsten T. Larsen, Steen D. Kristensen, Lars R.Krusell, Steen Z. Abildstrøm, Evald H. Christiansen, Ghita Stephansen, R. N., Jørgen L. Jeppesen, John Godtfredsen, Søren Boesgaard, Jørgen L. Jeppesen, Anders M. Galløe.
NOTES
*Corresponding author.