Fibre-Reinforced Generalized Thermoelastic Medium under Hydrostatic Initial Stress ()
1. Introduction
The classical theories of thermo-elasticity involving infinite speed of propagation of thermal signals, contradict physical facts. During the last three decades, nonclassical theories involving finite speed of heat transportation in elastic solids have been developed to remove this paradox. In contrast to the conventional coupled thermo-elasticity theory which involves a parabolic-type heat transport equation, these generalized theories involving a hyperbolic-type heat transport equation are supported by experiments exhibiting the actual occurrence of wave-type heat transport in solids, called sound effect. The extended thermo-elasticity theory proposed by Lord and Shulman [2] incorporates a flux-rate term into Fourier’s law of heat conduction, and formulates a generalized form that involves a hyperbolic-type heat equation admitting finite speed of thermal signals. Muller [3] in a review of the thermodynamics of a thermoelastic solid, proposed an entropy production inequality, with the help of which he considered restrictions on a class of constitutive equations. A generalization of this inequality was proposed by Green and Laws [4]. Green and Lindsay [4] developed temperaturetype-dependent thermo-elasticity (TRDTE) theory by introducing relaxation time factors that does not violate the classical Fourier’s law of heat conduction and this theory also predicts a finite speed for heat propagation.
Barber [5] studied thermoelastic displacements and stresses due to a heat source moving over the surface of a half plane. Sherief [6] obtained components of stress and temperature distributions in a thermoelastic medium due to a continuous source. Dhaliwal et al. [7] investigated thermoelastic interactions caused by a continuous line heat source in a homogeneous isotropic unbounded solid. Chandrasekharaiah and Srinath [8] studied thermoelastic interactions due to a continous point heat source in a homogeneous and isotropic unbounded body. Sharma et al. [9] investigated the disturbance due to a time-harmonic normal point load in a homogeneous isotropic thermoelastic half-space. Sharma and Chauhan [10] discussed mechanical and thermal sources in a generalized thermoelastic half-space. Sharma et al. [11] investigated the steady-state response of an applied load moving with constant speed for infinite long time over the top surface of a homogeneous thermoelastic layer lying over an infinite half-space. Deswal and Choudhary [12] studied a two-dimensional problem due to moving load in generalized thermoelastic solid with diffusion.
Fibre-reinforced composites are used in a variety of structures due to their low weight and high strength. A continuum model is used to explain the mechanical properties of such materials. In the case of an elastic solid reinforced by a series of parallel fibres it is usual to assume transverse isotropy. In the linear case, the associated constitutive relations, relating infinitesimal stress and strain components, have five materials constants. The analysis of stress and deformation of fibrereinforced composite materials has been an important subject of solid mechanics for last three decades. Pipkin [13] and Rogers [14,15] did pioneer works on the subject. Craig and Hart [16] studied the stress boundary-value problem for finite plane deformation of a fibre-reinforced material. Sengupta and Nath [17] discussed the problem of surface waves in a fibre-reinforced anisotropic elastic media.. Singh and Singh [18] discussed the reflection of plane waves at the free surface of a fibre-reinforced elastic half-space. Singh [19] discussed the wave propagation in an incompressible transversely isotropic fibrereinforced elastic media. Singh [20] studied the effects of anisotropy on reflection coefficients of plane waves in fibre-reinforced thermoe-lastic solid. Kumar and Gupta [21] investigated a source problem in fibre-reinforced anisotropic generalized thermo-elastic solid under acoustic fluid layer.
The development of initial stresses in the medium is due to many reasons, for example, resulting from differences of temperature, process of quenching, shot pinning and cold working, slow process of creep, differential external forces, gravity variations, etc. The earth is assumed to be under high initial stresses. It is, therefore, of much interest to study the influence of these stresses on the propagation of stress waves. Biot [22] showed the acoustic propagation under initial stress, which is fundamentally different from that under a stress-free state. He has obtained the velocities of longitudinal and transverse waves along the co-ordinates axis only.
The wave propagation in solids under initial stresses has been studied by many authors for various models. The study of reflection and refraction phenomena of plane waves in an unbounded medium under initial stresses is due to Chattopadhyay et al. [23], Sidhu and Singh [24] and Dey et al. [25]. Montanaro [26] investigated the isotropic linear thermoelasticity with hydrostatic initial stress. Singh et al. [27], Singh [28] and Othman and Song [29] studied the reflection of thermoelastic waves from a free surface under a hydrostatic initial stress in the context of different theories of generalized thermoelasticity. Ailawalia et al. [30] investigated deformation in a generalized thermoelastic medium with hydrostatic initial stress. Ailawalia [31] obtained the components of displacement, stresses, temperature distribution of thermoelastic solid half-space under hydrostatic initial stress subjected to ramp-type heating and loading for G-N theory (type III).
The present paper is concerned with the investigations related to effect of hydrostatic initial stress in fibrereinforced generalized thermoelastic medium. Effects of hydrostatic initial stress and anisotropy are shown graphically on normal displacement, normal force stress and temperature distribution for Green-Lindsay [1] theory of thermoelasticity.
2. Basic Equations and Their Solutions
We consider a homogeneous thermally conducting transversely fibre-reinforced medium with hydros-tatic initial stress of infinite extent with cartesian coordinates system . To analyze the displacement components, stresses and temperature distribution at the interior of the medium, the continuum is divided into two half spaces defined by
. To analyze the displacement components, stresses and temperature distribution at the interior of the medium, the continuum is divided into two half spaces defined by
1) half space I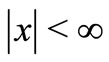 ,
,  ,
, 
2) half space II ,
,  ,
, 
if we restrict our analysis to the plane strain parallel to  -plane with displacement vector
-plane with displacement vector , then the field equations and constitutive relations for such a medium in the absence of body forces and heat sources are written as,
, then the field equations and constitutive relations for such a medium in the absence of body forces and heat sources are written as,
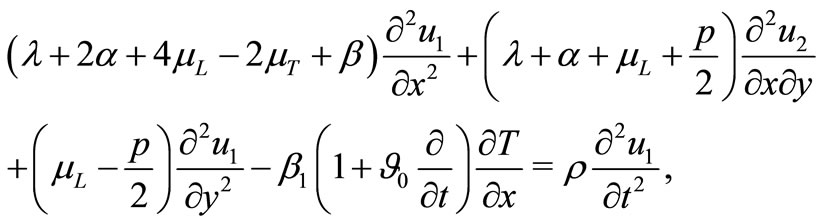 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
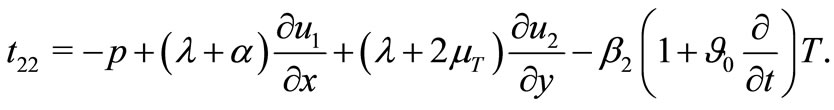 (7)
(7)
where

and 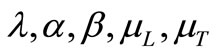 are material constants,
are material constants,  are coefficients of thermal conductivity,
are coefficients of thermal conductivity,  are coefficients of linear expansion,
are coefficients of linear expansion,  are thermal relaxation times,
are thermal relaxation times,  are the components of displacement vector,
are the components of displacement vector, 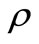 is the the mass density,
is the the mass density, 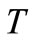 is the temperature change of a material particle,
is the temperature change of a material particle,  is the reference uniform temperature of the body and
is the reference uniform temperature of the body and  is the specific heat at constant strain.
is the specific heat at constant strain.
For simplification, we shall use the following nondimensional variables

 (8)
(8)
where

Substituting non-dimensional variables into Equations (1)-(3), we obtain (after dropping the primes)
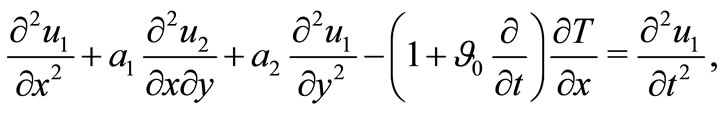 (9)
(9)
 (10)
(10)
 (11)
(11)
3. Normal Mode Analysis
The solution of the considered physical variable can be decomposed in terms of normal modes as the following form
 (12)
(12)
where  is the complex time constant and
is the complex time constant and 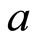 is the wave number in
is the wave number in  -direction.
-direction.
Using (12), Equations (9)-(11) take the form
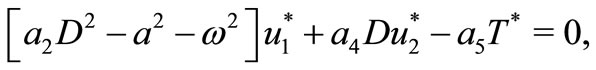 (13)
(13)
 (14)
(14)
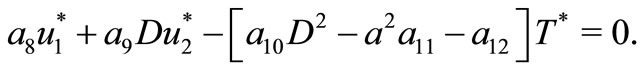 (15)
(15)
where

 (16)
(16)
Eliminating  and
and  from Equations (13)-(15), we obtain
from Equations (13)-(15), we obtain
 (17)
(17)
where
 (18)
(18)
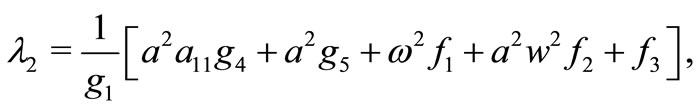 (19)
(19)
 (20)
(20)

 (21)
(21)
The solution of Equation (17) has the form
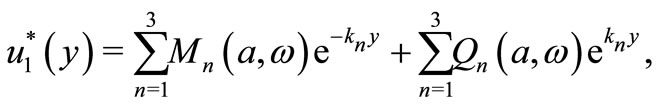 (22)
(22)
 (23)
(23)
 (24)
(24)
where ,
, 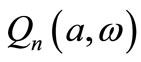 are some parameters depending on
are some parameters depending on 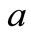 and
and .
.  are the roots of the characteristic equation (17).
are the roots of the characteristic equation (17).
Substituting from Equations (22)-(24) into (13)-(15), we obtain the following relations
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
where
 (29)
(29)
Thus the solution of Equations (1)-(3) are
 (30)
(30)
 (31)
(31)
 (32)
(32)
Normal mode analysis of the stress yields the following,
 (33)
(33)
 (34)
(34)
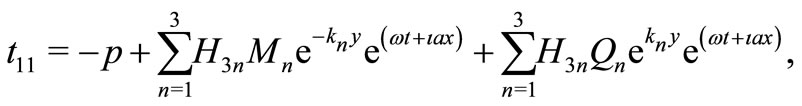 (35)
(35)
 (36)
(36)
4. Boundary Conditions
In order to determine the parameters  and
and , we consider the following boundary conditions at
, we consider the following boundary conditions at 
 (37)
(37)
where 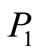 is the magnitude of mechanical force.
is the magnitude of mechanical force.
Using Equations (30)-(34) in boundary condition (37), we get six equations with six unknown parameters  and
and  as
as
 (38)
(38)
 (39)
(39)
 (40)
(40)
 (41)
(41)
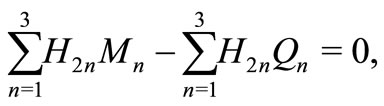 (42)
(42)
 (43)
(43)
Solving equations (38)-(43), the parameters 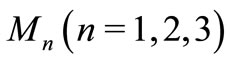 and
and  are derived as follows:
are derived as follows:

where  are defined in the appendix.
are defined in the appendix.
5. Particular Cases
5.1. Isotropic Generalized Thermoelastic Medium with Hydrostatic Initial Stress
Substituting ,
, 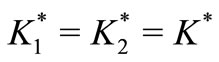 ,
,  and
and ,
, 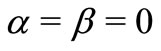 in Equations (30)-(36), we obtain the corresponding expressions of displacement, stress, and temperature distribution in isotropic generalized thermoelastic medium with hydrostatic initial stress.
in Equations (30)-(36), we obtain the corresponding expressions of displacement, stress, and temperature distribution in isotropic generalized thermoelastic medium with hydrostatic initial stress.
5.2. Fibre-Reinforced Generalized Thermoelastic Medium
Letting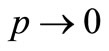 , the expressions (30)-(36) reduce to the case of fibre-reinforced generalized thermoelastic medium.
, the expressions (30)-(36) reduce to the case of fibre-reinforced generalized thermoelastic medium.
5.3. Isotropic Generalized Thermoelastic Medium
Substituting ,
,  ,
, 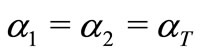 and
and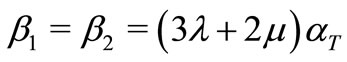 ,
, 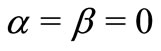 and letting
and letting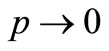 , the expressions (30)-(36) reduce to an isotropic generalized thermoelastic medium.
, the expressions (30)-(36) reduce to an isotropic generalized thermoelastic medium.
For all the cases discussed above the components of displacement, stresses and temperature distribution for the region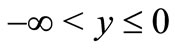 , are obtained by inserting
, are obtained by inserting  in Equations (30)-(36).
in Equations (30)-(36).
Similarly in the region , the components are obtained by inserting
, the components are obtained by inserting  in Equations (30)-(36).
in Equations (30)-(36).
6. Special Cases of Thermoelastic Theory
6.1. Equation of Coupled Thermoelasticity
The equations of the coupled thermoelasticity (C-T theory) are obtained when
 (44)
(44)
6.2. Lord-Shulman Theory
For the Lord-Shulman (L-S theory)
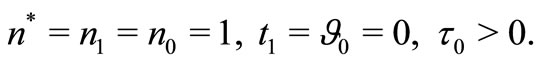 (45)
(45)
6.3. Green-Lindsay Theory
For Green-Lindsay(G-L theory),
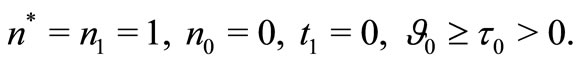 (46)
(46)
where  are the two relaxation times.
are the two relaxation times.
6.4. Equations of Generalized Thermoelasticity
The equations of the generalized thermoelasticity without energy dissipation (the linearized G-N theory of type II ) are obtained when
 (47)
(47)
Equations (1) and (2) are the same and equation (3) takes the form
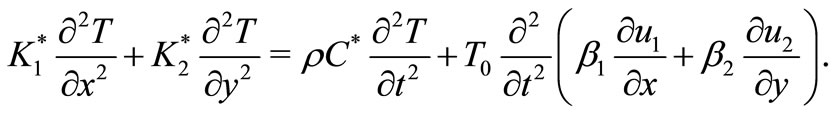 (48)
(48)
where 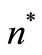 is constant with the dimension of
is constant with the dimension of  and
and  are characteristic constants of this theory.
are characteristic constants of this theory.
7. Numerical Results
With a view to illustrating the analytical procedure presented earlier, we now consider a numerical example for which computational results are given. The results depict the variations of normal displacement, normal force stress and temperature distribution in the context of G-L theory. For this purpose, we take the following values of physical constants as Singh [20]
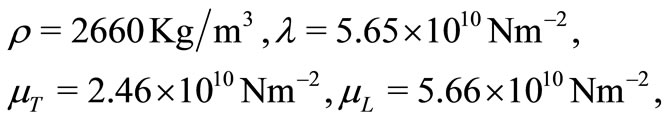



The computations are carried out on the surface  at
at . The graphical results for normal displacement
. The graphical results for normal displacement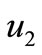 , normal force stress
, normal force stress  and temperature distribution
and temperature distribution  are shown in Figures 1-3 with
are shown in Figures 1-3 with ,
,  ,
, 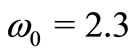 ,
,  ,
, 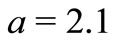 for a
for a
1) Fibre-reinforced generalized thermoelastic medium with hydrostatic initial stress (FRGTEHIS) by solid line.
2) Fibre-reinforced generalized thermoelastic medium without hydrostatic initial stress (FRGTEW-HIS) by solid line with centered symbol (*).
3) Isotropic generalized thermoelastic medium with hydrostatic initial stress (IGTEHIS) by dashed line.
4) Isotropic generalized thermoelastic medium without hydrostatic initial stress (IGTEWHIS) by dashed line with centered symbol (*).
These graphical results represent the solutions obtained by using the generalized theory with two relaxation times (G-L theory) by taking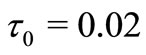 ,
, .
.
8. Discussions
The values of normal displacement for the case of FRGTEHIS increase sharply in the range and then

Figure 1. Variations of normal displacement u2 with horizontal distance x for mechanical force: (________) FRGTEHIS __ Fibre-reinforced generalized thermoelastic medium with hydrostatic initial stress, (---------) FRGTEWHISFibre-reinforced generalized thermoelastic medium without a hydrostatic initial stress, (*___*_____*) IGTEHIS __ isotropic generalized thermoelastic medium with a hydrostatic initial stress, (*----*----*) IGTEWHIS __ isotropic generalizedv thermoelastic medium without hydrostatic initial stress.

Figure 2. Variations of normal force stress t22 with horizontal distance x for mechanical force: (________)FRGTEHIS, (---------)FRGTEWHIS, (*___*_____*)IGTEHIS, (*----*------ *) IGTEWHIS. [see Figure 1 for explanation of symbols].
oscillate with distance. In case of IGTEHIS, the variations of normal displacement are very less in magnitude and for FRGTEWHIS, IGTEWHIS, these variations are quite uniform and at a particular point these variations are opposite in nature i.e. when one is on the zenith and the other one is on the lowest point. These variations are shown in Figure 1.
It is observed from Figure 2 that the variations of normal force stress for FRGTEHIS, FRGTEWHIS, IGTEHIS are similar in oscillating manner. The variation of normal force stress for IGTEWHIS is highly oscillating in nature in comparison to the variations obtained for FRGTEHIS, FRGTEWHIS, IGTEHIS.
The deformation of the body effects the change in temperature to a large extent as compared to normal displacement and normal force stress which is evident from Figure 3. Among all the mediums, the variation of temperature distribution is least oscillating for IGTEHIS.
9. Conclusions
1) The affects of anisotropy and hydrostatic initial stress are observed on all the quantities.
2) The variations of the temperature distribution are more oscillatory in nature than those of of normal force stress and normal displacement .
3) The variations for L-S and G-L theory of thermoelasticity are close, although the authors have de-

Figure 3. Variations of temperature distribution T with horizontal distance x for mechanical force: (________)FRGTEHIS, (---------)FRGTEWHIS, (*___*_____*) IGTEHIS, (*----*-----*)IGTEWHIS. [see Figure 1 for explanation of symbols].
picted the graphical results only for G-L theory.
Appendix



