Some Sequence of Wrapped Δ-Labellings for the Complete Bipartite Graph ()
1. Introduction
The desire to speed up secondary storage systems has lead to the development of disk arrays which achieve performance through disk parallelism. While performance improves with increasing numbers of disks, the chance of data loss coming from catastrophic failures, such as head crashes and failures of the disk controller electronics, also increases. To avoid high rates of data loss in large disk arrays, one includes redundant information stored on additional disks―also called check disks―which allows the reconstruction of the original data― stored on the so-called information disks―even in the presence of disk failures. These disk array architectures are known as redundant arrays of independent disks (RAID) (see [1] [2] ).
Optimal erasure-correcting codes using combinatorial framework in disk arrays are discussed in [1] [3] . For an optimal ordering, there are [4] [5] . Cohen et al. [6] gave a cyclic construction for a cluttered ordering of the complete graph. In the case of a complete graph, there are [7] [8] . Furthermore, in the case of a complete bipartite graph, Mueller et al. [9] gave a cyclic construction for a cluttered ordering of the complete bipartite graph by utilizing the notion of a wrapped Δ-labelling. In the case of a complete tripartite graph, we refer to [10] .
As Figure 1, we present the case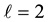 . For example, information disk 1 is associated to the check disks a and c. A 2-dimensional parity code can be modeled by the complete bipartite graph
. For example, information disk 1 is associated to the check disks a and c. A 2-dimensional parity code can be modeled by the complete bipartite graph 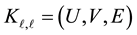 in the following way. The point set of
in the following way. The point set of 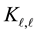 is partitioned into the two sets―U and V both having cardinality
is partitioned into the two sets―U and V both having cardinality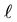 . Assign the points of U to the
. Assign the points of U to the 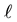 check bits corresponding to the rows and the points of V to the
check bits corresponding to the rows and the points of V to the 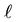 check bits corresponding to the columns. By definition, in
check bits corresponding to the columns. By definition, in 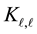 any point of U is connected with any point of V exactly on edge constituting the edge set E, i.e.,
any point of U is connected with any point of V exactly on edge constituting the edge set E, i.e.,  (see Figure 2).
(see Figure 2).
In this paper, we make label to the vertex of a bipartite graph. For example, we make label 1, 3, 0 and −1, respectively, to four vertices a, b, c and d of a bipartite graph in Figure 2. By such labelling, we get that the label of the edge 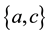 is
is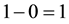 ; the label of the edge
; the label of the edge  is
is ; the label of the edge
; the label of the edge 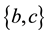 is
is 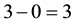 and the label of the edge
and the label of the edge 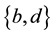 is
is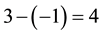 . The labellings
. The labellings ![]() of the upper vertices
of the upper vertices ![]() and the labellings
and the labellings ![]() of the lower vertices
of the lower vertices ![]() are sequences. The goal of this paper is to find new sequence in order to generate wrapped Δ-labellings as cluttered orderings for the complete bipartite graph. In Section 5, we give new sequence which we want. The new sequence we give is different from the sequences Mueller et al. [9] gave, though the same graphs in which these sequences are labeled.
are sequences. The goal of this paper is to find new sequence in order to generate wrapped Δ-labellings as cluttered orderings for the complete bipartite graph. In Section 5, we give new sequence which we want. The new sequence we give is different from the sequences Mueller et al. [9] gave, though the same graphs in which these sequences are labeled.
2. A Cluttered Ordering
In a RAID system disk writes are expensive operations and should therefore be minimized. In many applications there are writes on a small fraction of consecutive disks―say d disks―where d is small in comparison to k, the number of information disks. Therefore, to minimize the number of operations when writing to d consecutive information disks one has to minimize the number of check disks―say f―associated to the d information disks.
Let ![]() be a graph with
be a graph with ![]() vertices and edge set
vertices and edge set![]() . Let
. Let ![]() be a positive integer, called a window of G, and
be a positive integer, called a window of G, and ![]() a permutation on
a permutation on![]() , called an edge ordering of G. Then, given a graph G with edge ordering
, called an edge ordering of G. Then, given a graph G with edge ordering ![]() and window d, we define
and window d, we define ![]() to be the set of vertices which are connected by an edge of
to be the set of vertices which are connected by an edge of![]() ,
, ![]() , where indices are considered modulo m. The cost of accessing a subgraph of d consecutive edges is measured by the number of its vertices. An upper bound of this cost is given by the d-maximum access cost of G defined as
, where indices are considered modulo m. The cost of accessing a subgraph of d consecutive edges is measured by the number of its vertices. An upper bound of this cost is given by the d-maximum access cost of G defined as![]() . An ordering
. An ordering ![]() is a (d, f)-cluttered ordering, if it has d-maximum access cost equal to f. We are interested in minimizing the parameter f.
is a (d, f)-cluttered ordering, if it has d-maximum access cost equal to f. We are interested in minimizing the parameter f.
Let ![]() be a positive integer and let
be a positive integer and let ![]() denote the complete bipartite graph with
denote the complete bipartite graph with ![]() vertices and
vertices and ![]() edges. In the following, we identify the vertex set of
edges. In the following, we identify the vertex set of ![]() with
with![]() , where two vertices are connected by an edge iff they have different second components in
, where two vertices are connected by an edge iff they have different second components in![]() . The construction of (d, f)-cluttered orderings for
. The construction of (d, f)-cluttered orderings for ![]() with small positive integer f is based on two fundamental concepts. Firstly, we introduce the well-known concept of a Δ-labelling of a suitable bipartite subgraph from which one gets a decomposition of
with small positive integer f is based on two fundamental concepts. Firstly, we introduce the well-known concept of a Δ-labelling of a suitable bipartite subgraph from which one gets a decomposition of ![]() into isomorphic copies of this subgraph. Secondly, we define the concept of a (d, f)-movement which will lead to “locally” defined edge orderings of
into isomorphic copies of this subgraph. Secondly, we define the concept of a (d, f)-movement which will lead to “locally” defined edge orderings of![]() . This principle was implicitely used in [6] in case of the complete graph. In case of the complete bipartite graph, we refer to [9] .
. This principle was implicitely used in [6] in case of the complete graph. In case of the complete bipartite graph, we refer to [9] .
In the following, ![]() always denotes a bipartite graph with vertex set U which is partitioned into
always denotes a bipartite graph with vertex set U which is partitioned into
![]()
Figure 1. 2-dim. parity code and its parity check matrix.
two subsets denoted by V and W. Any edge of the edge set E contains exactly one point of V and W respectively. Let![]() , then a Δ-labelling of H with respect to V and W is defined to be a map
, then a Δ-labelling of H with respect to V and W is defined to be a map ![]() with
with ![]() and
and![]() , where each element of
, where each element of ![]() occurs exactly once in the difference list
occurs exactly once in the difference list
![]() (1)
(1)
Here, ![]() denotes the projection on the first component. In general, Δ-labellings are a well- known tool for the decomposition of graphs into subgraphs (see [11] ). In this context a decomposition is understood to be a partition of the edge set of the graph. In case of the complete bipartite graph, one has the following proposition.
denotes the projection on the first component. In general, Δ-labellings are a well- known tool for the decomposition of graphs into subgraphs (see [11] ). In this context a decomposition is understood to be a partition of the edge set of the graph. In case of the complete bipartite graph, one has the following proposition.
Proposition 1. ([9] ) Let ![]() be a bipartite graph,
be a bipartite graph, ![]() , and Δ be a Δ-labelling as defined above. Then there is a decomposition of the complete bipartite graph
, and Δ be a Δ-labelling as defined above. Then there is a decomposition of the complete bipartite graph ![]() into isomorphic copies of H.
into isomorphic copies of H.
For example, Figure 3 shows Δ-labellings of a graph ![]() with 3 edges leading to a decomposition of
with 3 edges leading to a decomposition of ![]() into isomorphic copies of
into isomorphic copies of ![]() such as Figure 4. Next, in order to move a graph H to an isomorphic copy such as Figure 5, we define the concept of a (d, f)-movement which can easily be generalized to arbitrary set system.
such as Figure 4. Next, in order to move a graph H to an isomorphic copy such as Figure 5, we define the concept of a (d, f)-movement which can easily be generalized to arbitrary set system.
Definition 1. Let G be a graph with edge set![]() , where n is positive integer, and let
, where n is positive integer, and let![]() ,
, ![]() with
with![]() . For a permutation
. For a permutation ![]() on
on ![]() define
define ![]() for
for![]() . Then, for some given a positive integer f, and a map
. Then, for some given a positive integer f, and a map ![]() is called a
is called a ![]() -movement from
-movement from ![]() to
to ![]() if
if![]() ,
, ![]() , and
, and![]() .
.
In order to assemble such (d, f)-movements of certain subgraphs to a (d, f)-cluttered ordering, we need some notion of consistency. Let ![]() be any bijection, then a (d, f)-movement
be any bijection, then a (d, f)-movement ![]() from
from ![]() to
to ![]() is called consistent with
is called consistent with ![]() if
if
![]() (2)
(2)
Now, for each ![]() one gets an automorphism
one gets an automorphism ![]() of the bipartite graph
of the bipartite graph ![]() defined by cyclic translation of the vertex set:
defined by cyclic translation of the vertex set:
![]()
Figure 3. A Δ-labelling of a graph ![]() with 3 edges.
with 3 edges.
![]() (3)
(3)
![]() . Obviously,
. Obviously, ![]() induces in a natural way an automorphism of the edge set of
induces in a natural way an automorphism of the edge set of ![]() which we
which we
also denote![]() . Then,
. Then, ![]() and
and![]() ,
,![]() . Next, we define a subgraph
. Next, we define a subgraph ![]()
by specifying its edge set![]() . Let
. Let![]() ,
, ![]() , where we fix some arbitrary edge ordering. We denote the restriction of the cyclic translation
, where we fix some arbitrary edge ordering. We denote the restriction of the cyclic translation ![]() to
to ![]() by
by ![]() which defines a bijection
which defines a bijection![]() .
.
Definition 2. With above notation, a (d, f)-movement of ![]() from
from ![]() to
to ![]() consistent with
consistent with ![]() will be denoted as
will be denoted as ![]() -movement from
-movement from ![]() consistent with the translation parameter
consistent with the translation parameter![]() .
.
According to Definition 1, such a (d, f)-movement is given by some permutation ![]() of the index set
of the index set![]() . By applying the cyclic translation
. By applying the cyclic translation ![]() one gets a graph
one gets a graph ![]() with edge set
with edge set
![]() ,
,![]() . We denote the restriction of
. We denote the restriction of ![]() to
to ![]() by
by ![]() which
which
defines a bijection
![]() (4)
(4)
Then ![]() also defines a
also defines a ![]() -movement of
-movement of ![]() from
from ![]() to
to ![]() consistent with
consistent with![]() . Using that
. Using that![]() ,
, ![]() , (see Defintion 1), we get, for
, (see Defintion 1), we get, for![]() ,
,
![]() (5)
(5)
Having such a consistent![]() , it is easy to construct a (d, f)-cluttered ordering of
, it is easy to construct a (d, f)-cluttered ordering of![]() . In short, one orders the edges of
. In short, one orders the edges of ![]() by first arranging the subgraphs of the decomposition along
by first arranging the subgraphs of the decomposition along ![]() and then ordering the edges within each subgraph according to
and then ordering the edges within each subgraph according to![]() .
.
Proposition 2. ([9] ) Let![]() ,
, ![]() , be a bipartite graph allowing some
, be a bipartite graph allowing some ![]() -labelling, and let
-labelling, and let ![]() be a translation parameter coprime to
be a translation parameter coprime to![]() . Furthermore, let
. Furthermore, let![]() ,
,![]() . If there is a (d, f)-movement from
. If there is a (d, f)-movement from ![]() consistent with
consistent with![]() , then there also is a (d, f)-cluttered ordering for the complete bipartite graph
, then there also is a (d, f)-cluttered ordering for the complete bipartite graph![]() .
.
3. Construction of Cluttered Orderings of ![]()
In this section, we define an infinite family of bipartite graphs which allow (d, f)-movements with small f. In order to ensure that these (d, f)-movements are consistent with some translation parameter![]() , we impose an additional condition on the Δ-labellings also referred to as wrapped-condition.
, we impose an additional condition on the Δ-labellings also referred to as wrapped-condition.
Let h and t be two positive integers. For each parameter f and t, we define a bipartite graph denoted by![]() . Its vertex set U is partitioned into
. Its vertex set U is partitioned into ![]() and consists of the following
and consists of the following ![]() vertices:
vertices:
![]()
The edge set E is partitioned into subsets![]() ,
, ![]() , defined by
, defined by
![]()
Figure 6 shows the edge partition of![]() . For the number of edges holds
. For the number of edges holds
![]() .
.
The t subgraphs defined by the edge sets Es, ![]() , and its respective underlying vertex sets are isomorphic to
, and its respective underlying vertex sets are isomorphic to![]() . Intuitively speaking, the bipartite graph
. Intuitively speaking, the bipartite graph ![]() consists of t “consecutive” copies of
consists of t “consecutive” copies of![]() , where the last h vertices of V and W respectively of one copy are identified with the first h vertices of V and W respectively of the next copy. Traversing these copies with increasing s will define a (d, f)-movement of
, where the last h vertices of V and W respectively of one copy are identified with the first h vertices of V and W respectively of the next copy. Traversing these copies with increasing s will define a (d, f)-movement of ![]() with small parameter f as is shown in the next proposition.
with small parameter f as is shown in the next proposition.
Proposition 3. ([9] ) Let h, t be pogitive integers. Let![]() ,
, ![]() , be the bipartite graph as de- fined above. Then, there is a (d, f)-movement of
, be the bipartite graph as de- fined above. Then, there is a (d, f)-movement of ![]() from
from ![]() to
to ![]() with
with ![]() and
and![]() .
.
By Proposition 1 a Δ-labelling of the graph ![]() will lead to a decomposition of the complete bipartite graph
will lead to a decomposition of the complete bipartite graph ![]() into
into ![]() isomorphic copies of
isomorphic copies of![]() , where
, where![]() . However, in general there is no
. However, in general there is no ![]() -movement consistent with some translation parameter
-movement consistent with some translation parameter![]() . To this means, we impose an additional condition on the Δ-labelling. The following definition generalizes and adapts the notion of a wrapped Δ-labelling to the bipartite case, which was introduced in [6] for certain subgraphs of the complete graph.
. To this means, we impose an additional condition on the Δ-labelling. The following definition generalizes and adapts the notion of a wrapped Δ-labelling to the bipartite case, which was introduced in [6] for certain subgraphs of the complete graph.
Definition 3. Let![]() ,
, ![]() , denote a bipartite graph and let
, denote a bipartite graph and let ![]() with
with![]() . A Δ- labelling Δ is called a wrapped Δ-labelling of H relative to X and Y if there exists a
. A Δ- labelling Δ is called a wrapped Δ-labelling of H relative to X and Y if there exists a ![]() coprime to
coprime to ![]() such that
such that
![]() (6)
(6)
as multisets in![]() . The parameter
. The parameter ![]() is also referred to as translation parameter of the wrapped Δ-labelling.
is also referred to as translation parameter of the wrapped Δ-labelling.
For the graphs![]() , we define
, we define ![]() and
and![]() . Furthermore, in the following we only consider wrapped Δ-labellings relative to X and Y for which the stronger condition
. Furthermore, in the following we only consider wrapped Δ-labellings relative to X and Y for which the stronger condition
![]() (7)
(7)
hold for![]() . Suppose we have such labelling Δ satisfying condition (7). Now,
. Suppose we have such labelling Δ satisfying condition (7). Now, ![]() ,
, ![]() , are isomorphic copies of
, are isomorphic copies of![]() . Furthermore,
. Furthermore, ![]() is isomorphic to
is isomorphic to ![]() consisting of the first d edges of
consisting of the first d edges of![]() . From condition (7) follows that the graph
. From condition (7) follows that the graph ![]() with edge set
with edge set ![]() can obviously identified with
can obviously identified with![]() . In addition, one easily checks that the (d, f)-movement of
. In addition, one easily checks that the (d, f)-movement of ![]() from Proposition 3 is consistent with the translation parameter
from Proposition 3 is consistent with the translation parameter![]() .
.
Proposition 4. ([9] ) Let ![]() be positive integers. From any wrapped Δ-labelling of
be positive integers. From any wrapped Δ-labelling of![]() , satisfying condition (7), one gets a (d, f)-cluttered ordering of the complete bipartite graph
, satisfying condition (7), one gets a (d, f)-cluttered ordering of the complete bipartite graph ![]() with
with![]() ,
, ![]() , and
, and![]() .
.
4. Sequences of Wrapped ![]() -Labellings for H(1; t), H(2; t) and H(h; 1)
-Labellings for H(1; t), H(2; t) and H(h; 1)
In this section, we construct some infinite families of such wrapped Δ-labellings. By applying Proposition 2 we get explicite (d, f)-cluttered orderings of the corresponding bipartite graphs. For these results in this section, we refer to [9] .
4.1. A Sequence for H(1; t)
We define a wrapped Δ-labelling of ![]() for any positive integer t.
for any positive integer t. ![]() has
has ![]() vertices
vertices
and 3t edges. For a fixed t, we define ![]() on the vertex set
on the vertex set ![]() as follows:
as follows:
![]()
where the integers in the first components are considered modulo 3t. We now compute the difference list ![]() of
of ![]() defined as in (1). Hence each element of
defined as in (1). Hence each element of ![]() appears in
appears in ![]() and the difference condition holds. Figure 3 illustrates the definition for the case t = 1.
and the difference condition holds. Figure 3 illustrates the definition for the case t = 1.
Obviously, the wrapped-condition (7) relative to ![]() and
and ![]() holds as well and the translation parameter
holds as well and the translation parameter ![]() is coprime to 3t for any t. Therefore, Δ defines the desired wrapped Δ-labelling of
is coprime to 3t for any t. Therefore, Δ defines the desired wrapped Δ-labelling of![]() .
.
Theorem 5. ([9] ) Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bi- partite graph ![]() with
with ![]() and
and![]() .
.
Theorem 6. ([9] ) Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bi- partite graph ![]() with
with ![]() and
and![]() ,
, ![]() ,
,![]() .
.
4.2. A Sequence for H(2; t)
We define a wrapped Δ-labelling of ![]() for any positive integer t.
for any positive integer t. ![]() has
has ![]() vertices and 10t edges. For a fixed t, a labelling Δ is a map
vertices and 10t edges. For a fixed t, a labelling Δ is a map ![]() on the vertex set
on the vertex set![]() . We specify the second component of Δ on the vertices
. We specify the second component of Δ on the vertices ![]() sequentially by the following list of 2t + 2 numbers:
sequentially by the following list of 2t + 2 numbers:
![]()
and, on the vertices ![]() by, similarly,
by, similarly,
![]()
where we set
![]()
All integers are considered modulo 10t. Note that ![]() and
and ![]() are coprime for all t and that the wrapped-condition (7) is obviously fulfilled. Thus, Δ defines a wrapped Δ-labelling.
are coprime for all t and that the wrapped-condition (7) is obviously fulfilled. Thus, Δ defines a wrapped Δ-labelling.
Theorem 7. ([9] ) Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bipar- tite graph ![]() with
with ![]() and
and![]() .
.
Theorem 8. ([9] ) Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bipar- tite graph ![]() with
with ![]() and
and![]() ,
, ![]() ,
,![]() .
.
4.3. A Sequence for H(h; 1)
We define in this section a wrapped Δ-labelling for ![]() for any positive integer h.
for any positive integer h. ![]() has
has
4h vertices and ![]() edges. We define the Δ-labelling
edges. We define the Δ-labelling ![]() on the vertex set
on the vertex set ![]()
by specifying the first component of Δ on the vertices ![]() sequentially by the following list of 2h numbers:
sequentially by the following list of 2h numbers:
![]()
and on the vertices ![]() by, similarly,
by, similarly,
![]()
where we set
![]()
All integers are considered modulo![]() . Obviously,
. Obviously, ![]() and
and ![]() are coprime for any positive integer h and the wrapped-condition (7) is fulfilled. Figure 7 illustrates the definition for the case
are coprime for any positive integer h and the wrapped-condition (7) is fulfilled. Figure 7 illustrates the definition for the case![]() . All numbers in
. All numbers in ![]() appear exactly once as difference of Δ which hence defines a wrapped Δ-labelling.
appear exactly once as difference of Δ which hence defines a wrapped Δ-labelling.
Theorem 9. ([9] ) Let ![]() be a positive integer. For all
be a positive integer. For all ![]() there is a (d, f)-cluttered ordering of the complete bipartite graph
there is a (d, f)-cluttered ordering of the complete bipartite graph ![]() with
with ![]() and
and![]() .
.
5. Our Result: A Sequence of a Wrapped ![]() -Labelling for
-Labelling for ![]()
In this section, we define a wrapped Δ-labelling of ![]() for any positive integer t.
for any positive integer t. ![]() has
has ![]() vertices and 21t edges. For a fixed t, a labelling Δ is a map
vertices and 21t edges. For a fixed t, a labelling Δ is a map ![]() on the vertex set
on the vertex set![]() . We specify the second component of Δ on the vertices
. We specify the second component of Δ on the vertices ![]() sequentially by the following list of
sequentially by the following list of ![]() numbers:
numbers:
![]()
and, on the vertices ![]() by, similarly,
by, similarly,
![]()
where we set
![]()
All integers are considered modulo 21t. Note that ![]() and
and ![]() are coprime for all positive integer t and that the wrapped-condition (7) is obviously fulfilled. Figure 8 illustrates the definition for the case t = 1.
are coprime for all positive integer t and that the wrapped-condition (7) is obviously fulfilled. Figure 8 illustrates the definition for the case t = 1.
We now compute the differences of Δ using the notation from (1):
![]()
![]()
![]()
![]()
![]()
![]()
We now compute the difference list![]() :
:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8-1)
(8-1)
![]() (8-2)
(8-2)
![]() (8-3)
(8-3)
![]() (9)
(9)
![]() (10)
(10)
![]() (11-1)
(11-1)
![]() (11-2)
(11-2)
![]() (11-3)
(11-3)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16-1)
(16-1)
![]() (16-2)
(16-2)
![]() (16-3)
(16-3)
![]() (17)
(17)
![]() (18)
(18)
![]() (19-1)
(19-1)
![]() (19-2)
(19-2)
![]() (19-3)
(19-3)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
From this one easily checks that the twenty-two lists cover all numbers in ![]() exactly once. Thus, Δ defines a wrapped Δ-labelling and by applying Proposition 4 we get the following result.
exactly once. Thus, Δ defines a wrapped Δ-labelling and by applying Proposition 4 we get the following result.
Theorem 10. Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bipartite graph ![]() with
with ![]() and
and![]() .
.
Using the same edge ordering of ![]() one gets the following theorem by enlarging the window d.
one gets the following theorem by enlarging the window d.
Theorem 11. Let t be a positive integer. For all t there is a (d, f)-cluttered ordering of the complete bipartite graph ![]() with
with ![]() and
and![]() ,
, ![]() ,
,![]() .
.
For example, we get a (21, 12)-cluttered ordering of![]() . For the graphs
. For the graphs![]() , this is a much better ordering than the (21, 16)-cluttered ordering from Theorem 6.
, this is a much better ordering than the (21, 16)-cluttered ordering from Theorem 6.
6. Conclusion
In conclusion, we give a new sequence for construction of wrapped Δ-labellings. Figure 7 and Figure 8 are the same as a graph, but they are different as a sequence. Cluttered orderings given by two sequences construct the different orderings for the complete bipartite graph![]() .
.
Acknowledgements
We thank the Editor and the referee for their comments.