Theories in Spin Dynamics of Solid-State Nuclear Magnetic Resonance Spectroscopy ()
1. Introduction
The Schrodinger equation is the fundamental equation of physics for describing quantum mechanical behavior. In classical physics, the Schrodinger equation predicts the future behavior of a dynamic system and plays an important role of Newton’s laws and conservation of energy [1] . In quantum mechanics, the Schrodinger equation is a partial differential time dependent equation that describes how the quantum state of a physical system changes. The acceptability of Schrodinger equation lies on its applicability in various fields of sciences such as physics, chemistry, and materials science [2] - [6] . For instance in field such as nuclear magnetic resonance (NMR), much effort still needs to be done to explore several problems using the time-dependent Schrodinger equation. These problems include but are not limited to medical imaging, crystallography, ultra short strong laser pulses, biological systems, chemical structures and composition, spin dynamics of superconductors and semiconductors [7] - [26] .
This short review presents some applications of major theories used in NMR spectroscopy such as the average Hamiltonian theory (AHT) and the Floquet theory (FLT), as well as the developing approaches including the Fer expansion (FE) and the Floquet-Magnus expansion (FME) [27] - [36] . We highlight potential future numerical and theoretical directions such as the time propagation operator calculated using Chebychev expansion and the transformation of Cayley [37] - [45] . The wealth of physical problems indicates the importance of having a general method for solving the time evolution of the density operator or the propagator operator in the case of NMR for instance. The density matrix 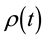 and its antecedent the propagator operator
and its antecedent the propagator operator 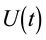 have been extensively used for many-body systems, such as atoms, molecules and nuclei; polarization of light and angular correlation experiments; the theory of masers and maser-like devices; the mean field techniques, such as Hartree-Fock and Thomas-Fermi approximations; the description of atoms and molecules in strong electromagnetic fields; resonance fluorescence and resonance Raman in the presence of intense field. Vast applications are present in electron and nuclear magnetic resonances [6] [46] - [48] . The physical insights provided by the theories presented in this review are illustrated by their applications. The following schematic diagram (Figure 1) shows the Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR [47] .
have been extensively used for many-body systems, such as atoms, molecules and nuclei; polarization of light and angular correlation experiments; the theory of masers and maser-like devices; the mean field techniques, such as Hartree-Fock and Thomas-Fermi approximations; the description of atoms and molecules in strong electromagnetic fields; resonance fluorescence and resonance Raman in the presence of intense field. Vast applications are present in electron and nuclear magnetic resonances [6] [46] - [48] . The physical insights provided by the theories presented in this review are illustrated by their applications. The following schematic diagram (Figure 1) shows the Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR [47] .
Solid-state NMR is a powerful method to elucidate molecular structure and dynamics in systems not amenable to characterization by other methodologies and its importance stands in its ability to accurately determine intermolecular distances and molecular torsion angles [34] [49] - [52] .
Methods developed over the past 3.5 years enabled us to obtain simplified calculations for the common form of Hamiltonian in solid-state NMR and multimode Hamiltonian in its generalized Fourier expansion Hamiltonian [34] . Based on these and other unpublished findings, we now believe that the FME provides a quick and efficient means to calculate higher order terms allowing the disentanglement of the stroboscopic observation and
![]()
Figure 1. Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR.
effective Hamiltonian that will be useful to describe spin dynamics processes in solid-state NMR and understand different synchronized or non-synchronized experiments [34] [52] - [55] . Furthermore, our first applications of FE approach to study interactions in solid-state NMR when irradiated with the magic-echo sequence support this goal [52] . The results of the first order 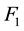 obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian,
obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian, 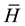 , in the sense of Magnus expansion under the circumstances:
, in the sense of Magnus expansion under the circumstances:
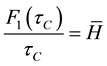 . A salient feature of the Fer and Magnus expansions stem from the fact that, when
. A salient feature of the Fer and Magnus expansions stem from the fact that, when 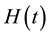 is an
is an
element in a given Lie algebra group, both approaches have the required structure and evolve in the desired group (Lie group). In addition, this is also true for their truncation to any order. We are thus poised to perform more work to ascertain the feasibility of Fer expansion in handling cases involving non-periodic and non-cyclic cases, and to use the expansion schemes of the Magnus (AHT) and the Fer expansions as numerical integrators for solving the time dependent Schrodinger equation which remains the central problem in quantum physics. Theoretical approaches in NMR are challenging, but the potential payoff is substantial, and could ultimately lead not only to a more accurate and efficient spin dynamics simulation, but also to the development of sophisticated RF pulse sequences, and understanding new experiments. Since the first demonstration of nuclear magnetic resonance in condensed matter in 1946 [56] [57] , the field of solid-state NMR has adopted only two milestones theoretical approaches in its history, theories which control the dynamics of spin systems: the average Hamiltonian theory (1968) [27] and the Floquet theory (1982) [30] [31] . However, compared to other spectroscopic techniques, the technique of NMR is well-established and will remain much a vibrant field of research due to its theoretical components driven by mathematicians, chemical and quantum physicists.
The overall goals of this review article is to support theories in NMR in order to continue to a) apply the average Hamiltonian theory to problems including (but not limited to): a class of symmetrical radio-frequency pulse sequences in the NMR of rotating solids, the symmetry principles in the design of NMR multiple-pulse sequences, the composite pulses, and the problems still unsolved such as the AHT for 3 spins [58] - [68] ; b) use the Floquet theory in the study of several magic-angle spinning (MAS) NMR experiments on spin systems with a periodically time-dependent Hamiltonian such as the multiple-multimode Floquet-theory in NMR [69] ; c) enhance the performance of the Floquet-Magnus expansion by considering fundamental questions that arise when dealing with this approach [34] . Using FME method, many interesting problems will be approached such as multi-mode Hamiltonian, rotational-resonance recoupling, continuous wave irradiation on a single species, DARR and MIRROR recoupling, C-type and R-type sequences, TPPM decoupling, etc. [54] [68] [69] ; d) use the Fer expansion to solve similar problems such as those solved using the AHT [32] ; e) explore potential future theoretical and numerical directions for the calculation of the time propagation and evolution operators using Chebychev expansion and Cayley transformation methods [37] [41] - [44] . It is noteworthy that unifying or combining two and more theories known in NMR will continue to provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a more efficient way that can be easily extended to all types of modulations.
2. Average Hamiltonian Theory
Since its first application in NMR in 1968 by Evans, Haeberlen and Waugh, the average Hamiltonian theory has evolved as a powerful technique of analysis in the development of high resolution NMR spectroscopy [27] [70] . The Magnus expansion forms the basis of AHT and has been systematically used in NMR, in particular in solid-state NMR where via AHT the ME has been instrumental in the development of improved techniques in NMR spectroscopy [35] [36] [70] . The approach of AHT is the main tool to control the dynamics of spin systems and to treat theoretical problems in solid-state NMR which have been used sometimes abusively [71] . The basic understanding of AHT involves a time dependent Hamiltonian 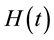 that governs the spin system evolution and describes the effective evolution by an average Hamiltonian
that governs the spin system evolution and describes the effective evolution by an average Hamiltonian 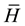 within a periodic time
within a periodic time . This is satisfied only if
. This is satisfied only if 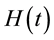 is periodic
is periodic  and the observation is stroboscopic and synchronized with period
and the observation is stroboscopic and synchronized with period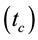 . This technique set the stage for stroboscopic manipulations of spins and spin interactions by radio-frequency pulses and also explains how periodic pulses can be used to transform the symmetry of selected interactions in coupled, many-spin systems considering the average or effective Hamiltonian of the RF pulse train [27] [34] [35] [72] - [75] . Wilhelm Magnus recognizes in his seminal paper of 1954 that his work was stimulated by results on the theory of linear operators in quantum mechanics. This shows that at its early stage, the Magnus expansion was strongly related to physics, and has been ever since then [72] . The central result of AHT is obtained by expressing the evolution propagator
. This technique set the stage for stroboscopic manipulations of spins and spin interactions by radio-frequency pulses and also explains how periodic pulses can be used to transform the symmetry of selected interactions in coupled, many-spin systems considering the average or effective Hamiltonian of the RF pulse train [27] [34] [35] [72] - [75] . Wilhelm Magnus recognizes in his seminal paper of 1954 that his work was stimulated by results on the theory of linear operators in quantum mechanics. This shows that at its early stage, the Magnus expansion was strongly related to physics, and has been ever since then [72] . The central result of AHT is obtained by expressing the evolution propagator 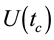 by an average Hamiltonian
by an average Hamiltonian  and using the Magnus expansion. The Magnus expansion provides a solution to the initial value problem
and using the Magnus expansion. The Magnus expansion provides a solution to the initial value problem
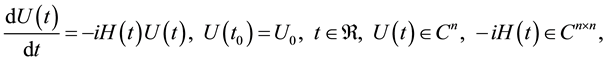 (1)
(1)
in terms of exponentials of combinations of the coefficient matrix![]() . The scalar case,
. The scalar case, ![]() (still valid
(still valid
for ![]() in some circumstances), has the general solution
in some circumstances), has the general solution![]() . If a term is added to the argument in the exponential such as
. If a term is added to the argument in the exponential such as![]() , then the Magnus expansion
, then the Magnus expansion
provides ![]() as an infinite series. A salient feature of the Magnus expansion is the fact that, when
as an infinite series. A salient feature of the Magnus expansion is the fact that, when ![]() belong to a given Lie algebra, if we express
belong to a given Lie algebra, if we express![]() , then
, then ![]() belong to the corresponding Lie group. By construction, the Magnus expansion lives in the Lie algebra. Furthermore, this is also true for their truncation to any order. In many applications this mathematical setting reflects important features of the problem. The method of AHT has been gradually applied to many theoretical problems in solid-state NMR such aspharmaceuticalproblemsolving and methodsdevelopment, symmetry in the design of NMR multiple- pulse sequences, composite pulses sequences, quantum computing, Magnus expansion as numericalintegrator, etc... [62] [65] [67] [72] [76] - [78] . Blanes and co-workersshownthatthe Magnus expansion can also be used as numerical method for solving Equation (1), with a good perspective of the overall performance of the numerical integrator provided by the efficiency diagram [35] . The efficiency plot is obtained by carrying out the numerical integrator with different time steps, corresponding to different numbers of evaluations of
belong to the corresponding Lie group. By construction, the Magnus expansion lives in the Lie algebra. Furthermore, this is also true for their truncation to any order. In many applications this mathematical setting reflects important features of the problem. The method of AHT has been gradually applied to many theoretical problems in solid-state NMR such aspharmaceuticalproblemsolving and methodsdevelopment, symmetry in the design of NMR multiple- pulse sequences, composite pulses sequences, quantum computing, Magnus expansion as numericalintegrator, etc... [62] [65] [67] [72] [76] - [78] . Blanes and co-workersshownthatthe Magnus expansion can also be used as numerical method for solving Equation (1), with a good perspective of the overall performance of the numerical integrator provided by the efficiency diagram [35] . The efficiency plot is obtained by carrying out the numerical integrator with different time steps, corresponding to different numbers of evaluations of![]() . However, AHT is not applicable to Hamiltonians with multiple basic frequencies: MAS and radiofrequency irradiation must be synchronized or time-scale separated, multiple irradiations must be synchronized or time-scale separated [79] [80] . Our recent validation of the AHT method probed with quadrupolar nuclei showed that the AHT method becomes less efficient to predict the dynamics of the spin system as the quadrupolar spin nuclei dimension increase [75] . This is attributed to the Hilbert space becoming very large and leading to the contribution of non-negligible higher order terms in the Magnus expansion being truncated.
. However, AHT is not applicable to Hamiltonians with multiple basic frequencies: MAS and radiofrequency irradiation must be synchronized or time-scale separated, multiple irradiations must be synchronized or time-scale separated [79] [80] . Our recent validation of the AHT method probed with quadrupolar nuclei showed that the AHT method becomes less efficient to predict the dynamics of the spin system as the quadrupolar spin nuclei dimension increase [75] . This is attributed to the Hilbert space becoming very large and leading to the contribution of non-negligible higher order terms in the Magnus expansion being truncated.
3. Floquet Theory
The FLT introduced to the NMR community in the early 1980’s simultaneously by Vegaand Maricqis another illuminating and powerful approach that offers a way to describe the time evolution of the spin system at all times and is able to handle multiple incommensurate frequencies [30] [31] [81] [82] . This theory provides a more general approach to AHT and has been applied satisfactorily to study important NMR phenomena [79] [80] [83] . The theory delineates the finite-dimensional time-dependent Liouville space onto an infinite-dimensional but time-independent Floquet space. The general description of the FLT is equally applicable to any nuclear spin systems. However, spin systems with large quadrupolar couplings may violate the convergence conditions for the expansions employed to evaluate the Floquet matrices. An important question to rise is the level of extension the FLT can be used in NMR without losing its conceptual framework. In other words, probing the validity of FLT for quadrupolar nuclei including those with spin I = 1, 3/2, 5/2, and 7/2 by analyzing for example a simple pulse sequence can be beneficial to the NMR community [75] . While the FLT scheme provides a more universal approach for the description of the full time dependence of the response of a periodically time-dependent system, it is most of the time impractical. Analytical calculations are limited to small spin systems and it is difficult to get physical insight from matrix representation. The full Floquet Hamiltonian has an infinite dimension and it is often not very intuitive to understand its implications on the time evolution of the spin system. Matrices for multi-mode Floquet calculations can become intractable. Massive reduction in dimensionality by truncation of the Fourier dimensions can introduce artifacts. In the literature, problems with up to three frequencies have been treated, but the demand of experiments that require four frequencies for a full description is increasing [69] [79] [80] . For instance, non-cyclic multiple-pulse sequences like two-pulse phase-modulated decoupling experiment acquire four frequencies under double rotation and there are some other obvious problems with four frequencies like triple-resonance CW radio frequency irradiation under MAS. Recent articles by Leskes et al., and Scholz et al. discussed extensively several MAS NMR experiments on spin systems with a periodically time-dependent Hamiltonian [69] [79] [80] . For many NMR experiments, understanding the spin dynamics requires a wise choice of the interaction frame in which the Hamiltonian is presented. Ramachandran and Griffin, and Schmidt and Vega introduced remarkable applications of Floquet theory in NMR [82] [83] . Indeed, bases employed in theoretical treatment of FLT and AHT do not extend to multiples spins or I > 1/2 systems, and fails to provide insights in to multiple-quantum NMR phenomena and polarization transfer experiments that involve relaxation. The multipole-multimode Floquet theory (MMFT) presented by Ramachandran and Griffin in its first application still remains a viable alternative for describing both coherent as well as incoherent effects observed in NMR experiments [83] . On one hand, Ramachandran and Griffin combined Shirley’s Floquet approach to the multipole theory proposed by Sanctuary in order toexpand any periodic time-dependent spin Hamiltonian, density operator, and Liouville superoperator in a Fourier series [83] - [85] . Substituting the Fourier expansions of the density operator and the Liouville super-operator in the Liouville equation, the following new set of coupled differential equations spanning an infinite dimensional vector space, with time-independent coefficients were obtained
![]() (2)
(2)
The notation ![]() includes the interaction coefficients as well as the spin and Fourier operators.
includes the interaction coefficients as well as the spin and Fourier operators.
Subsequently, the Floquet density operator and the Hamiltonian operator are represented by
![]() (3)
(3)
![]() (4)
(4)
The Floquet Hamiltonian ![]() is represented using an operator basis constructed by the direct product of
is represented using an operator basis constructed by the direct product of
operators defined both in the spin ![]() as well as the Fourier dimensions (
as well as the Fourier dimensions (![]() , corresponding to
, corresponding to ![]() time
time
modulation) with the off-diagonality represented by the indices ![]() and
and![]() , respectively. This approach provides analytical insights in spite of the infinite dimensionality of the problem which can be validated by describing an analytical solution in the form of effective Hamiltonians obtained via contact or van Vleck transformation procedure [83] . On the other hand, Schmidt and Vega defined a set of Floquet operators that simplify the use of the Floquet theory for single spin system under MAS condition by considering the single spin system that exhibit a chemical shift MAS Hamiltonian defined in the spin state manifold
, respectively. This approach provides analytical insights in spite of the infinite dimensionality of the problem which can be validated by describing an analytical solution in the form of effective Hamiltonians obtained via contact or van Vleck transformation procedure [83] . On the other hand, Schmidt and Vega defined a set of Floquet operators that simplify the use of the Floquet theory for single spin system under MAS condition by considering the single spin system that exhibit a chemical shift MAS Hamiltonian defined in the spin state manifold ![]() and the diagonalization of the Floquet Hamiltonian to the diagonalization of the sub-matrix diagonal matrices [82] . The signal and
and the diagonalization of the Floquet Hamiltonian to the diagonalization of the sub-matrix diagonal matrices [82] . The signal and
the Floquet transition amplitudes was evaluated to: ![]() with the
with the ![]() coefficients of
coefficients of
![]() expressed as
expressed as![]() . Furthermore, both authors extended their investigation to the dipolar
. Furthermore, both authors extended their investigation to the dipolar
coupled I = 1/2 spin pairs by evaluating two uncoupled homonuclear spins under magic angle sample spinning conditions ![]() with principal values of their chemical shift tensor
with principal values of their chemical shift tensor ![]() and Euler angles
and Euler angles ![]() [82] . In this case, the Hamiltonian evaluated is represented by means of the operators
[82] . In this case, the Hamiltonian evaluated is represented by means of the operators ![]() which connect different Floquet states, namely
which connect different Floquet states, namely![]() , with
, with ![]() differing in the Fourier index
differing in the Fourier index ![]() as well as the spin basis. Here, instead of calculating the correction terms, the method of contact transformation to calculate an effective Hamiltonian is used [86] . The contact transformation method is equivalent to the well-known Rayleigh-Schrodinger perturbation theory which provides corrections to zero order eigenvalues and eigenvectors. The unitary transformations are chosen in such a way that the off-diagonal operators due to interaction Hamiltonians are folded back to give diagonal contributions to the zero order Hamiltonian. As a result, a new Hamiltonian which is more effective, i.e., its eigenvalues are closer to the eigenvalues of the overall, untransformed Hamiltonian can be obtained. The transformation is done on the Hamiltonian so that by successive applications one obtains a Hamiltonian whose diagonal operators incorporate corrections from the interaction Hamiltonians [86] . The advantage of the method of contact transformation is that the correction is in the form of operators and therefore permits to define effective Hamiltonians which can be employed gainfully in pulse dynamics of rotating solids. An effective Hamiltonian is a simplified solution to the problem of finding the eigenvalues of the Floquet Hamiltonian. This method can also be useful when treating systems in which many spins are coupled. For instance, numerical diagonalization becomes quite difficult due to large dimensions of matrices when dealing with many spin coupled systems. Hence, the method of contact transformation gives the corrections in terms of operators and permits to restrict the spin basis, thereby reducing the size of matrices to be diagonalized in such systems.
as well as the spin basis. Here, instead of calculating the correction terms, the method of contact transformation to calculate an effective Hamiltonian is used [86] . The contact transformation method is equivalent to the well-known Rayleigh-Schrodinger perturbation theory which provides corrections to zero order eigenvalues and eigenvectors. The unitary transformations are chosen in such a way that the off-diagonal operators due to interaction Hamiltonians are folded back to give diagonal contributions to the zero order Hamiltonian. As a result, a new Hamiltonian which is more effective, i.e., its eigenvalues are closer to the eigenvalues of the overall, untransformed Hamiltonian can be obtained. The transformation is done on the Hamiltonian so that by successive applications one obtains a Hamiltonian whose diagonal operators incorporate corrections from the interaction Hamiltonians [86] . The advantage of the method of contact transformation is that the correction is in the form of operators and therefore permits to define effective Hamiltonians which can be employed gainfully in pulse dynamics of rotating solids. An effective Hamiltonian is a simplified solution to the problem of finding the eigenvalues of the Floquet Hamiltonian. This method can also be useful when treating systems in which many spins are coupled. For instance, numerical diagonalization becomes quite difficult due to large dimensions of matrices when dealing with many spin coupled systems. Hence, the method of contact transformation gives the corrections in terms of operators and permits to restrict the spin basis, thereby reducing the size of matrices to be diagonalized in such systems.
4. Fer Expansion
Analysis and numerical implementation of Magnus expansions is not a trivial task. Therefore, an alternative to the Magnus expansion which is called the Fer expansion can be useful for solving the time-dependent Schrodinger differential equation. This approach was formulated more than half a century ago by Fer and wasrecently introduced to the NMR community by Madhu and Kurur [32] [33] . This expansion is still in its infancy in NMR and can be considered to be complimentary to the Magnus expansion (AHT). Indeed, from the point of view of physical applications, the Magnus expansion has been extensively used in a variety of issues, while the Fer expansion has been either ignored or misquoted until recently [87] . While the efficiency of Fer expansion seems obvious, more effort is still required to allow the approach to overcome difficulties such as cases involving non- periodic and non-cyclic cases. More quantitative work need to be performed in order to bring out the salient features of the Fer expansion and explore its use in solid-state NMR and in many other theoretical areas. The Fer expansion approximates the solution to the initial value problem (Equation (1)) by a product of matrix exponent
tials. The expansion is generated by the recursive scheme, ![]() , and the iterative formula are
, and the iterative formula are ![]() and
and![]() , where
, where![]() .
.
The Fer expansion involves a series of nested commutators resulting in![]() . The Fer expansion differs to the Magnus approach in the form of the correction terms. The iteration process can continue easily when the initial values of
. The Fer expansion differs to the Magnus approach in the form of the correction terms. The iteration process can continue easily when the initial values of ![]() and
and ![]() are found. One major advantage of the Fer expansion over the AHT is that only an evaluation of nested commutators is required in the calculation of
are found. One major advantage of the Fer expansion over the AHT is that only an evaluation of nested commutators is required in the calculation of![]() . The Magnus expansion requires the calculation of nested commutators and their integrals to obtain the correction terms of a Hamiltonian. Blanes et al. had proved the convergence of the Fer expansion and showed that the convergence of Fer expansion is much faster than that of Magnus expansion [35] [36] [87] . Madhu and Kurar also highlighted the observations such that the calculation of a term like
. The Magnus expansion requires the calculation of nested commutators and their integrals to obtain the correction terms of a Hamiltonian. Blanes et al. had proved the convergence of the Fer expansion and showed that the convergence of Fer expansion is much faster than that of Magnus expansion [35] [36] [87] . Madhu and Kurar also highlighted the observations such that the calculation of a term like ![]() will contain several of the important signatures of the various higher- order terms in Magnus expansion, where all terms need to be calculated independently [32] . In addition, they mentioned that, the calculation of the infinite number of commutators, although looking imposing, may turn out to be simpler to handle in most experimentally interesting cases due to the fast convergence and the negligible value of many of the commutators. Both approaches (Fer and AHT) may be complimentary and the aspects of the problem at hand might eventually dictate the approach to be chosen [32] . The Fer expansion has been recently applied to the calculations of Block-Siegert shift in NMR, the analysis of heteronuclear decoupling in solid-state NMR, and the study of various interactions in solid-state NMR when irradiated with magic echo pulse sequence [32] [52] . Blanes and co-workers used Fer expansion as numerical method for solving time dependent Schrodinger equation. A good perspective of the overall performance of their given numerical integrator is provided by the efficiency diagram with the results better illustrated in a double logarithmic scale [35] . The Fer expansion has also been used to solve many physical situations such as classical time-dependent Hamiltonian systems [88] [89] . Furthermore, subtle aspects of FE including, the convergence issue, the degree of computational involvement, and the application to coupled networks of spins, with regard to NMR still need to be tackle [32] [88] .
will contain several of the important signatures of the various higher- order terms in Magnus expansion, where all terms need to be calculated independently [32] . In addition, they mentioned that, the calculation of the infinite number of commutators, although looking imposing, may turn out to be simpler to handle in most experimentally interesting cases due to the fast convergence and the negligible value of many of the commutators. Both approaches (Fer and AHT) may be complimentary and the aspects of the problem at hand might eventually dictate the approach to be chosen [32] . The Fer expansion has been recently applied to the calculations of Block-Siegert shift in NMR, the analysis of heteronuclear decoupling in solid-state NMR, and the study of various interactions in solid-state NMR when irradiated with magic echo pulse sequence [32] [52] . Blanes and co-workers used Fer expansion as numerical method for solving time dependent Schrodinger equation. A good perspective of the overall performance of their given numerical integrator is provided by the efficiency diagram with the results better illustrated in a double logarithmic scale [35] . The Fer expansion has also been used to solve many physical situations such as classical time-dependent Hamiltonian systems [88] [89] . Furthermore, subtle aspects of FE including, the convergence issue, the degree of computational involvement, and the application to coupled networks of spins, with regard to NMR still need to be tackle [32] [88] .
5. Floquet-Magnus Expansion
The Floquet Magnus expansion is a new theoretical tool for describing spin dynamics recently introduced in solid-state NMR and spin physics [34] - [36] . This unique approach (FME) is an extension of the popular Magnus expansion and average Hamiltonian theory and is useful to shed new lights on AHT and FLT [27] [28] . The aims of the FME is to bridge the AHT to the Floquet Theorem but in a more concise and efficient formalism [34] . Calculations can then be performed in a finite-dimensional Hilbert space instead of an infinite dimensional space within the Floquet theory. We expected that the FME will provide means to more accurately and efficiently perform spin dynamics simulation and for devising new RF pulse sequence. We also expect the FME to explore physical implementations of quantum information processing (QIP) and introduce the basic background for understanding applications of NMR in QIP and explain their successes, limitations and potential. The FME provides a quick means to calculate higher order term allowing the disentanglement of the stroboscopic observation ![]() and effective Hamiltonian
and effective Hamiltonian ![]() that will be useful to describe spin dynamics at all times in solid- state NMR and understand different synchronized or non-synchronized experiments. The FME offers a simple way to handle multiple incommensurate frequencies and thus open perspectives to deal with multi-mode Hamiltonian in the Hilbert space. This approach can provide new aspects not present in AHT and FT such as recursive expansion scheme in Hilbert space that can facilitate the development of new or improvement of existing pulse sequence. This scheme controls the spin dynamic systems in solid state NMR and makes use of its unique solution that has the required structure and evolves in the desired Lie group. In the first order, all three theoretical approaches (AHT, FLT, and FME) are equivalent, which corresponds to the popular average Hamiltonian,
that will be useful to describe spin dynamics at all times in solid- state NMR and understand different synchronized or non-synchronized experiments. The FME offers a simple way to handle multiple incommensurate frequencies and thus open perspectives to deal with multi-mode Hamiltonian in the Hilbert space. This approach can provide new aspects not present in AHT and FT such as recursive expansion scheme in Hilbert space that can facilitate the development of new or improvement of existing pulse sequence. This scheme controls the spin dynamic systems in solid state NMR and makes use of its unique solution that has the required structure and evolves in the desired Lie group. In the first order, all three theoretical approaches (AHT, FLT, and FME) are equivalent, which corresponds to the popular average Hamiltonian,
![]() . The FME approach can be considered as an improved AHT or a new version of
. The FME approach can be considered as an improved AHT or a new version of
FLT that could be very useful in simplifying calculations and providing a more intuitive understanding of spin dynamics processes. The approach of FME is essentially distinguished from other theories with its famous function ![]()
![]() which provides an easy and alternative way for evaluating the spin behavior in between the stroboscopic observation points. The function
which provides an easy and alternative way for evaluating the spin behavior in between the stroboscopic observation points. The function ![]() available only in the FME scheme will be useful to describe the spin dynamics in solid-state NMR and understanding different synchronized or non-syn- chronized experiments. The relationship with the regular Magnus expansion can be obtained from,
available only in the FME scheme will be useful to describe the spin dynamics in solid-state NMR and understanding different synchronized or non-syn- chronized experiments. The relationship with the regular Magnus expansion can be obtained from, ![]() [34] - [36] . This points out that it is only in the case
[34] - [36] . This points out that it is only in the case![]() , that the FME gives the AHT as provided by the Magnus expansion,
, that the FME gives the AHT as provided by the Magnus expansion,![]() . Therefore, the general approach of the AHT gives also
. Therefore, the general approach of the AHT gives also
the option of a more general representation of the FME with![]() . Furthermore, the function
. Furthermore, the function ![]() is connected to the appearance of features like spinning sidebands in MAS. The general formulas for the contribution of the FME are given by:
is connected to the appearance of features like spinning sidebands in MAS. The general formulas for the contribution of the FME are given by:
![]() , with
, with ![]() [34] . Symbolic calculation software can enable
[34] . Symbolic calculation software can enable
formal derivation of higher order terms. In the above equations, the ![]() functions with
functions with![]() , re- presents the nth order term of the argument of the operator that introduces the frame such that the spin system operator is varying under the time independent Hamiltonian
, re- presents the nth order term of the argument of the operator that introduces the frame such that the spin system operator is varying under the time independent Hamiltonian![]() . The evaluation of the function
. The evaluation of the function ![]() is useful in many different ways, for instance, in rotating experiment of NMR, this function can be useful to quantify the level of productivity of double quantum terms [54] [55] . The FME propagator is given by:
is useful in many different ways, for instance, in rotating experiment of NMR, this function can be useful to quantify the level of productivity of double quantum terms [54] [55] . The FME propagator is given by:![]() . Here the constraint of stroboscopic observation is removed.
. Here the constraint of stroboscopic observation is removed. ![]() is the operator that introduces the frame that varies under the time independent Hamiltonian
is the operator that introduces the frame that varies under the time independent Hamiltonian![]() . The function
. The function ![]() given explicitly above is the argument of the operator
given explicitly above is the argument of the operator ![]() such that:
such that:![]() . Like the FLT, the FME describes the time evolution of the spin system at all times. Forvarious interactions in NMR, we recently calculated the first order function
. Like the FLT, the FME describes the time evolution of the spin system at all times. Forvarious interactions in NMR, we recently calculated the first order function ![]() that provide an easy way for evaluating the spin system evolution [52] . The evaluation of
that provide an easy way for evaluating the spin system evolution [52] . The evaluation of ![]() is useful especially for the analysis of the non-stroboscopic evolution. We also found that the second order
is useful especially for the analysis of the non-stroboscopic evolution. We also found that the second order ![]() is small in comparison to the first order
is small in comparison to the first order![]() , and will be less useful in many cases [54] [55] .
, and will be less useful in many cases [54] [55] .
5.1. Common Form of Hamiltonian in Solid-State NMR
For the sake of simplicity, we considered the Hamiltonian: ![]() which is a com
which is a com
mon form of Hamiltonian in solid-state NMR. ![]() is the Zeeman interaction,
is the Zeeman interaction, ![]() are the lattice parts of the internal interaction which encode its orientational dependence with respect to the magnetic field,
are the lattice parts of the internal interaction which encode its orientational dependence with respect to the magnetic field, ![]() are
are
second rank m-order spherical tensor describing the spin system as defined by ![]() . The static
. The static
perturbation theory (SPT) in terms of the irreducible tensor operators gives the diagonal Hamiltonian,
![]() [71] . Discrepancies between AHT and FT appear in the
[71] . Discrepancies between AHT and FT appear in the
interaction frame where the Hamiltonian becomes time-dependent
![]() . The FME provides an expansion in the rotating frame which
. The FME provides an expansion in the rotating frame which
is in agreement with the static perturbation theory and Van Vleck transformations. This is not the case of the Magnus expansion. This agreement can be easily explained by the connection that exists between the SPT and
FME propagators written as![]() ,
, ![]() , respectively. This means that under the criterion
, respectively. This means that under the criterion ![]() both propagators describe the same evolution at any time [34] .
both propagators describe the same evolution at any time [34] .
5.2. Extension to Multimode Hamiltonian
Considering the generalized Fourier expansion of the Hamiltonian ( ![]() represented by the frequency indices)
represented by the frequency indices)![]() , we obtain
, we obtain ![]() and
and![]() . Simi-
. Simi-
larly, calculation of second order terms is straightforward [34] .These expressions highlight the fact that the multimode Hamiltonian case can be easily treated in Hilbert space with the FME.
5.3. BABA and C7
For example, applying the first contribution terms of FME to the dipolar Hamiltonian when irradiated with the BABA (Figure 2 and Figure 3) and sevenfold symmetric radiofrequency pulse sequences shown in Figure 3 of
reference [54] , we generated the plots (![]() and
and ![]() versus the dimensionless numbers
versus the dimensionless numbers![]() ) of
) of
the degree of recoupling magnetic dipolar between nuclear spins which is useful for preparing and detecting double quantum coherence [54] [55] [90] . Therefore, the study of the amplitude of DQ terms can be considered as a viable approach for controlling the complex spin dynamics of a spin system evolving under the dipolar in-
teraction of BABA and C7 pulse sequences. The size of ![]() determine the amplitude of the DQ coherence,
determine the amplitude of the DQ coherence,
which indicates the degree of efficiency of the scheme. In reference [54] , a closer look at Figure 4(c) and Figure 5(c) shows that the magnitude of ![]() is small comparatively to the magnitude of
is small comparatively to the magnitude of![]() , i.e.
, i.e.
![]() as expected. As a result,
as expected. As a result, ![]() function will be less useful in many cases. We can also ob-
function will be less useful in many cases. We can also ob-
serve that all curves are strictly monotonous. This tells us that, the strength of the DQ terms increase continously with time and no decoupling conditions occur in the BABA (with delta-pulse) and C7 pulse sequences.
5.4. BABA with Finite Pulse Width
Now, let us Consider, BABA pulse sequence with finite pulse width where the relation ![]() is valid during the interval where
is valid during the interval where ![]() acted (Figure 3) [55] [90] . We investigated the simplest case and considered
acted (Figure 3) [55] [90] . We investigated the simplest case and considered
only DQ terms in the function![]() . We generated two types of plots:
. We generated two types of plots: ![]() versus the dimensionless num-
versus the dimensionless num-
bers ![]() and
and ![]() as shown in Figure 3 (b) and Figure 4(b) in reference [55] . We studied the case,
as shown in Figure 3 (b) and Figure 4(b) in reference [55] . We studied the case, ![]() , corresponds to the spinning frequencies
, corresponds to the spinning frequencies![]() , and to the recoupling RF fields
, and to the recoupling RF fields![]() . In reference [55] , a closer look at Figure 3(b) (BABA with finite pulse widths) compared
. In reference [55] , a closer look at Figure 3(b) (BABA with finite pulse widths) compared
to BABA with delta-pulse width shows that the magnitude of the DQ terms of BABA with finite pulses is small
compared to the magnitude of BABA with ![]() sequences , i.e.
sequences , i.e.![]() , as expected [55] . In reference [55] , Figure 4(b) shows the plot of the function
, as expected [55] . In reference [55] , Figure 4(b) shows the plot of the function ![]() for versus the dimensionless number
for versus the dimensionless number
![]() , for the two cases:
, for the two cases: ![]() and
and ![]() . It can easily be seen that, when
. It can easily be seen that, when ![]() increases, the
increases, the
magnitude of the double quantum terms decreases, as expected. When![]() , the magnitude of the DQ term ®
, the magnitude of the DQ term ®
maximum corresponding to the delta-pulse sequence. However, when ![]() corresponding to
corresponding to ![]() , we have
, we have ![]() . The strength of the DQ terms decreases, cancel and build up again. This dynamic predicts that
. The strength of the DQ terms decreases, cancel and build up again. This dynamic predicts that
a full decoupling is possible, which occurs at![]() . The plot of the magnitude of the double quantum term of
. The plot of the magnitude of the double quantum term of![]() as a function of the pulse length gives a basic understanding of the experiment such as how to select robust finite pulse widths and how to select finite pulse widths that maximize or minimize double quantum terms. The study of this FME function could be helpful in predicting the conditions of decoupling.
as a function of the pulse length gives a basic understanding of the experiment such as how to select robust finite pulse widths and how to select finite pulse widths that maximize or minimize double quantum terms. The study of this FME function could be helpful in predicting the conditions of decoupling.
5.5. Criteria to Average out Chemical Shift Anisotropy for BABA
Application of the first contribution terms of the Floquet-Magnus expansion to the chemical shift anisotropy when irradiated with the BABA pulse sequence lead to an important condition for the CSA to be averaged out in each rotor period ![]() [53] [91] . Considering the CSA interactionin the following general form,
[53] [91] . Considering the CSA interactionin the following general form,
![]() , with
, with ![]()
![]() , we obtained the criterion for the CSA to be averaged out in each
, we obtained the criterion for the CSA to be averaged out in each ![]() period:
period: ![]() [91] . Similar criterion to average out CSA was obtained for BABA II (with
[91] . Similar criterion to average out CSA was obtained for BABA II (with![]() ),
), ![]() [91] . The coefficients
[91] . The coefficients ![]() depend on the orientation of the molecule and on the CSA tensor elements. The first order
depend on the orientation of the molecule and on the CSA tensor elements. The first order
of the argument of the propagator operator in FME approach was evaluated to
![]() (5)
(5)
A numerical analysis for a simple case consisting of one spin system with![]() ,
, ![]() evaluate instant
evaluate instant
neous values of the function![]() . These values are the magnitude of the CSA in different orientation of the
. These values are the magnitude of the CSA in different orientation of the
molecule and depend on the orientation of the molecule and on the CSA tensor elements. This complex function
can also be ploted versus the dimensionless number ![]() to get insight of the magnitude of the CSA in dif-
to get insight of the magnitude of the CSA in dif-
ferent orientation of the molecule.
6. Potential Approaches and Future Directions
Computing the exponential of a matrix is an important task in quantum mechanics and in nuclear magnetic resonance in particular where all theories used so far rely on exponential Hamiltonian operator propagators. The approximation of the matrix exponential is among the oldest and most extensive research topics in numerical mathematics [35] [39] [92] [93] . Although many efficient algorithms have been developed, so far, the problem is still not having being solved in general. Approaches such as scaling and squaring with Pade approximation, Chebyshev approximation, Krylov space methods, or splitting methods, have been used to approach the exponential of a matrix problem [39] . The main difficulty encountered in spectrum simulation is the rapid increase of computational requirements with an increasing number of spins. Simulation of spin system dynamics requires the numerical solution of the Liouville von Neumann equation, or equivalently the numerical exponential of a Liouville matrix [92] [93] . The Chebyshev approach has the potential to be extensively used in spin quantumdynamics and in particular NMR in the capacity of numerical simulations of spin physics of systems encounters. Our motivation of presenting the Chebyshev approximation as a potential surrogate of the popular expansions in NMR for the task of numerical simulations in spin dynamics paradigm stem from its numerical stability, high accuracy and also because its theoretical advantages are still not entirely realized for currently feasible computations [94] . I addition of the Chebyshev approximation, we introduce another alternative transformation called Cayley method that could be considered in some circumstances.
7. Chebyshev Approach
Nearly three decades ago, Tal-Ezer and Kosloff introduced the Chebyshev method as a means of solving the time-dependent Schrodinger equation in the field of molecular dynamics [37] [92] [94] . Tal-Ezer shown that the complex Chebyshev polynomials achieve the best approximation to expand the evolution operator. In the Chebyshev approach, the evolution operator ![]() is expended in a truncated series of Chebyshev polynomials. This procedure is applied by bounding the extreme eigenvalues
is expended in a truncated series of Chebyshev polynomials. This procedure is applied by bounding the extreme eigenvalues ![]() and
and ![]() of
of![]() . Then a trun
. Then a trun
cated Chebyshev expansion of ![]() on the interval
on the interval ![]() is considered where
is considered where![]() , with well-chosen coefficients
, with well-chosen coefficients ![]() [35] . The Chebyshev method has two main
[35] . The Chebyshev method has two main
advantages: first, it exploits the sparsity of the Liouvillian (Hamiltonian) by expressing the propagator in terms of a sequence of ![]() (Liouville superoperator) matrix multiples. Second, the Chebyshev expansion of the propagator is essentially exact. The series converges so rapidly that it is easily extended to the point where the truncation error is smaller than the usual round-off errors expected in any numerical computation [94] [95] . The method of Chebyshev approximation is frequently used in numerical quantum dynamics to compute
(Liouville superoperator) matrix multiples. Second, the Chebyshev expansion of the propagator is essentially exact. The series converges so rapidly that it is easily extended to the point where the truncation error is smaller than the usual round-off errors expected in any numerical computation [94] [95] . The method of Chebyshev approximation is frequently used in numerical quantum dynamics to compute ![]() over very long times. However, there are existing drawbacks in the Chebushev method. The scheme is not unitary, and therefore the norm is not conserved, but the deviation from unitarity is very small due to the extreme accuracy of the approach. Another drawback is that because of the long time durations of propagation in the Chebyshev scheme, intermediate results are not obtained.
over very long times. However, there are existing drawbacks in the Chebushev method. The scheme is not unitary, and therefore the norm is not conserved, but the deviation from unitarity is very small due to the extreme accuracy of the approach. Another drawback is that because of the long time durations of propagation in the Chebyshev scheme, intermediate results are not obtained.
8. Cayley Method
The Cayley transform provides a useful alternative to the exponential mapping relating the Lie algebra to the Lie group. This fact is particularly important for numerical methods where the evaluation of the exponential matrix is the most computation-intensive part of the algorithm [35] [97] . Blanes and co-workers shown that the solution
of Equation (1) can be written as ![]() with
with ![]() satisfying the dcayinv equation,
satisfying the dcayinv equation, ![]() and
and ![]()
![]() [41] - [44] .
[41] - [44] . ![]() is element of the Lie algebra
is element of the Lie algebra
such that if ![]() and
and ![]() are also elements of a Lie algebra which can be combined by the Lie bracket, which we represent by
are also elements of a Lie algebra which can be combined by the Lie bracket, which we represent by ![]() with the consideration of the orthogonal group, the Calyley transform is
with the consideration of the orthogonal group, the Calyley transform is
![]() . Note that the choice of
. Note that the choice of ![]() is arbitrary but it ensures, a particular simple form of
is arbitrary but it ensures, a particular simple form of
various expansion coefficients. Blanes and co-workers obtained the time-symmetric methods of order 4 and 6, based on the above Cayley transform where the efficiency of Cayley based methods can be built directly from Magnus based integrators [35] . But, unlike Magnus expansions, truncated Cayley expansions do not enjoy the benefits associated with time symmetry. As soon as integrals are replaced by appropriate quadrature formulas, Iserles proved that the time symmetry is gained [41] . The Cayley approach allows employing explicit schemes for solving the differential equation on the Lie algebra of the group and leads to semi-implicit methods where no iteration is required. The Caley methods in the numerical solution of matrix differential systems on quadratic groups have been applied to many important problems such as the Penrose regression problem (PRP) where this approach has been employed in finding numerical solution of PRP, the calculation of Lyapunov exponents of Hamiltonian systems, the solution of Hamiltonian isospectral problems, etc.... [41] -[44] [96] .
9. Conclusions
In this publication, we have thoroughly reviewed the abiding applications of average Hamiltonian theory, Floquet theory, and Floquet-Magnus expansion from very different perpectives in spin quantum physics of nuclear magnetic resonance. We also have presented some potential theories in NMR such as Fer expansion, Chebychev approximation, and possibly Cayley method. The combinations of two or more of the theories therein described will provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a way that can be easily extended to both synchronized and several non-synchronized modulations. We hope this publication will encourage the use of Floquet-Magnus and Fer expansions as numerical integrators as well as the use of Floquet-Magnus expansion as alternative approach in designing sophisticated pulse sequences and analyzing and understanding of different experiments. We also hope that this review will contribute to motivate spin dynamics experts in NMR to consider other perspectives and approaches beyond the scope of the current popular or used theories in the field of nuclear magnetic resonance. They are also many remarkable applications of the theory of NMR that we do not discuss in this review such as quantum information processing and computing. For example, the nuclear magnetic resonance quantum calculations of the Jones polynomial are interesting theoretical problems to tackle as well as theoretical treatment of problems with more than three frequencies analyzed using Floquet theory or Floquet-Magnus expansion approaches. In respect with the developments in the mathematical structure of AHT, FLT, FME, and FE, we expect that the realm of applications of the Floquet Magnus expansion and Fer expansion will also wide over the years. With new application in the field of NMR, we also expect the FME to generate new contributions like the generation of efficient numerical algorithm for geometric integrators.
The intention of writing this overview of theories and applications in nuclear magnetic resonance spectroscopy is to help bring the current and future prospective theoretical aspects of spin dynamics in NMR to the attention of the NMR community and lead new interactions between NMR experts and other specialists in mathematics, physics, chemistry, physical chemistry, and chemical physics. All these points strongly support the idea that the Floquet-Magnus expansion, the Fer expansion, the Chebyshev approach, and possibly the Cayley method can also be the very useful and powerful tools in quantum spin dynamics.
Acknowledgements
E. S. Mananga appreciates the moral supports of Profs. Joseph Malinsky, Andrew Akinmoladun and Akhil Lal, Mr. Hamad Khan and Mr. Alfred Romito.
NOTES
*Corresponding author.