Robust Adaptive Control for a Class of Systems with Deadzone Nonlinearity ()
1. Introduction
The significance of the deadzone problem lies in the fact that it affects many physical and practical systems. Examples of such systems are the ones containing hydraulic or pneumatic values, electronic circuits and devices, temperature regulation circuits, and in actuators such as servo valves and DC motors. In most cases, the pa- rameters of the deadzone nonlinearity are unknown and continuously varying with time and temperature. Deadzones exist in a number of industrial applications specially the ones requiring high precision such as medical robots, semiconductor manufacturing, and precision machine tools. It has been shown that deadzone in actuators, such as hydraulic servo-valves, gives rise to limit cycling and instability. The advances reached in the area of adaptive compensation and control theory gave rise to increased interest in handling the deadzone problem. There have been many techniques that addressed the problem and have been shown to reduce if not eliminate the degradation of system performance resulting in an improved tracking accuracy and ensured stabilization of such systems.
One sensible approach to counter the effect of the deadzone, shown in Figure 1, was presented by [1] which involved designing an inverse deadzone function to cancel its effect. The approach of designing an inverse adaptive deadzone compensator was thoroughly investigated in [2] and [3] which was shown to improve per- formance. Lewis et al. in [4] proposed a fuzzy logic type inverse deadzone compensator, meanwhile, a neural network inverse compensator was designed in [5] . Both approaches show clear improvement in reducing the tracking error. In [6] , a new adaptive controller of linear or nonlinear systems with deadzone is introduced with- out constructing a deadzone inverse. Global and asymptotic tracking was achieved and simulation results were presented.
An adaptive sliding mode control scheme used to offset a non-symmetrical deadzone nonlinearity in continu- ous time was presented in [7] . The problem of chattering inherent with sliding mode control is handled by al- lowing a small controlled tracking error.
In recent years, many researchers addressed the deadzone problem with encouraging results. In [8] , a novel function was introduced to describe deadzone nonlinearity. To show the effectiveness of the proposed equivalent function the authors combined it with vibration of a cantilever beam.
In this paper we are motivated by the success of our earlier results deadzone compensation of DC motor pre- sented in [9] and [10] . The extension involves combining the deadzone for a class of linear systems with uncer- tainties in the span of the input. The uncertainties are assumed to be bounded by a pth order polynomial in the state of the system. A robust adaptive controller will compensate for the unmeasurable disturbances as well as any mismatch error in estimating the deadzone parameters. The proposed method does not require any know- ledge of the deadzone parameters or the specialized design of an inverse deadzone controller and only an upper bound of the deadzone spacing which is easily determined a priori.
2. The Problem Setup: Dynamics of a Non-Symmetrical Deadzone Nonlinearity
A common representation of a non-symmetrical deadzone nonlinearity, shown in Figure 1, described in [1] as follows
 (1)
(1)
where  denotes the output of deadzone function preceding a plant input,
denotes the output of deadzone function preceding a plant input,  is the slope of the lines,
is the slope of the lines,  is the width of the deadzone distance, and
is the width of the deadzone distance, and  is the input of the deadzone block as shown in Figure 1. A more convenient representation of a non-symmetrical deadzone was presented in [6] as
is the input of the deadzone block as shown in Figure 1. A more convenient representation of a non-symmetrical deadzone was presented in [6] as
 (2)
(2)
where  represents a non-symmetrical saturation function given by
represents a non-symmetrical saturation function given by
![]()
Figure 1. Non-symmetric deadzone nonlinearity at the input of a linear plant.
 (3)
(3)
A novel representation for (2) was presented in [11] for an exact symmetrical deadzone by defining  as the deadzone spacing function as
as the deadzone spacing function as
 (4)
(4)
Consequently, the saturation function can be written as
 (5)
(5)
In most applications the deadzone parameters are unknown or time and temperature varying. Instead, for de- veloping an inverse deadzone function as in [9] , we advocate a robust adaptive compensator that handles the variability of the deadzone parameters as part of an input disturbance. However, we outline some necessary and reasonable assumptions to be used in the proof of the efficacy of the proposed control methodology:
(A1) The deadzone parameters  and
and .
.
(A2) The deadzone parameters , and
, and 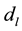 are bounded as follows:
are bounded as follows:
![]() and.
and.
(A3) Without any loss of generality, the slope of the deadzone ![]() is positive and is set to 1.
is positive and is set to 1.
(A4) The output of the deadzone block ![]() is not available for measurement.
is not available for measurement.
Remark 1. Assumptions (A1) and (A2) are the actual physical attributes of a real industrial deadzone and is adopted in the literature [6] . Therefore, the saturation function given by (4) can be shown to have an upper bound by closely analysing Equation (5). Using the general inequality rule ![]() we have
we have
![]() (6)
(6)
![]() (7)
(7)
From Equations (6) from (7) we can state
![]() (8)
(8)
Multiplying by the slope ![]() gives
gives
![]() (9)
(9)
The left hand side of (9) is the saturation function given by (5). In case of a non-symmetrical deadzone func- tion the upper-bound may be chosen by employing assumption (A2) as follows
![]() (10)
(10)
where
![]() (11)
(11)
The upper bounds will play a pivotal role to ensure the overall global stability of the close loop dynamics as will be demonstrated in the following section.
3. Robust Adaptive Controller Design
Considering the following nonlinear system with input deadzone nonlinearity described as
![]() (12)
(12)
where the matrices ![]() and
and ![]() are given by
are given by
![]()
And ![]() represents the unmeasurable disturbance. The collective bounds can be expressed as
represents the unmeasurable disturbance. The collective bounds can be expressed as
![]() (13)
(13)
Let the reference model to be tracked given by
![]() (14)
(14)
where ![]() and
and ![]() is a reference signal. The tracking error dynamics
is a reference signal. The tracking error dynamics ![]() may be written as fol- lows:
may be written as fol- lows:
![]() (15)
(15)
Inserting the deadzone equation (2) into (15) yields
![]() (16)
(16)
Therefore, for the class of systems described in (13) and deadzone given in (7), we use the result stated as Lemma RANDM in [12] and modify it to ensure asymptotic convergence. The modified controller is
![]() (17)
(17)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is the positive definite symmetric solution of the Algebraic Riccati equation (ARE). The adaptation
is the positive definite symmetric solution of the Algebraic Riccati equation (ARE). The adaptation ![]() is used to ensure robustness of the controller. The combined output of the com- pensator and the deadzone nonlinearity may be written as
is used to ensure robustness of the controller. The combined output of the com- pensator and the deadzone nonlinearity may be written as
![]() (18)
(18)
Inserting the proposed control laws (17) and the output of the deadzone block given by Equation (18) into the error dynamics (16) results in the closed loop dynamics
![]() (19)
(19)
The adaptation law for ![]() given by
given by
![]() (20)
(20)
where ![]() is a constant scalar.
is a constant scalar.
Theorem. For the plant described by (12) with input deadzone (1), and the robust adaptive control law (17) along with the adaptive update law (20) will ensure the closed-loop stability and boundedness of tracking error, hence reducing the effects of deadzone.
Proof. Using the following positive definite control Lyapunov function
![]() (21)
(21)
where ![]() differentiating along the trajectories of the system yields
differentiating along the trajectories of the system yields
![]() (22)
(22)
![]() (23)
(23)
Substituting for the closed loop dynamics given by (19) in (23) gives
![]() (24)
(24)
Collecting terms and simplifying
![]() (25)
(25)
Rearranging terms we get
![]() (26)
(26)
The first term can be simplified by solving the Algebraic Reccati Equation given by
![]() (27)
(27)
resulting in
![]() (28)
(28)
Replacing the adaptation law (20) and replacing ![]() in (28) yields
in (28) yields
![]() (29)
(29)
![]() (30)
(30)
So far the first two terms are negative. As for the third term we utilize the general inequality ![]() to establish proper bounds as follows
to establish proper bounds as follows
![]() (31)
(31)
Using the inequality (13) to modify (31) to become
![]() (32)
(32)
Therefore, the inequality of (32) can be incorporated in (30) as
![]() (33)
(33)
By choosing the degree of freedom ![]() satisfying the condition
satisfying the condition ![]() and choosing
and choosing ![]() to be great-
to be great-
er than ![]() ensures that the first three terms of
ensures that the first three terms of ![]() negative. Meanwhile, the last term in (33) can be upper bounded as follow
negative. Meanwhile, the last term in (33) can be upper bounded as follow
![]() (34)
(34)
Utilizing the upper bounds on ![]() given by (10) and rewriting the right hand side of (34)
given by (10) and rewriting the right hand side of (34)
![]() (35)
(35)
where![]() .Therefore the last term in (35) insures that
.Therefore the last term in (35) insures that ![]() as long as
as long as
![]() (36)
(36)
or
![]() (37)
(37)
To conclude, by choosing ![]() then
then ![]() is rendered negative and
is rendered negative and ![]() converges to a closed and vanishing region as time increases. Therefore, since
converges to a closed and vanishing region as time increases. Therefore, since ![]() as
as ![]() and
and ![]()
implies that by choosing the ![]() vector as the coefficient of a strictly Hurwitz polynomial will make the closed loop system error asymptotically stable. For a more through conclusion of the proof one may refer to [13] .
vector as the coefficient of a strictly Hurwitz polynomial will make the closed loop system error asymptotically stable. For a more through conclusion of the proof one may refer to [13] .
4. Illustrative Example
In this section, we illustrate the proposed controller to compensate for a system with a deadzone nonlinearity presented in [14] as
![]() (38)
(38)
The parameter used for the simulation is shown in Table 1. The plant (41) may be written in state space form by defining ![]() and
and ![]() then
then
![]() (39)
(39)
![]()
Resulting in
![]()
The solution of the ARE equation was chosen to be
![]()
![]()
Table 1. Parameters utilized in the example.
The reference model to be tracked is
![]()
for a sinusoidal reference trajectory given by
![]()
Meanwhile, the unmeasurable disturbance ![]() can be collectively bounded as
can be collectively bounded as
![]() (40)
(40)
Simulations of the system in (39) under the adaptive control law (17) and (20) have been performed. The up- per bounds on actuator actual spacing ![]() is assumed unknown. In order to demonstrate the performance improvement accomplished by our proposed method, the system under test given in (39) was used. The efficacy of the proposed method is proven by comparing its performance against the performance of a clas- sic PD controller having equivalent gains. The complete parameters of the system under test and controller gains are listed in Table 1.
is assumed unknown. In order to demonstrate the performance improvement accomplished by our proposed method, the system under test given in (39) was used. The efficacy of the proposed method is proven by comparing its performance against the performance of a clas- sic PD controller having equivalent gains. The complete parameters of the system under test and controller gains are listed in Table 1.
The simulation results presented in Figure 2 and Figure 3, clearly show the tracking performance for ![]() and
and ![]() states along with their respective reference trajectory. Figure 4 and Figure 5 demonstrate the tracking error for the states
states along with their respective reference trajectory. Figure 4 and Figure 5 demonstrate the tracking error for the states ![]() and
and ![]() in blue in addition to the same tracking errors for the system under a PD con- troller in red. In both figures, the PD controller resulted in limit cycles where as the adaptive controller proved to be stable with no limit cycles and improved performance with a zero approaching tracking error. Figure 6 shows the control effort
in blue in addition to the same tracking errors for the system under a PD con- troller in red. In both figures, the PD controller resulted in limit cycles where as the adaptive controller proved to be stable with no limit cycles and improved performance with a zero approaching tracking error. Figure 6 shows the control effort ![]() and
and![]() . In Figure 7 the evolution of the
. In Figure 7 the evolution of the ![]() which clearly demonstrates the boundedness of the adaptation. In Figure 8, the reference trajectory is changed to demonstrates a superior a step response performance when compared with PD controller. While the step error is approaching zero for the system under the proposed adaptive controller, a steady state error is persistent with the PD controller.
which clearly demonstrates the boundedness of the adaptation. In Figure 8, the reference trajectory is changed to demonstrates a superior a step response performance when compared with PD controller. While the step error is approaching zero for the system under the proposed adaptive controller, a steady state error is persistent with the PD controller.
![]()
Figure 2. The tracking performance of ![]() state of the system under the proposed robust controller.
state of the system under the proposed robust controller.
![]()
Figure 3. The tracking performance of ![]() state of the system.
state of the system.
![]()
Figure 4. The adaptively compensated tracking error ![]() (blue) vs. the same tracking error of the system under a PD controller (red).
(blue) vs. the same tracking error of the system under a PD controller (red).
![]()
Figure 5. The adaptively compensated tracking error ![]() (blue) vs. the same tracking error of the system under a PD controller (red).
(blue) vs. the same tracking error of the system under a PD controller (red).
![]()
Figure 6. The control effort ![]() in red vs.
in red vs. ![]() for the deadzone compensated system.
for the deadzone compensated system.
![]()
Figure 8. Step tracking performance error for ![]() for input
for input![]() .
.
5. Conclusion
A robust adaptive controller is used to control a class of nonlinear systems with input deadzone nonlinearity at the input. The robust controller was shown to be superior in performance when compared to a more conventional control method such as a PD controller. The system under the proposed scheme has been shown to not only ef- fectively stabilize a second order complex nonlinear system with disturbance, but also achieve asymptotic tracking. The advantage of the proposed method lies in the fact that no knowledge of the deadzone parameters needed and only an upper bound for the deadzone spacing is required. The adaptive deadzone inverse controller is smoothly differentiable and can easily be combined with any of the advanced control methodologies. The asymptotic stability of the closed-loop system has been proven by using Lyapunov arguments and simulation results confirmed the efficacy of the control methodology.
Funding
This work is supported and funded by the Public Authority of Applied Education and Training, Research Project No. (TS-14-03) t, Research Title (Adaptive Control of Systems with Output Deadzone).
NOTES
*Corresponding author.