Encrypted Sensing Based on Digital Holography for Fingerprint Images ()
1. Introduction
Recently, there has been a rise in the use of biometric authentication systems in a wide variety of secure interfaces, including computer logins, banking systems, automated teller machines, and building entrance management. Because biometric information represents important personal data, and because enrolled biometric information, unlike most personal authentication information such as passwords, cannot be altered, it is necessary to take great care to prevent leakage of these data. Correspondingly, template protection techniques for biometric authentication have been actively pursued through the development of cryptographic algorithms that protect raw biometric information obtained using a sensor while preserving high verification accuracy [1] -[4] . However, particular threats, such as side-channel attacks [5] occurring while raw biometric information is being transformed into a protected template, are becoming increasingly realistic. It is believed that threats such as these can be avoided by encrypting biometric images prior to image sensing, i.e., optical en- cryption.
Optical encryption techniques apply optical calculation methods such as optical wave propagation oroptical phase modulation for image encryption and decryption. These techniques are advantageous not only for rapid calculations using parallel processing, but also security enhancement due to non-electronic computation methods, because there is less risk of optical information being read, as opposed to digital data in electronic devices, which are inevitably exposed to a number of security risks. Double random phase encoding (DRPE) [6] is a well-known optical encryption method that has been studied extensively for two decades. DRPE is an optical symmetric-key encryption technique in which an optical image is encrypted by multiplying two random phase masks in the spatial and Fourier or Fresnel planes. To obtain an optically-encrypted image, digital holography (DH) [7] -[10] is commonly employed. DH makes it possible to not only capture an optical wavefront as holo- graphic data, but also to reconstruct various styles of optical wavefront computationally from the holographic data. DRPE has been implemented using DH [7] [11] , whereby the random phase masks are typically inserted into the object beam path. Suchan optical system requires precise alignment; however, it is challenging to reconstruct the object image with high quality from the DH. Tajahuerce and Javidi proposed an optical encryption system for three-dimensional (3D) objects [12] , whereby an encrypted image was obtained with simple alignment because only the reference beam was modulated using a random phase mask, and a non-modulated wave was used as the object beam. This optical arrangement could be implemented easily and can restore a clear object image from a DH. However, the encrypted image was not equivalent to DRPE because the object beam was not modulated by a random phase mask, which might decrease the security level of encryption. To obtain a fingerprint image for biometric authentication, both sufficient security to prevent data leakage and sufficient image quality for highly accurate recognition are required. Therefore, we propose an optical security system that is suitable for obtaining fingerprint images as optically encrypted holographic data. We term this system “encrypted sensing”. In addition, we also propose an image reconstruction method through which we can obtain a clear fingerprint image from the encrypted hologram. To obtain the reconstructed image with high quality, we apply speckle reduction using multiple holograms, as well as reconstruction using a phase only mask, rather than a complex amplitude mask. We demonstrate that improved recognition accuracy is obtained by applying only a phase-only mask and speckle reduction.
The remainder of the paper is organized as follows. In the following section, a theoretical description of the proposed sensing system is given. In Section 3, experiments for obtaining encrypted fingerprint images are de- scribed, together with an investigation of the quality of the decrypted fingerprint images. Conclusions are drawn in Section 4.
2. Method
2.1. User Authentication Scheme
Figure 1 shows a schematic diagram that illustrates the concept of biometric encrypted sensing proposed here. During enrollment, biometric information (i.e., a fingerprint pattern) is encrypted using the optical system within the biometric sensor, and the encrypted information is transmitted to the verification system for user authentica- tion. This encrypted biometric information is then decrypted using a corresponding decryption key and the bio- metric information is stored in the biometric template database. During verification, encrypted biometric infor- mation is also captured, and it is then sent to the verification system. Subsequently, it is also decrypted in the ve- rification system, and the biometric information and the enrolled data are verified by calculating their similarity. If both the biometric image and the encryption key are provided correctly, the user is authorized. This system makes it possible to perform two-factor authentication that will authorize users only when both biometric and the secret data are verified. The verification system, which is assumed to be a securely protected using, for ex- ample, a tamper-resistant device can be located in either a centralized server or a user device. Throughout this overall process, raw biometric information in digital form exists only in the protected verification system, and the risk of theft or leakage of biometric data is thus significantly reduced.
2.2. Encrypted Sensing Based on DRPE
In our system, optical encryption is performed via a combination of DH and DRPE. With DH, a wavefront encoding the optical information from an object wave is typically captured via interference with a reference plane wave, as shown in Figure 2. In ref. [12] , random phase-modulated light was used as the reference wave, which is used as an encryption key. In our system, both the object wave and the reference wave are modulated using diffusers, as shown in Figure 3. To capture fingerprints stably, we place a total reflection prism in the middle of the object wavepath. The resulting DH is captured using a charged coupled device (CCD) image sensor, and can be expressed as follows:
 (1)
(1)
where  represents the fingerprint image,
represents the fingerprint image,  is the phase modulation by the diffuser in the object wavepath,
is the phase modulation by the diffuser in the object wavepath, 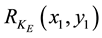 is the complex amplitude distribution of the phase-modulated reference wave on the CCD plane,
is the complex amplitude distribution of the phase-modulated reference wave on the CCD plane, 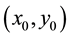 and
and 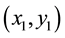 are coordinates of the object and the CCD planes, and * denotes the complex conjugate. The operator
are coordinates of the object and the CCD planes, and * denotes the complex conjugate. The operator  denotes a Fresnel transform in which f and z are the original wavefront and the propagation distance, respectively.
denotes a Fresnel transform in which f and z are the original wavefront and the propagation distance, respectively.  is derived as the Fresnel transform of the phase object assigned by the diffuser D2 (see Figure 3).
is derived as the Fresnel transform of the phase object assigned by the diffuser D2 (see Figure 3).
Figure 4 shows a flow chart of the Fresnel-type DRPE process. An encrypted image is obtained via two phase modulations―one in the space domain, and the other in the Fresnel domain. With the approaches described in Refs. [7] and [11] , two phase masks were inserted in the object wave path for DRPE; however, with our system,
![]()
Figure 1. Concept of the encrypted biometric sensing system. The database (DB) in the verification system represents the template database for user biometric information.
![]()
Figure 2. Typical optical system used in digital holography.
![]()
Figure 3. The optical system used with our encrypted sensing scheme. Here D1 and D2 are diffusers.
![]()
Figure 4. Schematic diagram illustrating the Fresnel-type DRPE scheme.
they are applied to the object and reference waves. The Fresnel-type DRPE uses three cipher keys: the phase distribution on the Fresnel domain, the distance of Fresnel diffraction, and the wavelength of laser; all of which that must be provided correctly to restore the plaintext image from the encrypted image. In this paper, the laser wavelength is assumed to be unique, whereas the other two components are employed as cipher keys.
Let us consider the third term of Equation (1), which is similar to DRPE. If the amplitude of 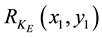 can be approximated to be constant, the third term of Equation (1) corresponds to the encrypted image of Fresnel-type DRPE. In this case,
can be approximated to be constant, the third term of Equation (1) corresponds to the encrypted image of Fresnel-type DRPE. In this case,  can be expressed as
can be expressed as
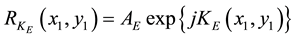 (2)
(2)
where AE is a constant amplitude and 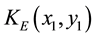 is the phase distribution of the encryption key. The encrypted image
is the phase distribution of the encryption key. The encrypted image ![]() is then given by
is then given by
![]() (3)
(3)
where the constant AE has been omitted for clarity. The encrypted image ![]() can be derived by reconstructing the first-order diffracted wave from the digital hologram captured by the CCD sensor.
can be derived by reconstructing the first-order diffracted wave from the digital hologram captured by the CCD sensor.
For decryption, ![]() is multiplied by the phase term of the decryption key image
is multiplied by the phase term of the decryption key image ![]() as follows:
as follows:
![]() (4)
(4)
After this calculation, the complex amplitude image ![]() is Fresnel-diffracted at a distance
is Fresnel-diffracted at a distance![]() , and a decrypted image
, and a decrypted image ![]() is obtained by calculating its amplitude components as follows:
is obtained by calculating its amplitude components as follows:
![]() (5)
(5)
where ![]() are coordinates on the new Fresnel transform domain. If the encryption key
are coordinates on the new Fresnel transform domain. If the encryption key ![]() and the decryption key
and the decryption key ![]() are identical or very similar,
are identical or very similar, ![]() becomes as follows:
becomes as follows:
![]() (6)
(6)
If![]() , this yields the following:
, this yields the following:
![]() (7)
(7)
From this equation, it follows that the original fingerprint image is obtained.
If the amplitude of ![]() cannot be approximated to be constant, the complex amplitude of
cannot be approximated to be constant, the complex amplitude of ![]() must be obtained, which entails division process by its amplitude component in the decryption process, as described in Ref. [12] . This process can lead to amplification of the error of a restored fingerprint image, because some pixels of the amplitude component of
must be obtained, which entails division process by its amplitude component in the decryption process, as described in Ref. [12] . This process can lead to amplification of the error of a restored fingerprint image, because some pixels of the amplitude component of ![]() may be very small. In our experimental analysis below, we investigate both cases in which
may be very small. In our experimental analysis below, we investigate both cases in which ![]() has either a constant amplitude (our method) or a complex amplitude distribution (similar to Tajahuerce’s method).
has either a constant amplitude (our method) or a complex amplitude distribution (similar to Tajahuerce’s method).
If the encryption and decryption keys differ significantly, the decrypted image becomes a random pattern. The diffraction distance z can be also used as a parameter to restore the correct plaintext image.
2.3. Obtaining the Decoding Key
To implement a recording system for encrypted DH, we employ off-axis holography, in contrast to the work described in Ref. [12] , where they used in-line holography. To reconstruct a fingerprint image from an encrypted hologram, ![]() must be obtained in advance. To implement this with off-axis holography, a Fourier transform-based method [13] was employed.
must be obtained in advance. To implement this with off-axis holography, a Fourier transform-based method [13] was employed.
In the optical system shown in Figure 5, a hologram ![]() is obtained via interference between
is obtained via interference between ![]() and a plane wave, i.e.,
and a plane wave, i.e.,
![]() (8)
(8)
Where ![]() is a unit-amplitude plane wave, where a and b represent the angles between
is a unit-amplitude plane wave, where a and b represent the angles between ![]() and the plane wave. To eliminate the first and second terms of Equation (8), the intensity distribution of
and the plane wave. To eliminate the first and second terms of Equation (8), the intensity distribution of ![]() is recorded by shielding the plane wave, and
is recorded by shielding the plane wave, and ![]() (which is constant) and
(which is constant) and ![]() are numerically subtracted from
are numerically subtracted from![]() . Subsequently, the remaining terms are Fourier-transformed and we have
. Subsequently, the remaining terms are Fourier-transformed and we have
![]() (9)
(9)
where ![]() are coordinates on the Fourier domain,
are coordinates on the Fourier domain, ![]() is the Fourier transform of
is the Fourier transform of![]() , and Ä denotes a convolution operator. If a and b are large enough to separate the two terms in Equation (9) in the spectral domain, the first and second terms do not overlap, and the first term can be extracted by shielding the second term. By calculating the inverse Fourier-transform, the complex amplitude distribution of
, and Ä denotes a convolution operator. If a and b are large enough to separate the two terms in Equation (9) in the spectral domain, the first and second terms do not overlap, and the first term can be extracted by shielding the second term. By calculating the inverse Fourier-transform, the complex amplitude distribution of ![]() can be determined.
can be determined.
3. Experiments
3.1. Optical System
We carried out several experiments in which holograms of encrypted fingerprint images were captured and the original fingerprint images were then numerically restored. To do this, we constructed an optical system for acquiring holograms, as shown in Figure 6, which used a He-Ne laser with a wavelength of 633 nm as a light source and a CCD image sensor with 1024 × 768 pixels that was 4.65 μm ´ 4.65 μm. A fingerprint was placed on a total reflection prism and the reflected light was focused using two lenses (L3 and L4) to form an image on the CCD image sensor.
3.2. Image Reconstruction
As discussed in Section 2.2, the decrypted images were obtained so that ![]() was either treated as a complex amplitude wave (as with Tajahuerce’s method) or with the amplitude component replaced with a constant value (our method). Examples of an encrypted hologram
was either treated as a complex amplitude wave (as with Tajahuerce’s method) or with the amplitude component replaced with a constant value (our method). Examples of an encrypted hologram ![]() and the corresponding decrypted images are shown in Figure 7. Figure 7(a) shows that the fingerprint image is not visible in the encrypted hologram
and the corresponding decrypted images are shown in Figure 7. Figure 7(a) shows that the fingerprint image is not visible in the encrypted hologram![]() . Figure 7(b) shows adecrypted image using the correct
. Figure 7(b) shows adecrypted image using the correct ![]() with a complex amplitude
with a complex amplitude
![]()
Figure 5. Optical system for obtaining decoding key.
![]()
Figure 6. Schematic diagram showing the experimental optical system. Here f1 = 0.2 m, f2 = 0.1 m, d1 = 0.056 m, and d2 = 0.2 m.
component and the correct propagation distance. In this case, the fingerprint image is difficult to discern. Figure 7 (c) shows a decrypted image using the correct ![]() with a constant amplitude and the correct propagation distance; the fingerprint pattern can be clearly seen in the decrypted image. These results indicate that better quality fingerprints can be obtained by using a constant amplitude for
with a constant amplitude and the correct propagation distance; the fingerprint pattern can be clearly seen in the decrypted image. These results indicate that better quality fingerprints can be obtained by using a constant amplitude for ![]() than by using a complex amplitude. However, the fingerprint pattern in Figure 7(c) contains significant speckle noise [14] [15] , although it is sufficiently clear to recognize using the human eye. To reduce the amount of noise, we captured multiple holograms with differing speckle noise by changing the position of diffuser D1on the object beam path and summing the intensities of the decrypted images obtained from the holograms. Figure 7(d) shows a decrypted image obtained by summing four decrypted images, in which the restored fingerprint is more clearly visible than in Figure 7(c).
than by using a complex amplitude. However, the fingerprint pattern in Figure 7(c) contains significant speckle noise [14] [15] , although it is sufficiently clear to recognize using the human eye. To reduce the amount of noise, we captured multiple holograms with differing speckle noise by changing the position of diffuser D1on the object beam path and summing the intensities of the decrypted images obtained from the holograms. Figure 7(d) shows a decrypted image obtained by summing four decrypted images, in which the restored fingerprint is more clearly visible than in Figure 7(c).
Figures 7(e) shows a decrypted image using an incorrect![]() , and Figure 7(f) shows a decrypted image using an incorrect propagation distance. In both cases, random patterns similar to stationary white noise were obtained.
, and Figure 7(f) shows a decrypted image using an incorrect propagation distance. In both cases, random patterns similar to stationary white noise were obtained.
3.3. Verification Accuracy
We evaluated the verification accuracy of the experimental setup described above in terms of the ability to match restored fingerprint images. Using the optical system shown in Figure 6, we captured 100 encrypted holograms of fingerprint images from 10 subjects (10 encrypted DHs per fingerprint). In these trials, five of the fingerprint images for each subject were used for enrollment and the others were used for testing; 250 genuine fingerprint trials (25 trials per subject) and 450 imposter trials (45 trials per subject) were carried out. Nonlinear correlation [16] was employed in these trials for pattern matching. The nonlinear correlation n(x,y) between two images can be expressed as follows:
![]() (10)
(10)
Where ![]() (m = 1, 2) denotes the Fourier transform of each image, IFT denotes inverse Fourier transform operator,
(m = 1, 2) denotes the Fourier transform of each image, IFT denotes inverse Fourier transform operator, ![]() is the phase distribution of
is the phase distribution of ![]() and k is the degree of the applied nonlinearity. We choose k = 0.3, which was found to provide optimal discrimination between genuine and imposter cases. Figure 8 shows the nonlinear correlation output; the correlation waveforms exhibited a sharp peak when verifying the correct fingerprint (a genuine case) with a constant amplitude
and k is the degree of the applied nonlinearity. We choose k = 0.3, which was found to provide optimal discrimination between genuine and imposter cases. Figure 8 shows the nonlinear correlation output; the correlation waveforms exhibited a sharp peak when verifying the correct fingerprint (a genuine case) with a constant amplitude![]() , and with speckle noise reduction, the correlation peak became sharper. Figure 8(d) shows nonlinear correlation in case of verification between a correct and an incorrect decryption keys. Although both decrypted images were obtained from the same encrypted hologram, the nonlinear correlation did not exhibit a peak. Figure 8(e) shows the correlation waveform for imposter verification; here we also see a random pattern.
, and with speckle noise reduction, the correlation peak became sharper. Figure 8(d) shows nonlinear correlation in case of verification between a correct and an incorrect decryption keys. Although both decrypted images were obtained from the same encrypted hologram, the nonlinear correlation did not exhibit a peak. Figure 8(e) shows the correlation waveform for imposter verification; here we also see a random pattern.
As a quantitative criterion for verification, the peak-to-side-lobe ratio (PSR) [17] was calculated as follows:
![]() (11)
(11)
where σ denotes the standard deviation of ![]() and peak and mean denote the peak value and spatial average of
and peak and mean denote the peak value and spatial average of![]() , respectively.
, respectively.
Using PSR as a verification score, the false rejection rate (FRR) of the genuine verification attempts and the false acceptance rate (FAR) of the imposter verification attempts were calculated. In addition, we determined a receiver operating characteristic (ROC) curve, in which each point is plotted according to the FRR (x-axis) and FAR (y-axis) for a given threshold value, as shown in Figure 9. The equal error rate (EER) of our method with speckle noise reduction was 12.4%, and that without speckle noise reduction was 35.0%. The EER obtained using a complex amplitude ![]() was 45.0%. These results indicate that the phase-only method proposed here provides better image verification, and that the speckle noise reduction contributes significantly to the improvement in the verification accuracy.
was 45.0%. These results indicate that the phase-only method proposed here provides better image verification, and that the speckle noise reduction contributes significantly to the improvement in the verification accuracy.
The accuracy of our system was not better than that of image verification using a conventional sensor (i.e., unencrypted sensing). However, there are a number of possible causes of image degradation: first, we did not use a guide to fix the fingerprints; and second, we did not ask the subjects to restrain the pressure that they applied. The latter issue might cause a variation in the degree of fingerprint distortion among the images. In such cases, speckle reduction via summation may not be effective. By reducing the influence of such factors, our method has potential for further improvements in verification accuracy.
4. Conclusions
We have described an encrypted sensing system for capturing fingerprint images using digital holography and
optical encryption. We showed experimentally that a fingerprint image could be restored correctly by decrypting an encrypted hologram with the correct key and propagation distance. The quality of the restored fingerprint im- age could be more clearly visible than that when using a conventional method by improving the calculation method for restoring a fingerprint image from an encrypted digital hologram. The verification performance of the restored fingerprint images was investigated, and we demonstrated that our method has favorable verification accuracy.
The principal advantage of the system described here is that it can enhance the security of biometric authentication by capturing optically encrypted images rather than raw fingerprints. Combining physically unclonable functions (PUFs) [18] with our system might enable the development of very secure user authentication methods. For example, the use of an encoding key provided by a diffuser as a PUF may provide a secure key based on the physical features of an individual object.
NOTES
*Corresponding author.