Evaluation of Kinetic Properties of Dendritic Potassium Current in Ghostbursting Model of Electrosensory Neurons ()
1. Introduction
Hodgkin and Huxley [1] proposed a mathematical model that is composed of a system of four-coupled nonlinear ordinary differential equations (page 518 in [1] ) and that describes the action potential regeneration of the squid giant axon and the biophysical mechanisms underlying the action potential generation. Various types of mathematical models describing the electrical excitability of neurons and endocrine cells have been developed on the basis of the concepts proposed by Hodgkin and Huxley [1] , and analyses of these models, including the RPeD1 neuron model in [2] , various bursting models in Chapter 5 of [3] , and pituitary lactotroph bursting model in [4] , are important research areas in the field of applied mathematics. The concepts proposed by Hodgkin and Huxley [1] are also important in the fields of theoretical physics [5] and mathematical physics [6] . The Hodgkin-Huxley model is also used in drug-disease modeling (see Chapter 5.2.2 in [7] ).
A ghostbursting model [8] , which is a mathematical model based on the concepts proposed by Hodgkin and Huxley [1] , describes a system of six-coupled nonlinear ordinary differential equations [see Equations (1) to (6) in Section 2]. This model exhibits bursting similar to that observed in in vitro recordings of pyramidal cells in the electrosensory lateral line lobe (ELL) of the weakly electric fish Apteronotus leptorhynchus. This model consists of two compartments: the somatic compartment [see Equations (1) and (2) in Section 2] and the dendritic compartment [see Equations (3) to (6) in Section 2]. Doiron et al. have focused on two system parameters of the model: maximal conductance of the delayed-rectifying potassium current in the dendritic compartment 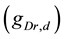 [see Equation (3)] and the current injected into the somatic compartment
[see Equation (3)] and the current injected into the somatic compartment 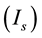 [see Equation (1)]. They performed
[see Equation (1)]. They performed 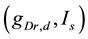 -parameter bifurcation analysis of the model (see Figure 6 in [8] ). This figure indicates that the organizing center of the
-parameter bifurcation analysis of the model (see Figure 6 in [8] ). This figure indicates that the organizing center of the 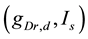 -parameter bifurcation diagram is a codimension-two bifurcation point and that unfolding the codimension-two bifurcation point yields two types of bifurcation manifolds: a curve for a saddle-node bifurcation of fixed points (SNFP curve) and a curve for a saddle-node bifurcation of limit cycles (SNLC curve). The SNFP and SNLC curves divide the
-parameter bifurcation diagram is a codimension-two bifurcation point and that unfolding the codimension-two bifurcation point yields two types of bifurcation manifolds: a curve for a saddle-node bifurcation of fixed points (SNFP curve) and a curve for a saddle-node bifurcation of limit cycles (SNLC curve). The SNFP and SNLC curves divide the 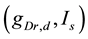 -parameter space into three dynamical states: quiescence, periodic tonic spiking, and bursting. When crossing the SNFP curve with an increase in
-parameter space into three dynamical states: quiescence, periodic tonic spiking, and bursting. When crossing the SNFP curve with an increase in 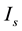 under a condition in which
under a condition in which 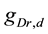 is fixed to a certain value smaller than the
is fixed to a certain value smaller than the 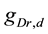 value at the codimension-two bifurcation point, the dynamical state changes from quiescence to bursting. When crossing the SNFP curve with an increase in
value at the codimension-two bifurcation point, the dynamical state changes from quiescence to bursting. When crossing the SNFP curve with an increase in 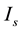 under a condition in which
under a condition in which 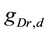 is fixed to a certain value larger than the
is fixed to a certain value larger than the ![]() value at the codimension-two bifurcation point, the dynamical state changes from quiescence to periodic tonic spiking. The periodic tonic spiking further changes into bursting when the SNLC curve is crossed with an increase in
value at the codimension-two bifurcation point, the dynamical state changes from quiescence to periodic tonic spiking. The periodic tonic spiking further changes into bursting when the SNLC curve is crossed with an increase in![]() . In addition, various bursting patterns are shown in Figure 13 in [8] and Figure 3 in [9] .
. In addition, various bursting patterns are shown in Figure 13 in [8] and Figure 3 in [9] .
Vo et al. have indicated that it is important to investigate the kinetic properties of ionic conductance for understanding the dynamics of pituitary cell models [10] . In other words, variations in the time constant values of ionic conductance can change the dynamical states of the cell model (Figure 4 in [10] ). Doiron et al. have also suggested that the appropriate setting of the time constant value in dendritic potassium current inactivation is important for bursting dynamics (see the last paragraph of Section 3.3 in [8] ). However, how variations in the time constant values affect the ![]() -parameter space was not revealed in their study. Therefore, to contribute to an in-depth understanding of the kinetic properties of dendritic potassium current inactivation, in the present study, we performed numerical analysis and clarified the influence of time constant variations on the
-parameter space was not revealed in their study. Therefore, to contribute to an in-depth understanding of the kinetic properties of dendritic potassium current inactivation, in the present study, we performed numerical analysis and clarified the influence of time constant variations on the ![]() -parameter space.
-parameter space.
2. Materials and Methods
The ghostbursting model [Equations (1)-(6)] contains the following six state variables: the somatic membrane potential![]() , activating variable of the somatic delayed-rectifying potassium current
, activating variable of the somatic delayed-rectifying potassium current![]() , dendritic membrane potential
, dendritic membrane potential![]() , inactivating variable of the dendritic sodium current
, inactivating variable of the dendritic sodium current![]() , activating variable of the dendritic delayed-rectifying potassium current
, activating variable of the dendritic delayed-rectifying potassium current![]() , and inactivating variable of the dendritic delayed- rectifying potassium current
, and inactivating variable of the dendritic delayed- rectifying potassium current![]() . The time evolution of these variables is described with the following equations:
. The time evolution of these variables is described with the following equations:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where the definitions and values of the above-mentioned parameters are listed in Table 1. Equation (1) indicates that the time evolution of the somatic membrane potential ![]() is regulated by the fast inward sodium current
is regulated by the fast inward sodium current
![]()
Table 1. Values of the parameters in Equations (1)-(6) from [8] .
(the 2nd term), outward delayed-rectifying potassium current (the 3rd term), leak current (the 4th term), and electrotonic diffusive current between the somatic and dendritic compartments (the 5th term). Similarly, Equation (3) indicates that the time evolution of the dendritic membrane potential ![]() is regulated by the fast inward sodium current (the 1st term), outward delayed-rectifying potassium current (the 2nd term), leak current (the 3rd term), and electrotonic diffusive current between the somatic and dendritic compartments (the 4th term). Equations (2), (4), (5), and (6) indicate that the activating or inactivating variables approach the steady-state function
is regulated by the fast inward sodium current (the 1st term), outward delayed-rectifying potassium current (the 2nd term), leak current (the 3rd term), and electrotonic diffusive current between the somatic and dendritic compartments (the 4th term). Equations (2), (4), (5), and (6) indicate that the activating or inactivating variables approach the steady-state function
![]()
![]() at a rate that depends on the time constant
at a rate that depends on the time constant ![]()
![]() .
.
For detailed explanations of the model, see [8] .
The free and open source software Scilab (http://www.scilab.org/) was used to numerically solve equations (1)-(6) under the following initial conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . The response of the model to various
. The response of the model to various ![]() values was investigated under different values of
values was investigated under different values of![]() . The total simulation time was 1.2 s, and the constant depolarizing current pulse
. The total simulation time was 1.2 s, and the constant depolarizing current pulse ![]() was injected between 0.1 s and 1.1 s. Otherwise, the injected current was zero.
was injected between 0.1 s and 1.1 s. Otherwise, the injected current was zero.
3. Results
3.1. Reproduction of Previous Results
The ghostbursting model can show the three dynamical states: quiescence (Figure 1(a)), periodic tonic spiking (Figure 1(b)), and bursting (Figure 1(c)). The present study shows that the regions of these dynamical states in the ![]() -parameter space change in response to
-parameter space change in response to ![]() variations (Figure 2). The results at low
variations (Figure 2). The results at low ![]() are shown in Figure 2(a), those at intermediate
are shown in Figure 2(a), those at intermediate ![]() are shown in Figure 2(b), and those at high
are shown in Figure 2(b), and those at high ![]() are shown in Figure 2(c). First, in the present study, we performed a simulation of the model with
are shown in Figure 2(c). First, in the present study, we performed a simulation of the model with ![]() variable values set at
variable values set at ![]() (Figure 2(b)), which was the same condition as that used in Figure 6 in [8] . At a low
(Figure 2(b)), which was the same condition as that used in Figure 6 in [8] . At a low ![]() value (5.6 μA/cm2), the dynamical state of the model was that of quiescence, irrespective of the
value (5.6 μA/cm2), the dynamical state of the model was that of quiescence, irrespective of the ![]() value (× in Figure 2(b)). An example of the time course of the somatic membrane potential during the quiescent state is shown in Figure 1(a). At high
value (× in Figure 2(b)). An example of the time course of the somatic membrane potential during the quiescent state is shown in Figure 1(a). At high ![]() values (≥5.8 μA/cm2), the dynamical state was that of periodic tonic spiking (○ in Figure 2(b)) or bursting (● in Figure 2(b)). In other words, when the
values (≥5.8 μA/cm2), the dynamical state was that of periodic tonic spiking (○ in Figure 2(b)) or bursting (● in Figure 2(b)). In other words, when the ![]() value was small (≤12.0 mS/cm2), the dynamical state was that of bursting. In contrast, when the
value was small (≤12.0 mS/cm2), the dynamical state was that of bursting. In contrast, when the ![]() value was large (≥12.2 mS/cm2), the dynamical state was that of periodic tonic spiking at smaller
value was large (≥12.2 mS/cm2), the dynamical state was that of periodic tonic spiking at smaller ![]() values and that of bursting at larger
values and that of bursting at larger ![]() values, and the
values, and the ![]() threshold between periodic tonic spiking and bursting increased as the
threshold between periodic tonic spiking and bursting increased as the ![]() value was increased. Examples of the time courses of the somatic membrane potential during periodic tonic spiking and bursting are shown in Figure 1(b) and Figure 1(c), respectively. When the above-mentioned results were compared with previous findings (Figure 6 in [8] ), the present numerical analysis could reproduce the previous results.
value was increased. Examples of the time courses of the somatic membrane potential during periodic tonic spiking and bursting are shown in Figure 1(b) and Figure 1(c), respectively. When the above-mentioned results were compared with previous findings (Figure 6 in [8] ), the present numerical analysis could reproduce the previous results.
Based on the previous results (Figure 6 in [8] ), SNFP was thought to occur at certain ![]() values between × and ● in Figure 2(b). In addition, SNFP was thought to occur at certain
values between × and ● in Figure 2(b). In addition, SNFP was thought to occur at certain ![]() values between × and ○ in Figure 2(b). SNLC was thought to occur at certain
values between × and ○ in Figure 2(b). SNLC was thought to occur at certain ![]() values between ○ and ● in Figure 2(b). Codimension-two bifurcation was thought to occur at a certain
values between ○ and ● in Figure 2(b). Codimension-two bifurcation was thought to occur at a certain ![]() value that is surrounded by ×, ○, and ● in Figure 2(b).
value that is surrounded by ×, ○, and ● in Figure 2(b).
3.2. Effects of Changes in ![]() on the
on the ![]() -Parameter Space
-Parameter Space
The simulation results under conditions in which the ![]() value was decreased and increased are shown in Figure 2(a) and Figure 2(c), respectively. At a low Is value (5.6 μA/cm2), the dynamical state was that of quiescence, irrespective of the
value was decreased and increased are shown in Figure 2(a) and Figure 2(c), respectively. At a low Is value (5.6 μA/cm2), the dynamical state was that of quiescence, irrespective of the ![]() value (× in Figure 2(a) or Figure 2(c)), which is the same as that shown in Figure 2(b). The
value (× in Figure 2(a) or Figure 2(c)), which is the same as that shown in Figure 2(b). The ![]() threshold between quiescence and bursting, which is the boundary between × and ● in Figure 2(a) and Figure 2(c), is the same as that shown in Figure 2(b). The
threshold between quiescence and bursting, which is the boundary between × and ● in Figure 2(a) and Figure 2(c), is the same as that shown in Figure 2(b). The ![]() threshold between quiescence and periodic tonic spiking, which is the boundary between × and ○ in Figure 2(a) and Figure 2(c), is also the same as that shown in Figure 2(b). These results suggested that changes in the
threshold between quiescence and periodic tonic spiking, which is the boundary between × and ○ in Figure 2(a) and Figure 2(c), is also the same as that shown in Figure 2(b). These results suggested that changes in the ![]() values did not affect SNFP.
values did not affect SNFP.
At high ![]() values (≥5.8 μA/cm2), patterns similar to Figure 2(b) were observed. In other words, when the
values (≥5.8 μA/cm2), patterns similar to Figure 2(b) were observed. In other words, when the ![]() value was small (≤12.8 mS/cm2 in Figure 2(a) and ≤11.6 mS/cm2 in Figure 2(c)), the dynamical state was that of bursting only (● in Figure 2(a) and Figure 2(c)). In contrast, when the
value was small (≤12.8 mS/cm2 in Figure 2(a) and ≤11.6 mS/cm2 in Figure 2(c)), the dynamical state was that of bursting only (● in Figure 2(a) and Figure 2(c)). In contrast, when the ![]() value was large (≥13.0 mS/cm2 in Figure 2(a) and ≥11.8 mS/cm2 in Figure 2(c)), the dynamical state was that of periodic tonic
value was large (≥13.0 mS/cm2 in Figure 2(a) and ≥11.8 mS/cm2 in Figure 2(c)), the dynamical state was that of periodic tonic
spiking (○ in Figure 2(a) and Figure 2(c)) at smaller ![]() values and that of bursting at larger
values and that of bursting at larger ![]() values. The
values. The ![]() threshold between periodic tonic spiking and bursting increased as the
threshold between periodic tonic spiking and bursting increased as the ![]() value increased, as illustrated in Figure 2(a) and Figure 2(c). However, the
value increased, as illustrated in Figure 2(a) and Figure 2(c). However, the ![]() threshold between periodic tonic spiking and bursting differed among Figure 2(a), Figure 2(b), and Figure 2(c). In other words, an increase in the
threshold between periodic tonic spiking and bursting differed among Figure 2(a), Figure 2(b), and Figure 2(c). In other words, an increase in the ![]() value with fixed
value with fixed ![]() values increased the
values increased the ![]() threshold between periodic tonic spiking and bursting. These results suggested that changes in the
threshold between periodic tonic spiking and bursting. These results suggested that changes in the ![]() values had a great impact on SNLC and changes in the
values had a great impact on SNLC and changes in the ![]() values had no influence on the
values had no influence on the ![]() value of the codimension-two bifurcation point but had a great impact on the
value of the codimension-two bifurcation point but had a great impact on the ![]() value of the codimension-two bifurcation point.
value of the codimension-two bifurcation point.
4. Discussion
In the field of dynamical systems, it is important to investigate the dependence of the solutions of ordinary differential equations on system parameters. The present study illustrates the dependence of the qualitative nature of the solutions of ordinary differential equations on the following system parameters:![]() ,
, ![]() , and
, and![]() . In the ghost bursting model, there were three qualitatively different dynamical states: quiescence, spiking, and bursting. In particular, the present results revealed how the dynamical states of the two-dimensional
. In the ghost bursting model, there were three qualitatively different dynamical states: quiescence, spiking, and bursting. In particular, the present results revealed how the dynamical states of the two-dimensional ![]() - parameter space changed in response to variations in the third parameter
- parameter space changed in response to variations in the third parameter![]() . These results are important in that they imply a relationship between
. These results are important in that they imply a relationship between ![]() and bifurcation manifolds in the
and bifurcation manifolds in the ![]() -parameter space. In other words, these findings suggested that an increase in the
-parameter space. In other words, these findings suggested that an increase in the ![]() value did not shift the SNFP curve in the
value did not shift the SNFP curve in the ![]() -parameter space but rather shifted the SNLC curve upward. A very interesting finding in the present
-parameter space but rather shifted the SNLC curve upward. A very interesting finding in the present
study, which was not reported in the previous study [8] , is that there was a nonlinear relationship between ![]() and the area of the bursting state. In other words, although the amount of
and the area of the bursting state. In other words, although the amount of ![]() decrease was the same (−0.8 ms) between the changes from Figure 2(c) to Figure 2(b) and the changes from Figure 2(b) to Figure 2(a), the amount of increase in the area of the bursting state in the latter case was much larger than that in the former case.
decrease was the same (−0.8 ms) between the changes from Figure 2(c) to Figure 2(b) and the changes from Figure 2(b) to Figure 2(a), the amount of increase in the area of the bursting state in the latter case was much larger than that in the former case.
Other examples that illustrate how the dynamical states of two-dimensional parameter space change in response to variations in the third parameter are (1) a model of CA1 pyramidal neuron spiking dynamics (Figure 12 in [11] ) and (2) a compartmental model of Cheyne-Stokes respiration (Figure 5 in [12] ). In analysis of the CA1 model, Bianchi et al. have focused on the following three parameters: the injected current![]() , half-ac- tivation voltage of the transient sodium current
, half-ac- tivation voltage of the transient sodium current![]() , and half-activation voltage of the delay-rectifier potassium current
, and half-activation voltage of the delay-rectifier potassium current![]() . Their findings revealed that the dynamical states of the two-dimensional
. Their findings revealed that the dynamical states of the two-dimensional ![]() -parameter space hardly changed in response to variations in
-parameter space hardly changed in response to variations in![]() , while the dynamical states of the two-dimensional
, while the dynamical states of the two-dimensional ![]() -parameter space drastically changed in response to variations in
-parameter space drastically changed in response to variations in![]() . In analysis of the Cheyne-Stokes respiration model, Atamanyk and Langford focused on the following three parameters: the partial pressure of CO2 in the inspired air
. In analysis of the Cheyne-Stokes respiration model, Atamanyk and Langford focused on the following three parameters: the partial pressure of CO2 in the inspired air![]() , ventilation-perfusion ratio
, ventilation-perfusion ratio![]() , and slope of the Hill function
, and slope of the Hill function![]() . Their findings revealed that the two-dimensional
. Their findings revealed that the two-dimensional ![]() -parameter space was divided into stable equilibria and unstable equilibria regions by a Hopf bifurcation curve and that an increase in
-parameter space was divided into stable equilibria and unstable equilibria regions by a Hopf bifurcation curve and that an increase in ![]() shifted the Hopf bifurcation curve upward, resulting in an expansion of the stable equilibria region.
shifted the Hopf bifurcation curve upward, resulting in an expansion of the stable equilibria region.
Study [13] proposed an algorithm for the visualization of the bifurcation manifolds in the three-dimensional parameter space. In the three-dimensional parameter space, the parameter sets at which codimension one-bifur- cation occurs are visualized as bifurcation surfaces. Higher codimension bifurcations are located at intersections of the bifurcation surfaces. For example, analyses of a socioeconomic model have revealed codimension-one bifurcation surfaces: a Hopf bifurcation surface and a saddle-node bifurcation surface (Figure 5 in [13] ). In addition, the following codimension-two bifurcation curves were visualized: a Gavrilov-Guckenheimer bifurcation curve and a Takens-Bogdanov bifurcation curve. In contrast to the findings of the previous study [13] , in the present study, we did not visualize bifurcation manifolds in the three-dimensional ![]() -parameter space. However, when considering the changes in the dynamical states of the two-dimensional
-parameter space. However, when considering the changes in the dynamical states of the two-dimensional ![]() -para- meter space in response to variations in
-para- meter space in response to variations in ![]() (Figure 2), one can roughly imagine the bifurcation manifold in the three-dimensional
(Figure 2), one can roughly imagine the bifurcation manifold in the three-dimensional ![]() -parameter space. In other words, in the three-dimensional parameter space that is defined as a three-dimensional orthogonal coordinate system with axis lines
-parameter space. In other words, in the three-dimensional parameter space that is defined as a three-dimensional orthogonal coordinate system with axis lines![]() ,
, ![]() and
and![]() , the parameter sets at which SNFP occurs are thought to form the surface of SNFP that is orthogonal to the
, the parameter sets at which SNFP occurs are thought to form the surface of SNFP that is orthogonal to the ![]() plane, while the parameter sets at which SNLC occurs are thought to form the surface of SNLC that is not orthogonal to the
plane, while the parameter sets at which SNLC occurs are thought to form the surface of SNLC that is not orthogonal to the ![]() plane. The parameter sets at which codimension-two bifurcation occurs are thought to form a bifurcation curve at the intersection of the surfaces of SNFP and SNLC.
plane. The parameter sets at which codimension-two bifurcation occurs are thought to form a bifurcation curve at the intersection of the surfaces of SNFP and SNLC.
5. Conclusion
In conclusion, the novelty of this paper is that it reveals in detail the influence of ![]() variations on the dynamical states in the
variations on the dynamical states in the ![]() -parameter space of the ghostbursting model.
-parameter space of the ghostbursting model.
Acknowledgements
The author would like to thank Enago (www.enago.jp) for the English language review.