1. Introduction
Earthquakes occur around the world frequently. The most are so small that they cannot be susceptible, and only a few are large enough to cause a noticeable damage of building. When a structure is subjected to an earthquake motion, its base foundation tends to move with the ground.
One of the most important applications of structural dynamics is by analyzing the response of structures to ground shaking caused by an earthquake, whose data are useful for establishing the structural response spectra. The identification and evaluation of ground motion parameters require access to the measurements of strong ground motions in an actual earthquake [1] -[3] .
The basic element of an accelerograph is a transducer element as described in [4] [5] , which in its simplest form is a single-degree-of-freedom mass-damper-spring system. Typically, the transducer has natural frequency fn = 25 Hz and damping ratio ζ = 60% for modern analog accelerographs, and fn = 50 Hz and ζ = 70% for modern digit accelerographs [4] .
A simple stationary representation of earthquake-induced ground acceleration was proposed by Kanai [6] and Tajimi [7] , based on the study of frequency content of a number of strong ground motion records. They suggested that the ground acceleration of the earth surface layer could be approximated by the absolute acceleration of a simple oscillator with a concentrated mass supported by a linear spring and a dashpot. The spectrum property of an earthquake is reflected in its interaction with the structures which have different damping ratios and natural periods. In general, one can use the response spectrum, power spectrum or the Fourier spectrum to characterize the spectrum property of an earthquake. In this paper we propose a novel method to characterize the earthquake property when it is exerted on a simple one-degree-of-freedom system:
 (1)
(1)
where 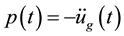 is the ground acceleration due to an earthquake; ζ is the damping ratio; and ωn is the natural frequency.
is the ground acceleration due to an earthquake; ζ is the damping ratio; and ωn is the natural frequency.
The ground motion produced by earthquake can be very complicated. The exact form of earthquakes is subjected to a high degree of uncertainty and complexity. There are several ways to estimate the ground motion parameters, which are essential for describing the important characteristics of strong ground motion in a compact quantitative form. Because of the complexity of the earthquake ground motion, the identification of a single parameter that can accurately describe all important ground motion characteristics is impossible. In this paper we try to use the barcode and the percentage of the first set of dis-connectivity in the barcode to reflect the characteristic property of an earthquake ground motion. It is known that a barcode is an optical machine-readable representation of data relating to the object to which it is attached. A main feature of the barcode is the intervened black lines and white lines with varying spacings and widths. Barcode is ubiquitously used in the identification and classification of human made products. Here we will use the barcode to identify the property of earthquake with the input  in Equation (1).
in Equation (1).
2. A System Formulation
To facilitate the formulation we write a system of first-order ordinary differential equations (ODEs):
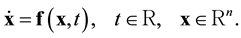 (2)
(2)
Here n = 2, 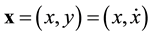 , and two components of f are
, and two components of f are 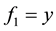 and
and 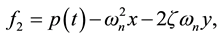 respectively.
respectively.
As that done by Liu [8] , for Equation (2) we can define a unit orientation vector:
 (3)
(3)
where 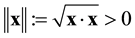 is the Euclidean norm of x, and the dot between two vectors, say
is the Euclidean norm of x, and the dot between two vectors, say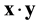 , denotes the inner product of x and y. Then we can derive [9] - [11]
, denotes the inner product of x and y. Then we can derive [9] - [11]
![]() (4)
(4)
![]() (5)
(5)
Equations (4) and (5) can be put together as
![]() (6)
(6)
which is a Lie-type system endowing with the Lie-group symmetry SOo(n, 1) in the Minkowski space.
3. Two Branches Solutions
In order to develop a numerical scheme from Equation (6), we suppose that the coefficient matrix is constant with the pair
![]() (7)
(7)
being constant in a small time stepsize.
From Equations (6) and (7) we thus need to solve a constant linear system:
![]() (8)
(8)
Let
![]() (9)
(9)
![]() (10)
(10)
and Equation (8) becomes
![]() (11)
(11)
![]() (12)
(12)
At the same time, from the above equations we can derive the following ODEs for z, w and y:
![]() (13)
(13)
where ![]() Fortunately, the original
Fortunately, the original ![]() -dimensional problem in Equation (8) can be reduced to a three- dimensional problem in Equation (13). Depending on the signum function of
-dimensional problem in Equation (8) can be reduced to a three- dimensional problem in Equation (13). Depending on the signum function of
![]() (14)
(14)
there exist two different types solutions of (z, w, y). Here, we do not give a detailed derivation of the solutions for (z, w, y) and the corresponding second generation group preserving scheme (GPS2), but the reader can refer [9] - [11] .
4. The Demonstration of Barcodes
It is significant that in Equation (14) we have derived a signum function to demand the algorithm into two branches. Without having the factor 2 before ![]() in Equation (14) one has
in Equation (14) one has
![]()
where θ is the intersection angle between x and f; hence, it makes no sense to define its signum function. On the contrast, by Equation (14) we have
![]() (15)
(15)
which may be +1 or −1, depending on x and f by their intersection angle θ. When θ is in the range of ![]() or
or![]() , the value of Sign is Sign = −1; otherwise, Sign = +1. Thus we can observe the time-varying values of Sign and plot them as a barcode. In order to demonstrate the use of barcode, let us investigate the following examples. In all computations given below the initial conditions are set to be
, the value of Sign is Sign = −1; otherwise, Sign = +1. Thus we can observe the time-varying values of Sign and plot them as a barcode. In order to demonstrate the use of barcode, let us investigate the following examples. In all computations given below the initial conditions are set to be![]() , unless specifying otherwise.
, unless specifying otherwise.
4.1. Example 1
First we test an example with ![]() and
and![]() , and a harmonic force p(t) = cost is applied to Equa-
, and a harmonic force p(t) = cost is applied to Equa-
tion (1) in a time interval of![]() . The input, the following signum function:
. The input, the following signum function:
![]() (16)
(16)
where ![]() and
and ![]() and the responses of x(t) and y(t) are plotted in Figure 1. It is interesting that after 0.78 sec, Sign = +1 for the harmonic input. As compared with the closed- form solution, in Figure 1(d) we plot the numerical error, which is quite accurate, and is smaller than the time stepsize h = 0.001 used in this computation.
and the responses of x(t) and y(t) are plotted in Figure 1. It is interesting that after 0.78 sec, Sign = +1 for the harmonic input. As compared with the closed- form solution, in Figure 1(d) we plot the numerical error, which is quite accurate, and is smaller than the time stepsize h = 0.001 used in this computation.
![]()
Figure 1. Under (a) a harmonic force, showing (b) the signum function, (c) the responses, and (d) numerical error of displacement.
4.2. Example 2
Then with ![]() and
and![]() , and under a random force
, and under a random force
![]() (17)
(17)
where Ri are random numbers between [−1, 1], the input, the Sign and the responses are plotted in Figure 2. It is interesting that the values of Sign are randomly jumping between +1 and −1 in some intervals of time.
4.3. Analyzing the Barcode under Earthquakes
With ![]() and
and![]() , and under the El Centro earthquake
, and under the El Centro earthquake![]() , which is adjusted to
, which is adjusted to ![]() as the input to Equation (1), the barcode and the responses are plotted in Figure 3. As shown in Figure 3(b), the time history of Sign looks like a barcode, which is interesting that the values of Sign are frequently jumping between +1 and −1 with a certain structure.
as the input to Equation (1), the barcode and the responses are plotted in Figure 3. As shown in Figure 3(b), the time history of Sign looks like a barcode, which is interesting that the values of Sign are frequently jumping between +1 and −1 with a certain structure.
Now we analyze the Sign and the length as shown in Figure 4 within a short time interval of![]() , which is starting from the initial conditions
, which is starting from the initial conditions![]() , where we take
, where we take ![]() and
and ![]() and
and ![]() being the input. First we note that the length as governed by Equation (5) has the following property:
being the input. First we note that the length as governed by Equation (5) has the following property:
![]()
Figure 2. Under (a) a random force, showing (b) the signum function, and (c) the responses.
![]()
Figure 3. Under (a) the El Centro earthquake, showing (b) the barcode, and (c) the responses.
![]() (18)
(18)
where![]() . Then, as a schematic plot shown in Figure 5, there are two dis-connected sets of
. Then, as a schematic plot shown in Figure 5, there are two dis-connected sets of ![]() in the hyper-plane (x, f):
in the hyper-plane (x, f):
![]() (19)
(19)
![]() (20)
(20)
We may call them the first set of dis-connectivity and the second set of dis-connectivity, respectively. Clearly, the first set of dis-connectivity is a subset of sign(c0) = +1, and the second set of dis-connectivity is a subset of sign(c0) = −1.
If Equation (2) satisfies
![]()
Figure 4. Under the El Centro earthquake, (a) showing two signum functions, and (b) the length with a small time interval.
![]()
Figure 5. A schematic plot of the area of Sign = +1, Sign = −1, sign(c0) = +1, and sign(c0) = −1 in the plane.
![]() (21)
(21)
Under the first assumption the case in Equation (20) is impossible because it contradicts to
![]() . Then under the condition of
. Then under the condition of![]() , it is always
, it is always
![]() (22)
(22)
because the two sets of dis-connectivity are dis-connected, and from the first set to the second set it must go to
![]() in some time interval. Then using Equations (5) and (22) we have
in some time interval. Then using Equations (5) and (22) we have
![]() (23)
(23)
which means that the length grows with time. Thus, Equation (21) is proven.
For a system being excited by earthquake the value of Sign is not always +1 as that shown in Figure 1(b) for the harmonic input. As shown in Figure 3(b) the values of Sign are varying between −1 to +1 and +1 to −1 very fast, and then the Sign will return to +1 again as shown in Figure 4(a); otherwise, by Equation (21) the system will respond unstably and thus the displacement will tend to infinity. In order to compare the values of sign(c0) with the values of Sign we plot them in Figure 4(a) with solid line and dashed line, respectively, where we make a slight shift of the dashed line downward for clear. On the other hand, for a distinction the first set of dis-con- nectivity is filled by solid black points.
As shown in Figure 5, in the plane the areas of sign(c0) = +1 and sign(c0) = −1 are connected while that the sets of Sign = +1 and Sign = −1 are dis-connected as mentioned in the above. When sign(c0) changes from +1 to −1, for example from point f1 to point f2 in the figure, the Sign must jump from −1 to +1. This jumping behavior is termed a cross jumping. On the other hand, we also find the co-jumping behavior which is happened when both the Sign and sign(c0) are jumping from −1 to +1 simultaneously. The above two jumping behaviors are collected as a coupled-jumping, which renders a quite complex structure of the barcode as shown in Figure 3(b).
From Figure 4(a) we can observe the following interesting phenomena: 1) While the first set of dis-connec- tivity is a subset of sign(c0) = +1, the second set of dis-connectivity is a subset of sign(c0) = −1. 2) In a time interval of the state with Sign = −1, the state is either in the first set of dis-connectivity or in the second set of dis- connectivity. 3) From one first set of dis-connectivity to another first set of dis-connectivity there must accompany a jump from Sign = −1 to Sign = +1. This also holds for the second set of dis-connectivity. 4) From one first set of dis-connectivity to one second set of dis-connectivity, or vice-versa, there must accompany a jump from Sign = −1 to Sign = +1. For some cases this jumping only happens at one time point. 5) When sign(c0) jumps from +1 to −1 as remarked in Figure 4(a) by the symbols + and − (i.e., the length is decreased), and if the Sign is in the state of −1, then the Sign will jump from −1 to +1 as remarked in Figure 4(a) by the symbols − and +. Indeed in Figure 4(a) we can observe that there are four times to happen the cross jumping behavior in the interval of![]() . Besides the first one, the other three times are marked by the Arabic numbers 2, 3 and 4 in Figure 4(a). Besides, there is also a co-jumping as remarked in Figure 4(a). The proof of 5) is obvious by viewing Figure 5 that the first set of Sign = −1 cannot directly jump to the second set of Sign = −1. When f1 goes to f2, the Sign changes from −1 to +1.
. Besides the first one, the other three times are marked by the Arabic numbers 2, 3 and 4 in Figure 4(a). Besides, there is also a co-jumping as remarked in Figure 4(a). The proof of 5) is obvious by viewing Figure 5 that the first set of Sign = −1 cannot directly jump to the second set of Sign = −1. When f1 goes to f2, the Sign changes from −1 to +1.
In Figure 6 we compare the barcodes with 1)![]() ,
, ![]() and
and![]() , 2)
, 2)![]() ,
, ![]() and
and![]() , 3)
, 3)![]() ,
, ![]() and
and![]() , and 4)
, and 4)![]() ,
, ![]() and
and![]() .
.
4.4. The First Set of Dis-Connectivity under Earthquakes
In this example we let the Chi-Chi earthquake be the input to Equation (1). With ![]() and
and![]() , and under the Chi-Chi earthquake
, and under the Chi-Chi earthquake ![]() recorded at the station of CHY028, we adjust it to be
recorded at the station of CHY028, we adjust it to be ![]() as shown in Figure 7(a). The barcode and the responses are plotted in Figure 7(b) and Figure 7(c).
as shown in Figure 7(a). The barcode and the responses are plotted in Figure 7(b) and Figure 7(c).
In Figure 8 we compare the barcodes with 1)![]() ,
, ![]() and
and![]() , 2)
, 2)![]() ,
, ![]() and
and![]() , 3)
, 3)![]() ,
, ![]() and
and![]() , and 4)
, and 4)![]() ,
, ![]() and
and![]() .
.
In Figure 9(a) for the Chi-Chi earthquake with different scaling factor fr in ![]() as being the input to Equation (1), and with
as being the input to Equation (1), and with ![]() and
and![]() , we plot the percentage in the first set of dis-connec- tivity in Figure 9(b), which is near to forty eight percentage, and at the same time we also display the numbers
, we plot the percentage in the first set of dis-connec- tivity in Figure 9(b), which is near to forty eight percentage, and at the same time we also display the numbers
![]()
Figure 6. Under the El Centro earthquake, comparing the barcodes under different scaling factor, damping ratio and natural period.
of coupled-jumping as discussed above with respect to the scaling factor fr in Figure 9(c). It can be seen that the number is either 24 or 25. In the plane as shown in Figure 5, the first set of dis-connectivity with Sign = −1 is only in one quarter. But under a strong earthquake, the high occupation of the first set of dis-connectivity is near to fifty percentage as shown in Figure 9(b).
In Figure 10, under the Chi-Chi earthquake (CHY080) as shown in (a), we plot the first set of dis-connectiv- ity which is near to forty nine percentage as shown in Figure 10(b), and the number of coupled-jumping is plotted in Figure 10(c), which is either 6 or 7.
In Figure 11(a) for the El Centro earthquake (ELC180) with different scaling factor fr in![]() , and with
, and with ![]() and
and![]() , we plot the first set of dis-connectivity which is near to forty six percentage as shown in Figure 11(b), and the number of coupled-jumping is plotted in Figure 11(c), which is 0 or 1 for most scaling factors. In Figure 12(a) for the Loma Prieta earthquake (47379 Gilroy Array # 1) with different scaling factor fr in
, we plot the first set of dis-connectivity which is near to forty six percentage as shown in Figure 11(b), and the number of coupled-jumping is plotted in Figure 11(c), which is 0 or 1 for most scaling factors. In Figure 12(a) for the Loma Prieta earthquake (47379 Gilroy Array # 1) with different scaling factor fr in![]() , and with
, and with ![]() and
and![]() , we plot the first set of dis-connectivity which is near to forty six percentage as shown in Figure 12(b), and the number of coupled-jumping is plotted in Fig- ure 12(c), which is between 1 to 7.
, we plot the first set of dis-connectivity which is near to forty six percentage as shown in Figure 12(b), and the number of coupled-jumping is plotted in Fig- ure 12(c), which is between 1 to 7.
It is surprising that the percentage of the first set of disconnectivity and the number of coupled-jumping are almost constant for each earthquake, which seems to be scale-invariant. In the plane as shown in Figure 5, the
![]()
![]()
![]()
Figure 7. Under the Chi-Chi earthquake (CHY028) in (a), (b) showing the barcode, and (c) the responses.
first set of dis-connectivity with Sign = −1 is only in one quarter. But under strong earthquakes, the high occupation of the first set of dis-connectivity is near to fifty percentage. The high percentage of occupation demonstrates the importance of the first set of dis-connectivity in the strong earthquake motion. As comparing the above four earthquakes we can also observe that stronger earthquake leads to larger percentage of the first set of dis-connectivity. Finally, under the same scaling factor fr = 0.5 in ![]() and the same
and the same ![]() and
and![]() , in Figure 13 we compare the relative percentages of first set of dis-connectivity for the El Centro earthquake (ELC180), the Loma Prieta earthquake (47379 Gilroy Array #1), and two records (CHY028, CHY080) of Chi-Chi earthquake. The relative percentage is a time history of the time-duration of the first set of dis-connectivity, whose time is dividing by the total time of earthquake. This figure reflects that the Chi-Chi earthquake has larger values than that of the El Centro and the Loma Prieta earthquakes, and CHY080 is larger than CHY028. This can also be explained by calculating the power of earthquake with the
, in Figure 13 we compare the relative percentages of first set of dis-connectivity for the El Centro earthquake (ELC180), the Loma Prieta earthquake (47379 Gilroy Array #1), and two records (CHY028, CHY080) of Chi-Chi earthquake. The relative percentage is a time history of the time-duration of the first set of dis-connectivity, whose time is dividing by the total time of earthquake. This figure reflects that the Chi-Chi earthquake has larger values than that of the El Centro and the Loma Prieta earthquakes, and CHY080 is larger than CHY028. This can also be explained by calculating the power of earthquake with the ![]() -norm of earth- quake, of which the power value of CHY080 is 0.7765, of CHY028 is 0.6193 and of the El Centro earthquake is 0.3444. The Loma Prieta earthquake (47379 Gilroy Array #1) leads to a close curve with that produced by the El Centro earthquake, whose power is 0.33.
-norm of earth- quake, of which the power value of CHY080 is 0.7765, of CHY028 is 0.6193 and of the El Centro earthquake is 0.3444. The Loma Prieta earthquake (47379 Gilroy Array #1) leads to a close curve with that produced by the El Centro earthquake, whose power is 0.33.
5. Conclusions
For a single-degree-of-freedom system subjected to an earthquake excitation, we have investigated the response
![]()
Figure 8. Under the Chi-Chi earthquake (CHY028), comparing the barcodes under different scaling factor, damping ratio and natural period.
behavior from a newly developed theory about the dynamical system of ![]() by viewing the signum function of
by viewing the signum function of ![]() The main idea in this paper is that the earthquake will make the function f highly complex in time, even the linear system is simple in x. Under this situation, we expect that the signum function being a time varying function will disclose the complexity of earthquake, such that we can study its structure. The barcode was formed by plotting the signum function Sign with respect to the time history of an earthquake. We have analyzed the jumping behavior from two famous earthquake inputs of 1940 El Centro earthquake and 1999 Chi-Chi earthquake. Several barcodes were used to reveal a quite complex structure of earthquake, and we have demonstrated the importance of the first set of dis-connectivity, whose high percentage occupation is very interesting when one considers the linear system under a strong earthquake. Through the comparisons of four earthquake inputs, we have observed that stronger earthquake leads to larger percentage of the first set of dis-connectivity. The coupled-jumping behavior may happen due to the random property of
The main idea in this paper is that the earthquake will make the function f highly complex in time, even the linear system is simple in x. Under this situation, we expect that the signum function being a time varying function will disclose the complexity of earthquake, such that we can study its structure. The barcode was formed by plotting the signum function Sign with respect to the time history of an earthquake. We have analyzed the jumping behavior from two famous earthquake inputs of 1940 El Centro earthquake and 1999 Chi-Chi earthquake. Several barcodes were used to reveal a quite complex structure of earthquake, and we have demonstrated the importance of the first set of dis-connectivity, whose high percentage occupation is very interesting when one considers the linear system under a strong earthquake. Through the comparisons of four earthquake inputs, we have observed that stronger earthquake leads to larger percentage of the first set of dis-connectivity. The coupled-jumping behavior may happen due to the random property of
![]()
Figure 9. Under (a) the Chi-Chi earthquake (CHY028) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
![]()
Figure 10. Under (a) the Chi-Chi earthquake (CHY080) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
![]()
Figure 11. Under (a) the El Centro earthquake (ELC180) with different scaling factor, showing (b) the percentage in the first set of dis-connec- tivity, and (c) the number of coupled-jumping.
![]()
Figure 12. Under (a) the 1989 Loma Prieta earthquake (47379 Gilroy Array #1) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
![]()
Figure 13. Comparing the relative percentages of first set of dis-con- nectivity for the El Centro earthquake (ELC180), two records (CHY028, CHY080) of Chi-Chi earthquake, and the Loma Prieta earthquake (47379 Gilroy Array #1).
earthquakes, and its number seems scale-independence. This is just an initial study by correlating the percentage of the first set of dis-connectivity to the earthquake, and there are still many works to study the barcode and the use of it to forecast the intensity of earthquake before the rapid coming of main shock impulse. In the future, we will analyze the signal of barcode for many earthquake records, and thus we can correlate the intensity and frequency content of an earthquake to the first set of dis-connectivity.