Symmetry Analysis for MHD Viscous Flow and Heat Transfer over a Stretching Sheet ()
1. Introduction
The boundary layer flow and heat transfer of an incompressible viscous fluid over a stretching sheet appear in several manufacturing processes of industry such as the aerodynamic extrusion of plastic sheets, the extrusion of polymers, hot rolling, the cooling of metallic plates, glass-fiber production, etc., [1] .
Sakiadis [2] presented the pioneering work in this field. He investigated the flow induced by a semi-infinite horizontally moving wall in an ambient fluid.
Crane [3] studied the flow over a linearly stretching sheet in an ambient fluid and gave a similarity solution in closed analytical form for the steady two-dimensional problem. He presented a closed form exponential solution for the planar viscous flow of linear stretching case.
Gupta and Gupta [4] investigated the effect of mass transfer on the Crane flow. They analyzed the viscous flow and heat transfer by an isothermal stretching sheet with suction/injection.
Chiam [5] studied the boundary layer flow due to a plate stretching with a power-low velocity distribution in presence of a magnetic field. To yield similarity equations, a special form of the magnetic field is chosen. He presented linearized solutions for the case of large magnetic parameters and derived an expression for the skin friction coefficient using Crocco’s transformation and compared it numerically using Runge-Kutta shooting algorithm with Newton iteration.
Vajravelu [6] studied flow and heat transfer in a viscous fluid over a non-linear stretching sheet. In his study, the heat transfer is analyzed when the sheet is maintained at a constant temperature and the viscous dissipation is neglected. He used a fourth-order Runge-Kutta integration scheme to solve the resulting nonlinear differential equations.
Cortell [7] presented a numerical analysis for the flow and heat transfer in a viscous fluid over a nonlinear stretching sheet by employing a novel numerical procedure. In his work, he studied two cases for the nonlinear stretching sheet, with constant surface temperature and with prescribed surface temperature. The resulting nonlinear ordinary differential equations after converting the governing partial differential equations by a similarity transformation are solved using Runge-Kutta scheme.
Abbas and Hayat [8] studied the radiation effects on the magnetohydrodynamic (MHD) flow of an incompressible viscous fluid in a porous space. In their study, they extended the analysis of Cortell [7] by considering a MHD flow, analyzed the flow in a porous medium, included the radiation effects and provided analytic solution namely homotopy analysis method (HAM) instead of numerical technique applied in [7] . Hayat et al. [9] investigated the magnetohydrodynamic (MHD) boundary layer flow by employing the modified Adomian decomposition method and the Padé approximation and developed the series solution of the governing non-linear problem.
Ghotbi [10] considered the problem of the boundary layer flow of an incompressible viscous fluid over a non- linear stretching sheet. In order to obtain analytical solution of the governing nonlinear differential equations, HAM is applied.
Mehmood et al. [11] reported the corrections to HAM results presented in [10] . A comparison between their HAM solution and the exact solution obtained by Pavlov [12] was made and it was in a good agreement.
Javed et al. [13] investigated the boundary layer flow and heat transfer analysis of electrically conducting viscous fluid over a nonlinearly shrinking sheet. They used a similarity transformation to reduce the governing partial differential equations to a set of nonlinear ordinary differential equations. The resulting system of equations is then solved numerically using an implicit finite difference scheme known as Keller-box method.
Fathizadeh et al. [14] employed the modification of the homotopy perturbation method to solve the MHD boundary-layer equations. In their work, the viscous fluid is electrically conducting in the presence of a uniform applied magnetic field and the induced magnetic field is neglected for small magnetic Reynolds number. They obtained the similarity solutions of ordinary differential equation resulting from the momentum equation. Some numerical comparisons among the new modified homotopy perturbation method, the standard homotopy perturbation, the exact solution and the shooting method are obtained.
In this paper, we shall investigate the solution of the MHD boundary layer flow for an incompressible viscous fluid over a sheet stretching according to a power-law velocity. Lie-group theory is applied to the equations of motion for determining symmetry reductions of partial differential equations [15] - [30] . The resulting system of nonlinear differential equations is then solved numerically using shooting method coupled with Runge-Kutta scheme. Our results are compared with the work of [5] - [14] .
2. Mathematical Formulation of the Problem
We consider the MHD flow over a flat plate coinciding with the plane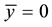 , of an incompressible viscous fluid with heat transfer. The wall is stretched horizontally by applying on both sides two equal and opposite forces along the
, of an incompressible viscous fluid with heat transfer. The wall is stretched horizontally by applying on both sides two equal and opposite forces along the 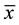 -axis to keep the origin fixed. The fluid is electrically conducting under the influence of an applied magnetic field
-axis to keep the origin fixed. The fluid is electrically conducting under the influence of an applied magnetic field 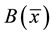 in the
in the  -direction normally to the stretching sheet, Figure 1.
-direction normally to the stretching sheet, Figure 1.
The induced magnetic field is neglected. Under these assumptions, the continuity, momentum and energy equations become
![]()
Figure 1. Physical model and coordinate system.
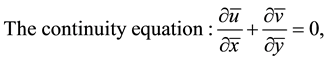 (2.1)
(2.1)
 (2.2)
(2.2)
 (2.3)
(2.3)
where  and
and , are the velocity components in the
, are the velocity components in the  and
and  directions, respectively,
directions, respectively,  is the kinematic viscosity,
is the kinematic viscosity, 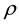 is the fluid density,
is the fluid density, 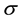 is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid,  is the specific heat of the fluid at constant pressure,
is the specific heat of the fluid at constant pressure, ![]() is the thermal conductivity of the fluid, and
is the thermal conductivity of the fluid, and ![]() is the temperature.
is the temperature.
The magnetic field is defined by
![]() , (2.4)
, (2.4)
where ![]() and
and ![]() are constants.
are constants.
The boundary conditions are
![]() (2.5)
(2.5)
where ![]() is a constant,
is a constant, ![]() is the uniform temperature of the stretching sheet and
is the uniform temperature of the stretching sheet and ![]() is the temperature at large distance from the wall, where
is the temperature at large distance from the wall, where![]() .
.
The variables in Equations (2.1)-(2.5) are dimensionless according to
![]() , (2.6)
, (2.6)
where ![]() is the characteristic velocity.
is the characteristic velocity.
Substitution from Equation (2.6) into Equations (2.1)-(2.3) gives
![]() (2.7)
(2.7)
![]() , (2.8)
, (2.8)
![]() , (2.9)
, (2.9)
where, ![]() is a constant,
is a constant, ![]() is the Prandtl number, and
is the Prandtl number, and ![]() is the dynamic viscosity. Without losing of generality, let,
is the dynamic viscosity. Without losing of generality, let,![]() .
.
The boundary conditions Equation (2.5) will be
![]() (2.10)
(2.10)
From the continuity Equation (2.7) there exist stream function ![]() such that,
such that,
![]() (2.11)
(2.11)
which satisfies Equation (2.7) identically.
Substituting from Equation (2.11) into Equations (2.8)-(2.9), yields
![]() , (2.12)
, (2.12)
![]() , (2.13)
, (2.13)
where subscripts denote partial derivatives.
The boundary conditions Equation (2.8) will be
![]() (2.14)
(2.14)
3. Solution of the Problem
Firstly, we derive the similarity solutions using Lie-group method under which Equations (2.12)-(2.13) and the boundary conditions Equation (2.14) are invariant, and then we use these symmetries to determine the similarity variables.
Consider the one-parameter ![]() Lie group of infinitesimal transformations in
Lie group of infinitesimal transformations in ![]() given by
given by
![]() (3.1)
(3.1)
where “![]() ” is the group parameter.
” is the group parameter.
A system of partial differential Equations (2.12)-(2.13) is said to admit a symmetry generated by the vector field
![]() , (3.2)
, (3.2)
if it is left invariant by the transformation![]() .
.
The solutions ![]() and
and![]() , are invariant under the symmetry Equation (3.2) if
, are invariant under the symmetry Equation (3.2) if
![]() , (3.3)
, (3.3)
and
![]() . (3.4)
. (3.4)
Assume,
![]() , (3.5)
, (3.5)
![]() . (3.6)
. (3.6)
A vector ![]() given by Equation (3.2), is said to be a Lie point symmetry vector field for Equations (2.12)- (2.13) if
given by Equation (3.2), is said to be a Lie point symmetry vector field for Equations (2.12)- (2.13) if
![]() (3.7)
(3.7)
where,
![]() (3.8)
(3.8)
is the third prolongation of![]() .
.
To calculate the prolongation of the given transformation, we need to differentiate Equation (3.1) with respect to each of the variables, ![]() and
and![]() . To do this, we introduce the following total derivatives
. To do this, we introduce the following total derivatives
![]() (3.9)
(3.9)
Equation (3.7) gives the following linear partial differential equation
![]() , (3.10)
, (3.10)
![]() (3.11)
(3.11)
The components![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() can be determined from the following expressions
can be determined from the following expressions
![]() (3.12)
(3.12)
where ![]() and
and ![]() are stand for
are stand for ![]() and
and![]() .
.
Invariance of the boundary conditions Equation (2.14i), yields
![]() . (3.13)
. (3.13)
Substitution from Equations (3.12)-(3.13) into Equation (3.11) will lead to a large expression, then, equating to zero the coefficients of![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , gives
, gives
![]() . (3.14)
. (3.14)
Substitution from Equation (3.14) into Equation (3.11) will remove many terms. Then, equating to zero the coefficients of ![]() and
and![]() , leads to the following system of determining equations:
, leads to the following system of determining equations:
![]() (3.15)
(3.15)
![]() . (3.16)
. (3.16)
Again, substitution from Equations (3.12)-(3.16) into Equation (3.10) will remove many terms. Then, equating to zero the coefficients of![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , gives
, gives
![]() , (3.17)
, (3.17)
and
![]() . (3.18)
. (3.18)
Solving the system of Equations (3.14)-(3.18) in view of the invariance of the boundary conditions Equation (2.14), yields
![]() (3.19)
(3.19)
The system of nonlinear Equations (2.12)-(2.13) has the three-parameter Lie group of point symmetries generated by
![]() (3.20)
(3.20)
The one-parameter group generated by ![]() consists of scaling, whereas
consists of scaling, whereas ![]() and
and ![]() consists of translation. The commutator table of the symmetries is given in Table 1, where the entry in the i-th row and j-th column is defined as
consists of translation. The commutator table of the symmetries is given in Table 1, where the entry in the i-th row and j-th column is defined as![]() .
.
The finite transformations corresponding to the symmetries![]() ,
, ![]() and
and ![]() are respectively
are respectively
![]() , (3.21)
, (3.21)
where![]() ,
, ![]() and
and ![]() are the group parameters.
are the group parameters.
We look for solutions that invariant under the linear combination of the operators given by Equation (3.20). By determine the one-dimensional optimal system of subalgebras of the given partial differential equation, all of these solutions can be obtained. Olver’s approach given in [17] starts out by computing the commutators of the
![]()
Table 1. Table of commutators of the basis operators.
symmetry Lie algebra Equation (3.20) and then obtaining the adjoint representations. The adjoint action on Lie algebras is defined by the adjoint operator given by
![]() , (3.22)
, (3.22)
where, ![]() is a small parameter.
is a small parameter.
In terms of Lie brackets using Campbell-Baker-Hausdorff theorem [31] , this operator can be rewritten as
![]() . (3.23)
. (3.23)
In our problem, ![]() is the Lie algebra associated with the symmetry group. The calculations of the adjoint action are summarized in Table 2.
is the Lie algebra associated with the symmetry group. The calculations of the adjoint action are summarized in Table 2.
To construct the one-dimensional optimal system of![]() , consider a general element of
, consider a general element of ![]() given by
given by
![]() , (3.24)
, (3.24)
for some constants![]() ,
, ![]() and
and![]() , and probe whether
, and probe whether ![]() can be transformed to a new element
can be transformed to a new element ![]() under the general adjoint action, where
under the general adjoint action, where ![]() takes a simpler form than
takes a simpler form than![]() , [32] .
, [32] .
Let,
![]() . (3.25)
. (3.25)
We make appropriate choice of ![]() such that the
such that the![]() ’s can be made 0 or 1. We end up with simpler forms of
’s can be made 0 or 1. We end up with simpler forms of ![]() that will constitute the one-dimensional optimal system.
that will constitute the one-dimensional optimal system.
By substitution ![]() in Equation (3.25) and dropping the primes, we get
in Equation (3.25) and dropping the primes, we get
![]() . (3.26)
. (3.26)
Now, Equation (3.26) prompts the consideration of the cases ![]() and
and![]() .
.
Case (1): ![]()
By choosing ![]() and scaling the resulting operator by
and scaling the resulting operator by![]() , Equation (3.26) will be
, Equation (3.26) will be
![]() . (3.27)
. (3.27)
We can further consider the subcases ![]() and
and![]() . Therefore, an optimal system of one-dimensional subalgebra for this case is given by
. Therefore, an optimal system of one-dimensional subalgebra for this case is given by![]() , where,
, where,![]() .
.
Case (2): ![]()
Using repeatedly the adjoint operation to simplify![]() , an optimal system of one-dimensional subalgebra for this case is given by
, an optimal system of one-dimensional subalgebra for this case is given by![]() , where,
, where,![]() .
.
In summary, the optimal system of one-dimensional subalgebras of the symmetry Lie algebra is
![]() . (3.28)
. (3.28)
Table 3 shows the solution of the invariant surface conditions associated with the optimal system.
(i) Solutions invariant under![]() :
:
The characteristic
![]()
Table 2. Table of adjoint representations.
![]()
Table 3. Solutions of the invariant surface conditions associated with the optimal system.
![]() , (3.29)
, (3.29)
has the components
![]() (3.30)
(3.30)
Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are
![]() (3.31)
(3.31)
where ![]() is the similarity variable.
is the similarity variable.
Substitution from Equation (3.31) into Equations (2.12)-(2.13), yields
![]() , (3.32)
, (3.32)
![]() , (3.33)
, (3.33)
where, ![]() and
and ![]() is the magnetic parameter, where
is the magnetic parameter, where ![]() is the Hartmann number.
is the Hartmann number.
The boundary conditions Equation (2.14) will be
![]() (3.34)
(3.34)
(ii) Solutions invariant under![]() :
:
The characteristic Equation (3.29) has the components
![]() (3.35)
(3.35)
Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are
![]() (3.36)
(3.36)
Practically, Equation (3.36) is a solution of Equations (2.12)-(2.13), even though it is not a particularly interesting one which contradicts the boundary conditions Equation (2.14). So, no solutions are invariant under the group generated by![]() .
.
(iii) Solutions invariant under![]() :
:
The characteristic Equation (3.29) has the components
![]() (3.37)
(3.37)
Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are
![]() (3.38)
(3.38)
where ![]() is the similarity variable, which gives the same solutions invariant under
is the similarity variable, which gives the same solutions invariant under![]() .
.
(iv) Solutions invariant under![]() :
:
The characteristic Equation (3.29) has the components
![]() (3.39)
(3.39)
Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are
![]() (3.40)
(3.40)
This contradicts the boundary conditions Equation (2.14). So, no solutions are invariant under the group generated by![]() .
.
4. Results and Discussion
The system of non-linear differential Equations (3.32)-(3.33) with the boundary conditions Equation (3.34) is solved numerically using the shooting method, coupled with Runge-Kutta scheme. From Equations (2.11) and (3.31), we get
![]() . (4.1)
. (4.1)
The effects of the parameter ![]() which is a function of the power-index
which is a function of the power-index![]() , the Hartmann number
, the Hartmann number![]() , and the Prandtl number
, and the Prandtl number ![]() on the horizontal and vertical velocities, and temperature profiles are illustrated in Figures 2-8. Moreover, the numerical values of the skin friction
on the horizontal and vertical velocities, and temperature profiles are illustrated in Figures 2-8. Moreover, the numerical values of the skin friction ![]() (wall shear stress) and rate of heat transfer
(wall shear stress) and rate of heat transfer ![]() are tabulated in Tables 4-11, for different values of parameters of interest.
are tabulated in Tables 4-11, for different values of parameters of interest.
4.1. The Horizontal Velocity
Figure 2 illustrates the effect of ![]() on the profile of the horizontal velocity
on the profile of the horizontal velocity![]() . It is noted that, the horizontal velocity decreases as
. It is noted that, the horizontal velocity decreases as ![]() increases both for
increases both for ![]() (hydrodynamic fluid) and
(hydrodynamic fluid) and ![]() (hydromagnetic fluid) but this decreasing is smaller with
(hydromagnetic fluid) but this decreasing is smaller with ![]() compared with the case
compared with the case![]() , that is because the magnetic force acts as a resistance to the flow, [13] . Also, the boundary layer thickness decreases by increasing
, that is because the magnetic force acts as a resistance to the flow, [13] . Also, the boundary layer thickness decreases by increasing ![]() and the flow makes the stretching surface rougher.
and the flow makes the stretching surface rougher.
Figure 3 describes the effect of ![]() on the behavior of the horizontal velocity
on the behavior of the horizontal velocity![]() . As seen, by increasing the magnetic field, the horizontal velocity and the thickness of the boundary layer decrease. From Figure 3(a) we can conclude that, for
. As seen, by increasing the magnetic field, the horizontal velocity and the thickness of the boundary layer decrease. From Figure 3(a) we can conclude that, for ![]() with small values of
with small values of ![]() less than 0.4 near the surface, the behavior of the horizontal velocity is differ from the well-known cases, that is because the horizontal velocity increases to a maximum values before it starts to decrease.
less than 0.4 near the surface, the behavior of the horizontal velocity is differ from the well-known cases, that is because the horizontal velocity increases to a maximum values before it starts to decrease.
4.2. The Vertical Velocity
Figure 4 shows the behaviour of the vertical velocity ![]() for
for![]() , over a range of the magnetic parameter
, over a range of the magnetic parameter![]() . As seen, the absolute value of the vertical velocity increases with the decrease of
. As seen, the absolute value of the vertical velocity increases with the decrease of![]() .
.
Figure 5 illustrates the behaviour of the vertical velocity ![]() for
for ![]() over a range of the parameter
over a range of the parameter![]() . As seen, the absolute value of the vertical velocity increases with the increase of
. As seen, the absolute value of the vertical velocity increases with the increase of![]() .
.
4.3. The Temperature
Figure 6 illustrates the variation of the temperature profiles ![]() for
for ![]() with Prandtl number
with Prandtl number![]() , over a range of
, over a range of![]() . We notice that, the temperature profiles increases as
. We notice that, the temperature profiles increases as ![]() increases.
increases.
Figure 7 describes the distribution of the temperature ![]() for
for ![]() with
with![]() , over a range of the nonlinear stretching parameter
, over a range of the nonlinear stretching parameter![]() . As seen, with an increase in
. As seen, with an increase in![]() , the temperature increases.
, the temperature increases.
Figure 8 shows the variation of the temperature profiles ![]() for
for ![]() with
with![]() , over a range of the Prandtl number
, over a range of the Prandtl number![]() . As seen, the temperature decreases as the Prandtl number increases which consistent with the fact that the thermal boundary layer thickness decreases as the Prandtl number
. As seen, the temperature decreases as the Prandtl number increases which consistent with the fact that the thermal boundary layer thickness decreases as the Prandtl number ![]() increases.
increases.
4.4. Wall Shear Stress
The dimensionless wall shear stress ![]() (skin friction) is computed for different values of the Hartmann number
(skin friction) is computed for different values of the Hartmann number ![]() and the parameter
and the parameter![]() . Table 4 shows the numerical values of the skin friction
. Table 4 shows the numerical values of the skin friction ![]() for different values of the nonlinear stretching parameter
for different values of the nonlinear stretching parameter ![]() with
with![]() . As seen, the absolute value of the dimensionless wall shear stress
. As seen, the absolute value of the dimensionless wall shear stress ![]() increases with increasing
increases with increasing![]() , that is because by increasing the values of
, that is because by increasing the values of ![]()
the layer thickness decreases with an increase in the skin friction at the wall which may cause to lose the smoothness of the stretching wall. So, by increasing the value of![]() , the flow makes the stretching surface rougher. An excellent agreement between our work and other works is absorbed.
, the flow makes the stretching surface rougher. An excellent agreement between our work and other works is absorbed.
Tables 5-8 show the numerical values of ![]() over a range of
over a range of ![]() with at
with at ![]() and
and![]() , respectively. As
, respectively. As ![]() increases, the absolute value of the dimensionless wall shear stress
increases, the absolute value of the dimensionless wall shear stress ![]() increases and the thickness of the boundary layer decreases. From Table 8, we noticed that, for small values of
increases and the thickness of the boundary layer decreases. From Table 8, we noticed that, for small values of ![]() less than 0.4,
less than 0.4, ![]() decreases as
decreases as ![]() increases which is consistent with Figure 3(a). Again, an excellent agreement is achieved between our work and other works. No convergent value for
increases which is consistent with Figure 3(a). Again, an excellent agreement is achieved between our work and other works. No convergent value for ![]() is obtained by Hayat et al. [9] when
is obtained by Hayat et al. [9] when ![]() at
at![]() , see Table 8.
, see Table 8.
4.5. Wall Shear Stress
Table 9 illustrates the numerical values of the surface heat flux ![]() for different values of the Prandtl number
for different values of the Prandtl number ![]() and nonlinear stretching parameter
and nonlinear stretching parameter ![]() with
with![]() . The thickness of thermal boundary layer becomes thinner when
. The thickness of thermal boundary layer becomes thinner when ![]() increases and this causes an increase in the gradient of the temperature, so, the surface heat flux
increases and this causes an increase in the gradient of the temperature, so, the surface heat flux ![]() increases as
increases as ![]() increases. As seen, the results of the present work are in very good agreement with other works, Table 9.
increases. As seen, the results of the present work are in very good agreement with other works, Table 9.
Also, from Table 9, it is noticed that, for fixed value of![]() , the surface heat flux
, the surface heat flux ![]() decreases as nonlinear stretching parameter
decreases as nonlinear stretching parameter ![]() increases. Also, the value of
increases. Also, the value of ![]() is positive which is consistent with the fact that the heat flows from the sheet surface to the fluid as long as
is positive which is consistent with the fact that the heat flows from the sheet surface to the fluid as long as![]() .
.
Another comparison between the present work with the work of Vajravelu [6] is made, see Table 10.
Table 11 illustrates the numerical values of the surface heat flux ![]() for different values of the
for different values of the ![]() with
with ![]() and
and![]() . As seen, the surface heat flux
. As seen, the surface heat flux ![]() decreases as
decreases as ![]() increases.
increases.
5. Conclusion
We have used Lie-group method to obtain the similarity reductions of the MHD boundary-layer equations. By determining the transformation group under which the given system of partial differential equations and its boundary conditions are invariant, we obtained the invariants and the symmetries of these equations. In turn, we used these invariants and symmetries to determine the similarity variables that reduced the number of independent variables. The resulting system of ordinary differential equations was solved numerically using shooting method coupled with Runge-Kutta scheme and the results were plotted. The numerical values of the wall shear stress (skin friction) and surface heat flux were compared with those obtained by other works and they were found in a good agreement.
Acknowledgements
The author would like to express his appreciations for the potential reviewers for their valuable comments that improved the paper and enhanced the results.