Evaluation of the Impact of Truck Overloading on Flexible Compacted Gravel Lateritic Soil’s Pavements by FEM with Cast3M© ()
1. Introduction
The regulation number 14/2005/CM/UEMOA of WAEMU (West African Economic and Monetary Union) of December 16th, 2005 concerning the harmonization of standards and control procedures of truck volumes, weights and axle loads of heavy goods vehicles in the member states of the Union, set the axle load to 12 tons for a single axle with dual-wheels (Uemoa, 2005 [1] ). However, recent studies showed that this recommended official load is far from being respected. Indeed, 60% - 70% of heavy trucks are overloaded and have significant contribution in the degradation of roads. The objective of this study is to determine the critical response parameters of lateritic roads materials submitted to various conditions of axle overload. The standard axle load is 130 kN (13 tons) for a single axle with dual-wheels (Bceom-Cebtp, 1984 [2] ). The reference load is uniformly distributed on two circles whose centers are from 37.5 cm away from each other. The calculation of the stresses and the strains is done for a typical load of 6.5 tons exercising a vertical pressure q uniformly distributed on two circles with: a = 12.5 cm; l = 3 × a = 37.5 cm and q = 6.62 bars. The reference load for the calculations is represented by the Figure 1.
The reference axle is varied from 13 to 20 tons to take into account the overloading. The effect of a single wheel is tested with a tire pressure of 0.662 MPa for the load of 13 tons and respectively 0.764 MPa, 0.917 MPa and 1.019 MPa respectively for axle loads of the 15, 18 and 20 tons (Samb, 2014 [3] ).
2. Geometry, Materials and Algorithm of Calculations
The structure consists of a 80 mm thick bituminous concrete, a 200 mm thick base layer of lateritic gravels treated or not, a 250 mm thick subbase of untreated lateritic gravels and of a sandy subgrade of infinite thickness. The materials of the asphalt and subgrade layer are considered linear elastic. The base and the subbase has a nonlinear elastic behavior. To take into account this non-linearity, the elastic modulus is replaced by a resilient modulus which depends on the stress level. Several formulations were suggested by using various terms of stresses (Lekarp, Isacsson, and Dawson, 2000 [4] ; Kim, 2007 [5] ) and showed that the models proposed by Uzan (1985) [6] and the NCHRP (2004) [7] allow to take into account the behavior of granular soils as well as fine soils. Triaxial test results on the gravel lateritic soils of Ngoundiane showed that Uzan model give the best correlations and so, the model parameters was determined for these soils.
The Uzan model expresses the resilient modulus according to the bulk stress and the deviatoric stress, which allows us to take into account the effect of the shear behavior:
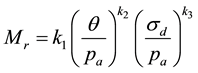 (1)
(1)
with,
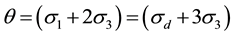 = bulk stress;
= bulk stress;
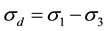 = deviatoric stress;
= deviatoric stress;
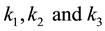 : model parameters.
: model parameters.
For the Young modulus, the maximal values of the unconfined compression tests are chosen, by considering that the gravel lateritic soils are perfectly compacted in 95% of the Optimum Modified Proctor (OMP). For the asphalt layer and the subgrade (Young modulus (E) and Poisson’s ratio (ν)), these values are chosen in reference to Fall, Senghor and Lakhoune (2002) [8] . The materials parameters are given in Table 1. The horizontal movements are blocked in the transverse directions (flexible boundary) and the vertical and horizontal movements are blocked in the bottom of the subgrade (stiff boundary).
For nonlinear analysis, an incremental iterative procedure is used, the tangent constitutive matrix is updated after and during each load increment (NCHRP, 2004). For this implementation, a direct incremental method of the resilient modulus with very small time steps is used. A first test showed that, for the linear method, 24 time-steps were sufficient to reach a constant result. Besides, for the nonlinear model, the tests showed that the
![]()
Figure 1. Schematization of the loading.
results vary very widely according to the compulsory number of steps. From 300 steps, the values stabilize, which explains that the value of the number of steps n was set to these aforesaid values. For every interval of load, the resilient modulus is given with the average of the values found for two successive stages. This algorithm is summarized in Figure 2.
![]()
Table 1. Characteristics of the axisymmetric linear and nonlinear models for the lateritic gravel soils of Ngoundiane (Samb, 2014 [3] ).
![]()
Figure 2. Calculation algorithm used in Cast3M© (Samb, 2014 [3] ).
Impact of Overloading on the Deflection and the Vertical Strain of the Subgrade
The effect of overloading was studied with regard to the normalized axle load of calculation (13 tons). Figure 3(a) and Figure 3(b) and Figure 4(a) and Figure 4(b) give the variation of deflections and strains for the linear and nonlinear models. The results show a linear variation of the axle overload for both models. This proves that it is possible to know in advance the impact of the axle overload on deflections and strains of the pavement layers. We notice that the values of strains and deflections decrease according to the depth. Indeed, the values noticed at the subgrade are lower than those noticed for the other layers.
On the other hand, the impact of the axle overload seems to have more effect on deflection at the top layers (asphalt layer and base layer) than for the lower layers. It is necessary to note that the effect of a single wheel was tested. To know the total deflection and strain, it is necessary to take into account the effect of the dual- wheels. Besides, the variation of deflection and deformation for a variation of the axle overload of 1, 2, 3, 5 and 10 tons is given for the linear model (Table 2). These results show the possibilities of forecasting the response parameters values by analyzing loading scenarios. For a calculated estimation, Table 3 gives a comparison of
![]()
![]() (a) (b)
(a) (b)
Figure 3. Variation of deflections and strains of the pavement layers (in absolute value) of the load for the 2D linear model: (a) Deflections; (b) Strains (Samb, 2014 [3] ).
![]()
![]() (a) (b)
(a) (b)
Figure 4. Variation of deflections and strains of the pavement layers (in absolute value) of the load for the 2D nonlinear model: (a) Deflections; (b) Strains (Samb, 2014 [3] ).
![]()
Table 2. Deflections and deformations caused by the pressure of a tire by tons of axle overload for the linear model and for respectively: 2, 3, 5 and 10 tons (Samb, 2014 [3] ).
Notations: BB: asphalt layer; CB: base layer; CF: subbase layer.
![]()
Table 3. Variation of the critical response due to the pressure of a tire by tons of road overload (Samb, 2014 [3] ).
the variation of deflections and strains for the linear and nonlinear models by tons of axle overload. We can thus notice that the linear model gives higher strain and deflection variations and lower stress variations than for the nonlinear model.
3. Conclusion
The results show a linear variation of deflections and deformations at the road layers according to the variation of the axle overload. This overload seems to have more effects on deflections for the top layers level (asphalt layer and base layer) than the lower layers. It is however necessary to note that the effect of a single wheel is tested. To know total deflections and deformations, it is necessary to take into account the dual tires. These results reveal the possibility of obtaining the response values of roads by analyzing real scenarios of load as well as forecasting the impact of the axle overload on deflections and deformations of road pavements.