New Modeling for Generation of Normal and Abnormal Heart Rate Variability Signals ()
1. Introduction
According to the electrical activity of the heart and considering that the heart produces a series of electrical potentials, these electrical signals of the heart can be recorded by installing electrodes on the chest, left hand, and on the right foot as well. This type of signal is called electrocardiogram or ECG. Figure 1 shows an ECG signal.
Components of this signal are: P, Q, R, S and T. The R component is considered as the component with am- plitude greater than the other components. If we could extract the peak of R by adopting a suitable method, this peak would represent a heartbeat. If the time between successive extracted R peaks is plotted as a function of time, we can have a diagram like the one in Figure 2 which is called the signal of heart beats (heart rate). By using the HR signal vector, we can result in a new signal called Heart Rate Variability (HRV) as Figure 3 and Figure 4.
This research is carried out based on modeling of biological signals. Thus, HRV signals can be synthetically produced by mathematical equations that are used as input for the IPFM model. Hence, this project is performed via modeling and analyzing mathematical relations. This method was chosen because by changing the inputs of IPFM model we can produce synthetic HRV signal which is similar to natural signals (the one taken from human body), and we can model several types of diseases that show their effect on the signal. So it can be concluded that this model is a comprehensive model for generating synthetic HRV signal because it is capable of producing several types of HRV signals. Hence, this type of study and its implementation is considered applied. This research requires several sequences of chaotic signals which can be obtained via relations and initial conditions of the existing resources. In this study, Guyton’s physiology book can be used as the reference to know the function and physiology of the heart and all the nerves of the sympathetic and parasympathetic effects on cardiac signals
2. Review of Previous Research
Jafarnia Dabanloo et al. in 2004 [1] proposed a model based on RBF neural network to produce ECG signal synthetically. The results of this study suggested a low error in producing natural signals. This research was proposed by using a neural network with radial basis functions (RBF) in a nonlinear dynamical model, with the advantage that simulation was performed on a wide range of physiological signals. Finally, the accuracy of the model was evaluated by the introduced error function. The mean of error during 100 seconds by using 20 neurons was less than 2.5 for the proposed model.
By applying the Zeeman nonlinear model, Jafarnia Dabanloo et al. (2006) produced HRV signal with a cycle of ECG signals using neural network. In the results of their survey they reported the effects of breathing signals and production of Mayer waves in the power spectrum of the obtained HRV signal [2] .
In another study Jafarnia Dabanloo et al. (2013) presented a model based on IPFM but with random threshold. They used random sequences with normal distribution [3] .
In a research by Bailon et al. (2011), to produce HRV signal a method based on IPFM was introduced. Time threshold used in this study included non-static values. The proposed method is based on the estimation of produced signals which are dependent on autonomic nervous system using methods from IPFM model with fixed
![]()
Figure 4. Power spectrum density of HRV signal for a healthy person with three peaks that called VLF, LF (Mayer), HF (RSA) [4] .
threshold and this case demonstrates the need for a fixed time-dependent amount to produce signals of the heart rate. Finally, it was shown that the results of this method matched with the values obtained from physiological signals of human body [5] .
In a research, by using physiological IPFM model, Seydnejad et al. [6] obtained physiological data of human body. Most of the methods mentioned in this research focused on low-pass filters to access the modulated signals. In this study, a new method based on the theory of vector space was presented. This new method is based on time-varying uses of IPMF model (TVTIPMF). This model analyzes signals obtained from TVTIPMF as series based on special functions. Then, the matrices obtained from input signals can be used to solve equations in parametric form. In a particular case, applications of this method are used to produce R-R series obtained from SA node to evaluate peripheral nerve functions and the effect of stress.
In 2011, Michele Orini et al. was presented two different methods for producing HRV signals with controlled characteristics and structure of time-frequency (TF) for use in non-stationary HRV analysis [7] . This signal is a random process that TF structure by selecting the time period corresponding to the frequency of the moment, and can either be determined by the shape of the TF function. This method consists of three steps: 1) Select the structure of TF in signal by selecting a set of design parameters; 2) The automatic detection parameters of the model; 3) Synthesis of random signals. Also two measurements for the proper assessment of simulated signals are conducted. They used this framework to model a wide variety of non-stationarities in the modulated heart rate signal during stress test and were effects of music on emotion of human. Proposed model was used for ac- cess to the smoothing distribution pseudo Wigner-Ville distribution (SPWVD) to pattern of HRV [7] .
In 2012, Ali Almasi et al. were presented a dynamic model to generate synthetic Phonocardiogram signals [8] . This model was based on the PCG morphology and consists of three differential equations and can be produce several type of normal PCG signal. Bit to bit PCG change is important in shape of this signal, therefore parameters of model should be have some variety to generate it. This model is inspired of dynamical model to generated electrocardiogram signal that proposed by McSharry et al., and can be used for biomedical signal processing techniques [8] .
In 2013, Diego Martin et al. were presented a stochastic model for Photoplethysmogram (PPG) signal [9] . In that paper, a model of chaotic Photoplethysmographic signal which is able to synthesize and analyze number of other statistical signals was presented. For this purpose, the pulse signal was process to normalization of pulse in time domain. In the next step, a single-pulse-model that consist ten parameters was designed. In third step, time variation in this vector of ten parameters can be approximated by autoregressive moving average models. Application of this model after decorrelation stage that is allows parallel process of each element in the vector. PPG signals were used in this study [9] is 76 signals that 26 of these signals were received by the Omicron FT Surveyor device. In all signals, 5 minutes with is sampling period Ts = 15 ms (Fs = 66.6 Hz), and the signal detected by an optical sensor attached to the right index finger of the samples, and this record were detected in relaxation conditions. Experimental results show that the proposed model is able to preserve the main features of the reference signal. This is reach by linear spectral analysis and also by comparison of the two measurements obtained from nonlinear analysis. The proposed model can be summarized as follows: 1) Tracking of physical activity; 2) Obtain static clinical parameters by the model samples; 3) Recover of lost or missing signals [9] .
In this paper, without taking electrocardiogram signal from human body (and then obtaining HRV signal from it), this signal was obtained through a proposed mathematical model. Various signals derived from the output of this model can be used for final analysis of the HRV signals such as arrhythmia detection and classification of ECG. One application of a dynamic model which is able to produce synthetic ECG signals is the easy evaluation of diagnostic ECG signal processing devices. Such a model can also be used in signal compression and telemedicine. The overall objective of this article is to achieve an applied mathematical model for modeling and synthesizing HR and HRV signals using IPFM model in which chaotic maps are considered as its threshold level.
3. Materials and Methods
3.1. Introduction
In this paper, a mathematical model for synthesizing heart rate variation signals (HRV) has been proposed. In the proposed model, the effect of sympathetic and parasympathetic nerves, and also, an internal input to the SA node that all of which are effective in HRV signals are evaluated. First the input of IPFM model is considered as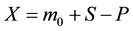 . X is entered in the integrator of IPFM model, and then its integral is calculated. Then this output amount of integrator is compared with chaotic threshold level that had been produced by chaotic maps before. At the end the s (t) output in the model is characterized as the heart rate signal. From this heart rate signal we can reach the heart rate variation signal. In this paper chaotic maps including Logistic Map, Henon Map, Lorenz Map, and Tent Map have been used. Then we also obtain some linear features and frequency range of signal to show that the obtained signal is similar to the normal and natural samples taken from healthy human beings. Now we can claim that the HRV signal obtained from the output of IPFM model is accurate and com- plies with the normal sample.
. X is entered in the integrator of IPFM model, and then its integral is calculated. Then this output amount of integrator is compared with chaotic threshold level that had been produced by chaotic maps before. At the end the s (t) output in the model is characterized as the heart rate signal. From this heart rate signal we can reach the heart rate variation signal. In this paper chaotic maps including Logistic Map, Henon Map, Lorenz Map, and Tent Map have been used. Then we also obtain some linear features and frequency range of signal to show that the obtained signal is similar to the normal and natural samples taken from healthy human beings. Now we can claim that the HRV signal obtained from the output of IPFM model is accurate and com- plies with the normal sample.
3.2. Introducing Chaotic Maps That Used in This Research
This section represents the method of generating chaotic maps used in the present study.
3.2.1. Logistic Map
Equation (1) is called the function of logistic map which is widely used today in modeling especially for natural systems.
 (1)
(1)
Parameter A specifies the chaotic state of this map. This parameter is checked for the state of 0 ≤ x ≤ 1 and 0 ≤ A ≤ 4. At first, the function 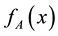 is started with the initial value of
is started with the initial value of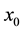 . Then, the amounts of
. Then, the amounts of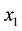 , and
, and 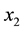 are calculated according to the resulted value.
are calculated according to the resulted value.
The function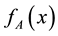 , in fact, depicts a certain amount of 0 ≤ x ≤ 1 (e.g.
, in fact, depicts a certain amount of 0 ≤ x ≤ 1 (e.g.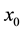 ) to another point of range x (e.g.
) to another point of range x (e.g.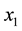 ). This depicting process is repeated in next steps and sequences. If there is such a point, it will be called the fixed point of logistic function. It is clear that as the value of A changes (i.e. the parameter of controlling or changing the environmental effects on the system), several fixed points can be expected or its place will change in the range of x as well. A chain of consecutive values for x that starts from
). This depicting process is repeated in next steps and sequences. If there is such a point, it will be called the fixed point of logistic function. It is clear that as the value of A changes (i.e. the parameter of controlling or changing the environmental effects on the system), several fixed points can be expected or its place will change in the range of x as well. A chain of consecutive values for x that starts from 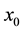 and ends in a fixed value or fixed values is called trajectory and it represents the dynamic behavior of the system. Figure 5 and Figure 6 show the initial curve and bifurcation diagram of a logistic map, respectively.
and ends in a fixed value or fixed values is called trajectory and it represents the dynamic behavior of the system. Figure 5 and Figure 6 show the initial curve and bifurcation diagram of a logistic map, respectively.
![]()
Figure 5. The initial curve of Logistic map.
![]()
Figure 6. The diagram bifurcation of a logistic map. For A < 1 the value z = 0 is an absorbing point. For 1 < A < 3, the fixed point ![]() is the absorbing point. At A = 3, the double period begins and this frequency increase continues. The period greater than 8 times is not clearly distinguished in this figure. Chaos begins at the area that fixed points fill the entire perpendicular line to the A axis randomly.
is the absorbing point. At A = 3, the double period begins and this frequency increase continues. The period greater than 8 times is not clearly distinguished in this figure. Chaos begins at the area that fixed points fill the entire perpendicular line to the A axis randomly.
3.2.2. Lorenz Model
It is a nonlinear system that is a simplified model of convection in the fluids. This model was proposed by meteorologist Edward Lorenz in 1963. Lorenz Model is based on simplification of Navier-Stokes equations for fluids. The fluid motion and temperature disturbances can be mentioned with the three variables X (t), Y (t), and Z (t). These variables are not spatial variables. The variable X is related to the time dependence of the fluid flow function. Variables Y and Z are related to time dependence of temperature deviations in areas far from linear areas of temperature that are obtained for the non-convective mode. By using these variables, the equations of Lo- renz Model can be expressed as three interdependent differential equations as follows (Equation (2)).
![]() (2)
(2)
In the first equation, ![]() expresses the derivative of variable X with respect to time. Parameters P, r and b are adjustable parameters. The parameter P is called the Prandtl number which is defined as the ratio of kinetic viscosity of the fluid to its thermal diffusion coefficient. The parameter r is proportional to the Rayleigh number which is dependent on the measurement of the temperature differences between the upper and lower layers of the fluid. With increasing temperature differences, this number will increase. The parameter b corresponds to the vertical height h of the fluid layer and equals to horizontal convective flows and the value of this parameter in the Lorenz model number is usually equal to 8.3. The value of the parameter p is considered to be 10 which corresponds cold water. In this model, the parameter r is considered as adjustable control parameter.
expresses the derivative of variable X with respect to time. Parameters P, r and b are adjustable parameters. The parameter P is called the Prandtl number which is defined as the ratio of kinetic viscosity of the fluid to its thermal diffusion coefficient. The parameter r is proportional to the Rayleigh number which is dependent on the measurement of the temperature differences between the upper and lower layers of the fluid. With increasing temperature differences, this number will increase. The parameter b corresponds to the vertical height h of the fluid layer and equals to horizontal convective flows and the value of this parameter in the Lorenz model number is usually equal to 8.3. The value of the parameter p is considered to be 10 which corresponds cold water. In this model, the parameter r is considered as adjustable control parameter.
3.2.3. Henon Map
Henon map is a two variables map which is defined by Equation (3).
![]()
![]() (3)
(3)
The diagram in Figure 7 shows the attractor of Henon map according to the parameters a = 1.4 and b = 0.3.
3.2.4. Tent Map
Tent map was defined based on Equation (4).
![]()
Figure 7. Diagram of Henon map attractor.
![]() (4)
(4)
The bifurcation diagram of tent map has been show in Figure 8.
3.3. Human Normal ECG Signal
In this section we introduce a normal ECG signal and how we read it in MATLAB software. The initial calling signal was gained as Figure 9.
In the following figure, the first 10 seconds of ECG signal have been drawn for seeing more clearly (see Fig- ure 10).
![]()
Figure 8. Bifurcation diagram of tent map.
![]()
Figure 10. The first 10 seconds of initial ECG signal.
Then, to have a clean signal, noise deviation from the baseline, AC noise (power) and frequency interference were eliminated by applying the linear filters. Figure 11 shows the conversion of original ECG signal to clean ECG signal. This figure indicates the removal operation of DC component from Original ECG signal.
Also, Figure 12 shows the removing operation baseline noise and the power noise of the original ECG signal. Now we have clean ECG signal (see Figure 13).
After performing the above operations, the R peak of the ECG signal can be extracted. Figure 14 shows the result of extracting the R peak of the ECG signal.
Then, according to the intervals of these extracted peaks, HR and the HRV (from the time difference between the peaks of the extracted R waves) are obtained from the HR. Figure 15 represents the two signals of HR and resulted HRV for normal ECG signal.
Then, the density of power spectrum of the obtained HRV signal is calculated and it is represented in the output. Figure 16 shows the obtained density of power spectrum of the obtained which is consistent with the previous normal samples [2] [3] [6] [10] .
3.4. Proposed Method
3.4.1. Chaotic Maps Used in Proposed Model
In the proposed model we first produce the desired chaotic maps with respect to relations and descriptions set forth in Section 3.2. In this scheme, the chaotic maps including Logistic, Henon, Lorenz, and Tent were used. After coding each formula of these chaotic maps, the output of each chaotic map was saved in a separate matrix.
1) Logistic Map
Logistic map is defined with the initial value of x0 = 0.1, and a matrix sequence and the values obtained from the model can be finally saved in a matrix. To generate chaotic sequence by logistic mapping, the following equation was used. In this case, the initial value x (0) was set to 0.1. A is the control parameter that should be a positive, real and as 0 ≤ A ≤ 4. If the Logistic mapping equation is generated by above relation in which A = 1.2, the system will be stable. If this quantity goes up to 3.57, the system will be chaotic.
2) Henon Map
Henon map was produced based on the Equation (4). Initial values x (0) and y (0) were set to 0.0239 and 0.0239, respectively. The chaotic parameters “a” and “b” were set 1.4 and 0.3, respectively. Then, by using these values and these relations, the chaotic sequence was obtained. The values resulted from the chaotic sequences were saved until they could be used as a threshold in IPFM model.
3) Lorenz Map
Lorenz maps were produced by Equation (2). We’ll check and calculate the fixed points of this model. In
proposed model, the 0.3 as the initial value for x (0) and y (0) and z (0) and values of p = 10, r = 11 and ![]()
![]()
Figure 11. The tow diagrams above: Initial ECG signals with frequency spectrum; the tow diagrams below: The operation of removing the DC component of the ECG signal with its frequency spectrum.
![]()
Figure 12. Tow diagram above: Removing operation of the baseline deviation from ECG signal with its frequency spectrum; Tow diagrams below: The removing operation of the power noise from ECG signal with its frequency spectrum.
![]()
Figure 14. ECG signal with extracted R peaks.
have been allocated to the parameters of the Lorenz model. In the results chapter, the outputs of Lorenz model are shown.
4) Tent Map
![]()
Figure 15. Above: HR signal obtained from ECG signal; Below: HRV signal obtained from normal HR signal.
![]()
Figure 16. HR signal, HRV signal and power spectrum density of the HRV signal obtained from a sample normal ECG signal.
Tent map was produced by Equation (5). In the proposed model, the initial value for xn of this mapping was considered 0.05 and this mapping can be defined as a sequel to 1000 entries. The parameter “a” was also defined in the range of 0 to 1. As a result, after the values obtained from the chaotic mapping are normalized, they are used as threshold values in the IPFM model.
3.4.2. IPFM Model Used in Proposed Model
Heart Rate (HR) is a signal that controlled by the autonomic nervous system (ANS), and it contains of information about changes and signs of heart activity. ANS has two subsystems, sympathetic nerves and parasympathetic nerves. The HR may be increased by sympathetic activity or decreased by parasympathetic activity [10] . In this study, a mathematical model was proposed to generate artificial HRV signals. In this model, sympathetic and parasympathetic nerves, as well as an internal input to the SA node, all of which are effective in HRV signals are checked. Hence, the sympathetic nervous and parasympathetic nervous have been shown with S, and P respectively. The internal input for SA will be represented by ![]() . In fact, these effects along with the interactions with each other are considered as the input of IPFM model. It should be noted that the influence of the sympathetic nervous are shown with
. In fact, these effects along with the interactions with each other are considered as the input of IPFM model. It should be noted that the influence of the sympathetic nervous are shown with ![]() and the influence in parasympathetic nervous has been indicated with
and the influence in parasympathetic nervous has been indicated with ![]() in the model.
in the model.![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() were considered the sine functions as well. This model is based on the assumption that if there is not sympathetic and parasympathetic activity, sinus node will produce oscillations between 115 to 125 beats per minute [11] . Based on this assumption, the entry m0 will be deemed as an assumed index in this model. In addition, the input S1 produces VLF component in HRV signal. As we know, the VLF is related to peripheral vascular and mechanisms of temperature regulation that have been produced by the sympathetic nervous system [10] . Input P1 and S2 respectively can determine the effectiveness of parasympathetic and sympathetic mechanisms that are related to the pressure sensor (baroreceptory) that appear in the LF (or Mayer) [2] . P2 input is another part of the parasympathetic nervous impact on the heart, which its influence is visible in the power spectrum of HRV signal. This input is due to frequency changes of breathing during inhalation and exhalation. These respiratory changes are effective in the HF (or RSA) related to power spectrum of HRV signal [2] .
were considered the sine functions as well. This model is based on the assumption that if there is not sympathetic and parasympathetic activity, sinus node will produce oscillations between 115 to 125 beats per minute [11] . Based on this assumption, the entry m0 will be deemed as an assumed index in this model. In addition, the input S1 produces VLF component in HRV signal. As we know, the VLF is related to peripheral vascular and mechanisms of temperature regulation that have been produced by the sympathetic nervous system [10] . Input P1 and S2 respectively can determine the effectiveness of parasympathetic and sympathetic mechanisms that are related to the pressure sensor (baroreceptory) that appear in the LF (or Mayer) [2] . P2 input is another part of the parasympathetic nervous impact on the heart, which its influence is visible in the power spectrum of HRV signal. This input is due to frequency changes of breathing during inhalation and exhalation. These respiratory changes are effective in the HF (or RSA) related to power spectrum of HRV signal [2] .
All the above mentioned effects of increasing and decreasing heart rate by sympathetic and parasympathetic nerves have been presented in this model by Equation (5).
![]() (5)
(5)
The input of the IPFM model was considered as ![]() that this value should be always positive. X is set as input to the integrator of IPFM model and according to Equation (6), the integral was calculated.
that this value should be always positive. X is set as input to the integrator of IPFM model and according to Equation (6), the integral was calculated.
![]() (6)
(6)
Then the integrator output with a threshold level that was previously generated by chaotic maps is compared. In fact, every chaotic mapping to an IPFM model is defined as a threshold to be considered in that model. There- fore, IPFM model for different chaotic threshold level, the output will be different. These different outputs are obtained from the output of model as the assimilated different HRV signals of the output. Where the value of the integrator output exceeds the threshold level, a pulse is generated from the IPFM model output that will be considered as a heartbeat. In fact, each pulse represents the occurrence or production of an R wave, which is calculated by Equation (7). Then, the HRV signal is achieved by calculating the difference in time of occurrence of the R wave.
![]() (7)
(7)
Figure 17 and Figure 18 show the block diagram of the IPFM circuit used in this study.
3.4.3. Feature Extraction
In this section, from the all signals linear features such as Median, Mean, Variance, Standard Deviation, Maximum Amplitude, Minimum Amplitude, Amplitude Range and Mode, and non-linear features such as Lyapunov Exponent, Shanon Entropy, log Entropy, Threshold Entropy, sure Entropy and mode Entropy were extracted. This features extraction process was done in order to compare the values of the extracted features with artificial signals generated in this method by which the similarities and accuracy percentage of the proposed model output with the normal ECG signal will be calculated. Table 1 and Table 2 show the values of linear features extracted from the normal HR and HRV signal.
![]()
Figure 17. IPFM model used in the proposed model.
![]()
Figure 18. Overall schematic of the simulated HRV signal generation by the IPFM model.
![]()
Table 1. Linear features extracted from the natural HR signal.
![]()
Table 2. Linear features extracted from the natural HRV signal.
3.4.4. Modeling and Generation of Abnormal HRV Signal
In this paper, tow patient that called high sympathetic Balance and Cardiovascular Autonomy Neuropathy (CAN) which is detected and evaluating by HRV signals were simulated. These signals by changing the values of the some coefficients of the normal simulated signal and with extracted frequency feature from these signals were simulated. To modeling HRV signal for these patients, some coefficients basic equation of IPFM model such as ![]() to
to ![]() and also
and also ![]() to
to ![]() were changed (in Equation (5)). In fact, according to the characteristics of the source of heart disease and considering the terms used in the proposed model, abnormal signals were model.
were changed (in Equation (5)). In fact, according to the characteristics of the source of heart disease and considering the terms used in the proposed model, abnormal signals were model.
For final generation of these abnormal signals, frequency features such as energy of low frequency band (EL), energy of high frequency band (HL), ratio of energy in low frequency band to the energy in high frequency band (EL/EH), ratio of energy in low frequency band to the energy in all frequency band (EL/ET) and ratio of energy in high frequency band to the energy in all frequency band (EH/ET) from abnormal signals were extracted and compared with these extracted values from normal signals.
In case of diseases high sympathetic balance, feature as ratio of energy in low frequency band to the energy in high frequency band (EL/EH) in compared with the same ratio in normal signal should increase at about twice, and also feature as ratio of energy in low frequency band to the energy in all frequency band (EL/ET) in compared with the same ratio in normal signal should increase and finally feature as ratio of energy in high frequency band to the energy in all frequency band (EH/ET) in compared with the same ratio in normal signal should re- main unchanged. Also, for simulation of Cardiovascular Autonomy Neuropathy (CAN) signal, feature as ratio of energy in low frequency band to the energy in high frequency band (EL/EH) in compared with the same ratio in normal signal should has value is close to zero, and feature as ratio of energy in low frequency band to the energy in all frequency band (EL/ET) in compared with the same ratio in normal signal should increase and has value is close to zero, and finally feature as ratio of energy in high frequency band to the energy in all fre- quency band (EH/ET) in compared with the same ratio in normal signal should be show a slight decrease. These proportions and values of characteristics of the diseases in compared with the normal HRV signals based on the physiological changes that cause these diseases are on the cardiovascular system (and subsequent created changes on ECG, HR and HRV signals) were included are calculated (from understanding of References [1] [2] [10] ).
4. Results
First, the output of chaotic maps used in this study is presented. Figure 19 shows the output of Logistic chaotic map.
Figure 20 shows the output of Henon chaotic map.
Figure 21 shows the output of Lorenz chaotic map.
Figure 22 shows the output of Tent chaotic map.
This part represents how the results of X (IPFM model input) in the proposed model were calculated. In the IPEM model, the threshold level obtained from the different chaotic maps is compared with the outputs of IPFM model integrator. If the integrator output is more than threshold level, one pulse will be produced in the output. The pulse time (ti) is in fact the time that R wave occurred in HR. The difference between the times obtained re- sults in the production of HRV signal. The results of the proposed model based on the different chaotic maps have been indicated in Figures 23-27.
After achieving the necessary results of the proposed model, these results will be compared statistically with the results of normal signal. Features from the results of the proposed model such as mean, median, variance, standard deviation, maximum amplitude, minimum amplitude, mode and amplitude range were compared with the normal sample. As a result, the model error and the accuracy of the model were obtained.
Then the above mentioned features were obtained from the simulated HRV signals achieved in the previous stage. This extraction of features is done to compare the features resulted from simulated HRV signals with HRV signal which has been obtained from normal and natural ECG signal to find the similarities and accuracy of output in proposed model with normal and natural ECG signal. Tables 3-10 show the linear features extracted from the simulated HR and HRV signal.
Also, some non-linear features of time series sequence were extracted. These feature are Lyapunov Exponent, Shanon Entropy, log Entropy, Threshold Entropy, sure Entropy and mode Entropy. Figures 28-31 were shown results of these features extracted.
The results of the proposed model and comparing to the results achieved from normal and natural HRV signal showed that the proposed model has a good performance in modeling the HRV signal.
5. Discussions
In this study it has presented an applied mathematical model to generate artificial HRV signal based on IPFM model with using chaotic threshold levels. As a result this project will be performed as model using mathematical analysis. This method has been chosen because by means of changing input of IPFM model, we can produce synthetic HRV signal which is similar to the natural signal (the one taken from human body), and we can also model several types of diseases that show their effects on the signal. Considering that this model is capable of producing several types of HRV signals it can be concluded that it is a comprehensive model for synthesizing this type of signal (with comparison to results of references [1] [2] [10] ). So this study can be considered as an applied study in terms of its type and method.
The results of this study indicated that the proposed model has a qualified functioning and there are a lot of similarities between the signals of this model with HRV ones. In this study, the coupling between the sympathetic and parasympathetic nervous system was not intended, however, we achieved acceptable results. The results were closely correlated with the real data which confirm the effectiveness of the proposed model. Various
![]()
Figure 23. Results of IPFM model output base on threshold level of logistic map. Above figure: HR signal; Below figure: HRV signal.
![]()
Figure 24. Results of IPFM model base on threshold level used Henon map (x sequence). Above figure: HR signal; Below figure: HRV signal.
![]()
Figure 25. Results of IPFM model output base on threshold level of Henon map (y sequence). Above figure: HR signal; Below figure: HRV signal.
signals derived from the output of this model can be used for final analysis of the HRV signals, such as arrhythmia detection and classification of ECG and HRV signals. One of the applications of the proposed model is the easy evaluation of diagnostic ECG signal processing devices. Such a model can also be used in signal compres-
![]()
Figure 26. Results of IPFM model output base on threshold level of Lorenz map. Above figure: HR signal; Below figure: HRV signal.
![]()
Figure 27. Results of IPFM model output base on threshold level of Tent map. Above figure: HR signal; Below figure: HRV signal.
![]()
Table 3. Linear features extracted from simulated HR signal by proposed IPFM model using threshold chaotic level of logistic map.
![]()
Table 4. Linear features extracted from simulated HRV signal by proposed IPFM model using threshold chaotic level of logistic map.
![]()
Table 5. Linear features extracted from simulated HR signal by proposed IPFM model using threshold chaotic level of henon map.
![]()
Table 6. Linear features extracted from simulated HRV signal by proposed IPFM model using threshold chaotic level of henon map.
![]()
Table 7. Linear features extracted from simulated HR signal by proposed IPFM model using threshold chaotic level of lorenz map.
![]()
Table 8. Linear features extracted from simulated HRV signal by proposed IPFM model using threshold chaotic level of lorenz map.
![]()
Table 9. Linear features extracted from simulated HR signal by proposed IPFM model using threshold chaotic level of tent map.
![]()
Table 10. Linear features extracted from simulated HRV signal by proposed IPFM model using threshold chaotic level of tent map.
![]()
Figure 28. Comparison of linear feature extracted from natural HR signal and simulated HR signals with proposed method using logistic map, henon map, Lorenz map and tent map, respectively.
![]()
Figure 29. Comparison of non-linear feature extracted from natural HR signal and simulated HR signals with proposed method using logistic map, henon map, Lorenz map and tent map, respectively.
![]()
Figure 30. Comparison of linear feature extracted from natural HRV signal and simulated HRV signals with proposed method using logistic map, henon map, Lorenz map and tent map, respectively.
![]()
Figure 31. Comparison of non-linear feature extracted from natural HRV signal and simulated HRV signals with proposed method using logistic map, henon map, Lorenz map and tent map, respectively.
sion and telemedicine. The major advantage of this study is simplicity and good performance of the proposed model. Figures 28-31 were shown the comparison of all results in this study. Following charts shown the comparison of all the features extracted from natural signals and the simulated signals with proposed method (See Figures 28-31).
As in Figures 28-31 were clear, linear feature of normal HR signal such as median, mean, max amplitude, min amplitude and mode were nearly to these feature that extracted from all simulated HR signal. Variance, standard deviation and amplitude range are features in all simulated HR signals that not close to natural HR sig- nal. Also, non-linear feature of normal HR signal such as lyapunov exponent, Shanon entropy, log entropy, threshold entropy, sure entropy and norm entropy were very nearly to these feature that extracted from all simu- lated HR signal.
About HRV signal, linear feature of normal HRV signal such as median, mean, variance, standard deviation, max amplitude, min amplitude and mode were nearly to these feature that extracted from all simulated HR signal (except results of lorenz map in max amplitude). Also, non-linear feature of normal HRV signal such as lyapunov exponent and average of all entropy were very nearly to these feature that extracted from all simulated HRV signal. But each of entropy singly (especial Shanon and log entropy), is not very closely to the natural HRV signal. It should be noted that these extracted features was not exist in previous researches and in this paper we extracted these features for showing acceptable results of proposed method with comparison to similar studies.
6. Conclusion
In general we can generate artificial HR and HRV signals that results of this method are very closely with normal HR and HRV signals that obtained from human heart. Various signals derived from the output of this model can be used for final analysis of the HRV signals, such as arrhythmia detection and classification of ECG and HRV signals. One of the applications of the proposed model is the easy evaluation of diagnostic ECG signal processing devices. Such a model can also be used in signal compression and telemedicine. Because signals generated by this model due of the high number of cardiac cycles and low volume of these, they can easily upload them to the internet for educational purposes and produce different models of cardiac signals. Also by changing the coefficients of the parameters in Equation (5), production different normal and patient signals from a prototype model, that this is due to the education mode of these signals.
Acknowledgements
This work was supported by Research Fund of Islamic Azad University, Dezful Branch, under research project: “Application Mathematical Model for Artificial Generation of Heart Rate Variability Using IPFM Model with Chaotic Maps”.