Theoretical and Numerical Study of Stress and Thermo-Optic in Photonic Crystal Fiber Laser in Different Pump Schemes ()
1. Introduction
The superiorities of the conventional solid-state and gas lasers make Yb3+ doped fibers lasers reported [1] -[4] . Recently a new type of the pump schemes with the high brightness semiconductor diode pump laser was studied [5] . And the new type of photonic crystal fibers (PCFs) is attracting increasing interests because of its unique properties such as endlessly single-mode guiding, freedom of dispersion characteristics, and large mode area [6] [7] . We also concentrate on PCFs in which a core doped with Yb3+ surrounded by a lower index cladding, which is, surrounded by an air-clad region, in turn, surrounded by a second lower index cladding index.
By analytical and numerical calculation and using the finite-difference method (FDM), we have determined the expressions of temperature distribution in different regions of the photonic crystal fiber laser (PCF) along the axial and radial directions from the integration of the steady-state heat equation for an isotropic medium. Then we used the expressions previously derived for the temperatures in Regions I, II, III, and IV [8] in the results of the expressions for the stress components (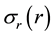 ,
,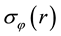 , and
, and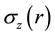 ) and the change in the index of refraction in Regions I, II, III, and IV. The results are compared in different pump schemes for giving the design guidelines to ensure maximum heat dissipation and saving pump powers. The calculated stress values are very small in different pump schemes, and will consequently have a negligible effect upon the index of refraction.
) and the change in the index of refraction in Regions I, II, III, and IV. The results are compared in different pump schemes for giving the design guidelines to ensure maximum heat dissipation and saving pump powers. The calculated stress values are very small in different pump schemes, and will consequently have a negligible effect upon the index of refraction.
The resulting gradients are still small as the corresponding stress values. As a consequence, we expect that changes in the index of refraction due to the stress-optic effect will be negligible in different pump schemes, and thermally induced birefringence will be absent in fiber lasers (in all cases of pumping), the stress component 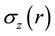 increases with the increase of the length the fiber in the cases (forward pump schemes) and decreases along the fiber laser in the cases (backward pump schemes). These values are between −0.4 ´ 10−6 kg/m2 and −3.4 ´ 10−6 kg/m2 in the four primer cases. Moreover, in the case bi-directional pump scheme, its value is between −0.8 ´ 10−6 kg/m2 and −1.8 ´ 10−6 kg/m2. And the values of the change in index of refraction increases in the cases of forward pump schemes and decreases in the cases of the backward pump schemes, along the fiber laser. For the bi-directional, its value is even smaller.
increases with the increase of the length the fiber in the cases (forward pump schemes) and decreases along the fiber laser in the cases (backward pump schemes). These values are between −0.4 ´ 10−6 kg/m2 and −3.4 ´ 10−6 kg/m2 in the four primer cases. Moreover, in the case bi-directional pump scheme, its value is between −0.8 ´ 10−6 kg/m2 and −1.8 ´ 10−6 kg/m2. And the values of the change in index of refraction increases in the cases of forward pump schemes and decreases in the cases of the backward pump schemes, along the fiber laser. For the bi-directional, its value is even smaller.
2. Average Temperature in PCF
As shown in Figure 1, a typical high power Yb3+-doped double-clad PCF laser consists of an Yb3+-doped dou- ble PCF with reflectors on both of the ends.
Figure 2 shows the heat flow mechanisms in fiber laser and the radial coordinate 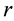 and the tangential angle
and the tangential angle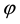 . The quantities
. The quantities 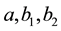 and
and 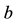 are the core, inner cladding, air-clad and outer cladding radii, respectively.
are the core, inner cladding, air-clad and outer cladding radii, respectively.
![]()
Figure 1. Schematic illustration of end pumped fiber lasers.
![]()
Figure 2. Heat flow mechanisms in PCF laser [9] .
The temperature distribution in a fiber reported in [8] is necessary for determining the radially varying index of refraction due to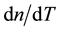 , the calculated stresses, and the change in index of refraction through the stress-optic effect.
, the calculated stresses, and the change in index of refraction through the stress-optic effect.
We calculate the average temperature 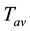 as
as
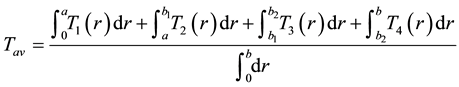 (1)
(1)
where
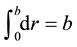 (2)
(2)
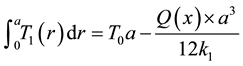 (3)
(3)
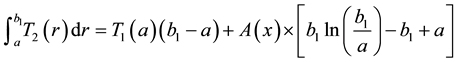 (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where the temperature expressions![]() ,
, ![]() ,
, ![]() and
and ![]() are given by [8] .
are given by [8] .
And
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
3. Stress Distributions
The length of the optical fibers is much greater than a typical fiber outside radius (b), we can invoke the plane- strain approximation [10] in which the z strain everywhere. The radial, tangential, and z stresses![]() ,
, ![]() , and
, and ![]() can be found from [11] .
can be found from [11] .
![]() (10)
(10)
![]() (11)
(11)
in the case where the fiber end faces are free of traction
![]() (12)
(12)
where![]() , E and
, E and ![]() are thermal expansion coefficient, Young’s modulus, and Poisson’s ratio, respectively. So- lution of (10)-(12), using the expressions previously derived for the temperatures in Regions I, II, III, and VI [8] , results in the following final expressions for the stresses in Regions I, II, III, and IV:
are thermal expansion coefficient, Young’s modulus, and Poisson’s ratio, respectively. So- lution of (10)-(12), using the expressions previously derived for the temperatures in Regions I, II, III, and VI [8] , results in the following final expressions for the stresses in Regions I, II, III, and IV:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
where.
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
It can be shown that (13)-(24) satisfy the boundary conditions![]() ,
, ![]() ,
, ![]() , and the continuity conditions
, and the continuity conditions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . Equations (13)-(24)
. Equations (13)-(24)
will be used in Section IV under to calculate the radially varying index of refraction in different pump schemes, due to the stress-optic effect. Note that the equations as derived above for the fiber stresses could also have been obtained by use of the deviation of the temperature distribution from the average and the Airy stress potential [11] .
4. Index of Refractions
Using the expressions for the radial temperature distributions, reported [8] and for the stress distributions (13)- (24), we tray now to make calculation of the radially varying radial and tangential index of refraction distribu- tions. For comparison in different pump schemes, we prefer to cast the calculation of the induced change in the index of refraction in terms of material stresses, rather than strains. We begin by writing the changes in the in- dices of refraction:
![]() (33)
(33)
where
![]() Linear index of refraction;
Linear index of refraction;
![]() Change in index due to change in index with temperature
Change in index due to change in index with temperature![]() ;
;
![]() Stress-induced index changes for the
Stress-induced index changes for the ![]() and
and ![]() components of the electric field.
components of the electric field.
As before, the roman numerals refer to Regions I, II, III and IV. Here, we will calculate ![]() using the following equation:
using the following equation:
![]() (34)
(34)
For Regions I, II, III and IV, becomes
![]() (35)
(35)
And
![]() (36)
(36)
And
![]() (37)
(37)
And
![]() (38)
(38)
The calculation of the stress-induced index changes ![]() are treated in [10] .
are treated in [10] .
Using
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
where ![]() and
and ![]() are the parallel and perpendicular stress-optic coefficients. Their values are
are the parallel and perpendicular stress-optic coefficients. Their values are![]() ,
, ![]() respectively [11] . The numerical values of
respectively [11] . The numerical values of ![]() and
and ![]() are
are ![]() and
and ![]() [12] .
[12] .
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
We can also define the brief ringence![]() , given by
, given by
![]() (55)
(55)
Which may be calculated by using, yielding
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
![]() (59)
(59)
Equations (56)-(59) show that the fiber birefringence depends only on the thermally induced stresses. Finally, by using (43)-(50) and substituting (13)-(20) for the radial, tangential, and ![]() stress components, we arrive at the final equations describing the radially varying indices of refraction in a fiber.
stress components, we arrive at the final equations describing the radially varying indices of refraction in a fiber.
Where ![]() and
and![]() , apart from a constant term, vary quadratically with the fiber radius, in agree- ment with previously published work on bulk rod laser amplifiers [13] [14] . For Region II, however, it is noted that
, apart from a constant term, vary quadratically with the fiber radius, in agree- ment with previously published work on bulk rod laser amplifiers [13] [14] . For Region II, however, it is noted that ![]() and
and ![]() vary in a complicated way that involves both a logarithmic function and an inverse square.
vary in a complicated way that involves both a logarithmic function and an inverse square.
5. Discussions
For simplicity, we concentrated in this work on Yb3+. The core region is surrounded by a circle inner cladding region with dimensions of radius 125 µm, the width of air-clad is 5 µm and which is in turn surrounded by a polymeric outer cladding region with outside diameter of about 300 µm.
5.1. Stress Effect
In Figures 3(a)-(e), we plotted the stress components radial, tangential and longitudinal as a function of the radial coordinate r in different pump schemes for a Yb3+ fiber with a pump of 200 W, b = 300 µm is the outer radius, convective coefficient h = 40.9 W/cm×K. The quantities ![]() and
and ![]() are known in the optics and laser literature as the perpendicular and parallel stress-optic coefficients their values are found in Section 4, the thermal expansion coefficient is
are known in the optics and laser literature as the perpendicular and parallel stress-optic coefficients their values are found in Section 4, the thermal expansion coefficient is ![]() [15] , we show no difference between (a) and (b) in side of the pumping (left side). Moreover, a small difference in other side (side right), we show the same thing for (c) and (d) figures. However, in Figure 3(e) the value of stress is smaller than the previous cases. The difference between the maximum and minimum values of stress components, in the four previous cases (a, b, c, d) is in the order
[15] , we show no difference between (a) and (b) in side of the pumping (left side). Moreover, a small difference in other side (side right), we show the same thing for (c) and (d) figures. However, in Figure 3(e) the value of stress is smaller than the previous cases. The difference between the maximum and minimum values of stress components, in the four previous cases (a, b, c, d) is in the order ![]() but in bi-directional pump scheme Figure 3(e) the value is the order
but in bi-directional pump scheme Figure 3(e) the value is the order![]() . Therefore in bi-directional pump scheme the effects of the stress is negligible with regard to the others cases.
. Therefore in bi-directional pump scheme the effects of the stress is negligible with regard to the others cases.
For more clarification, we plotted the stress components as a function of the radius in different pump schemes. In Figures 4(a)-(e), we observe that there is a rapid increase in air-clad region of the components radial ![]() and longitudinal
and longitudinal![]() . However, concerning the tangential component
. However, concerning the tangential component![]() , the increase is less rapid. We notice that the required boundary conditions are all satisfied. At r = b, the tangential
, the increase is less rapid. We notice that the required boundary conditions are all satisfied. At r = b, the tangential ![]() and longitudinal
and longitudinal ![]() stresses are equal while the radial
stresses are equal while the radial ![]() stress is zero along the fiber. Therefore, we anticipate that changes in the index of refraction due to the stress optic effect will be negligible in all cases of pumping and precisely in bi-directional pump scheme and thermally induced birefringence to be absent in fiber lasers.
stress is zero along the fiber. Therefore, we anticipate that changes in the index of refraction due to the stress optic effect will be negligible in all cases of pumping and precisely in bi-directional pump scheme and thermally induced birefringence to be absent in fiber lasers.
5.2. Index of Refraction
Using (47)-(54), we plotted the tangential and the radial indices of refraction as a function of the radial coordinate r in different pump schemes, Figures 5(a)-(e), the pump power used is 200 W, the fiber outside radius is b = 300 µm, and the convection coefficient is h = 40.9 W/m×K, and ![]() [12] . The curves for
[12] . The curves for ![]()
and ![]() are essentially identical in r = 0 µm and in r = b, and the radially varying index is due to
are essentially identical in r = 0 µm and in r = b, and the radially varying index is due to
![]() only, because
only, because ![]() and
and ![]() are so small. The values of the change in index of refraction de-
are so small. The values of the change in index of refraction de-
crease along the fiber lasers in Figure 5(a) and Figure 5(b) from the order 1.2 × 10−3 to 0.1 × 10−3. In Figure 5(c) and Figure 5(d) the values of change in index of refraction increase in the opposite order 0.1 × 10−3 to 1.2 × 10−3. Nevertheless, in Figure 5(e) the value is in order of 3 × 10−3 to 7 × 10−3. As result, we notice in side of
pumping there is a small difference of the change in index of refraction between the fiber core r = 0 and in the outer clad r = b, the four Figures 5(a)-(d). However, in Figure 5(e) the difference of the change in index of re- fraction between the fiber core r = 0 and in the outer clad r = b is small along the fiber.
6. Summary
In this paper, we have investigated a comparison of stress and thermo-optic of photonic crystal fiber (PCFs) in different pump schemes. Using in these calculations a simple model of (PCFs) and finite differential method (FDM), we have revealed the temperature in the core of the fiber and by laws of heat transfer, we determined its value at the surface of the fiber and the stress value in the different regions of the fiber.
In summary, regarding stress, thermo-optic and the change in index of refraction, their value does not have a great effect on the quality of the laser beam in different pump schemes, especially in the case of the bi-direc- tional pumping. Hence, after this investigation, we proved the architecture of laser cavity that was the most convenient in specific condition. The bi-directional pump scheme is the most suitable because it has less thermal effects than the other cases. However, the backward pump with reflection of 98% and the forward pump with reflection of 98% save more energy than the backward pump with reflection of 0%, the forward pump with ref- lection of 0% and bi-directional pump scheme.