An Electrostatic Catastrophe Machine as an Attosecond Pulse Generator ()
1. Introduction
Since the advent of the laser in 1960, there has been a sustained interest in the quest of generating laser pulses of the shortest duration and of the maximum power. A pulse is the packet of monochromatic waves and the central frequency of the packet is the so-called carrier frequency of the pulse. Thus, there is a fundamental physical limit of duration of a pulse. It is the period of its carrier frequency. The pulse whose duration is of the order of the period of its carrier frequency is called the ultrashort pulse.
In the visible range of the electro-magnetic spectrum, the ultra short laser pulse can have femtosecond durations (1 fs = 10−15 s). Such laser pulses can be directly produced by modern mode-locked lasers [1] [2] . By using the technique of chirped pulse amplification [3] - [8] the power of the femtosecond pulse can be brought up to the Petawatt level (1 PW = 1015W). Focusing with parabolic mirrors [9] allows getting the intensity of this pulse at the target about 1022 W/cm2, which corresponds to the electric field with the strength well above the interatomic electric field (about several volts per angstrom, 109 V/cm).
The so-called attosecond (1 as = 10−18 s) pulse can be created only in the EUV regions of the spectrum. However, in these spectral regions the mode-locking method and the chirped pulse amplification method are no longer applicable.
Fortunately, there are the so-called “catastrophe machines” which transform smooth changes of the input signal into a quick change of their states [10] - [14] . As an example, the “gravitational catastrophe machine” invented by T. Poston [10] [11] can be considered. In this machine the center of gravity is represented as a small heavy ball in a gravitational potential well. The ball takes a position that gives a local minimum of its potential energy. Let the initial potential well have a single minimum, but slowly changing under an external influence of this potential well. In this case a second local potential minimum appears near the first one. This way the second local potential minimum gradually goes down and the first minimum goes up. In the moment the first minimum disappears, the ball jumps to the second potential minimum. This jump is called a “catastrophe”.
The heavy ball in the gravitational potential well can be replaced by an electron in the electrostatic potential well and the external influence by an electric field of a femtosecond laser pulse. In the same way we can create an “electrostatic catastrophe machine” in which the electron jumps from one local minimum with high energy to another one with lower energy. If the difference of the energy levels is of the order of tens of electron volt, the electron jump is accompanied by emission of attosecond electromagnetic pulse in the ultraviolet range of spectrum.
The aim of the article is to explain the work of the hypothetical electrostatic generator of attosecond pulses from the point of view of the catastrophe theory and classical mechanics, and to use the obtained concepts for a quantum description of the real (quantum) electrostatic generator of attosecond pulses.
2. The hypothetical attosecond electromagnetic pulses generator
Let’s consider a classical particle with an elementary charge in a potential well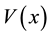 , where
, where 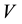 is an electric potential (in volts) at the point
is an electric potential (in volts) at the point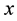 . Assume that the shape of the potential well is described by a biquadratic equation
. Assume that the shape of the potential well is described by a biquadratic equation
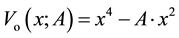 , (1)
, (1)
where 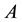 is a parameter. This potential well has a mirror symmetry. If
is a parameter. This potential well has a mirror symmetry. If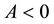 , then the well has a minimum at
, then the well has a minimum at
point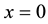 , and if
, and if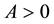 , then it has minima at two points
, then it has minima at two points 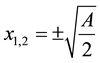 with values
with values 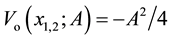
and a maximum at the point 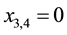 with the value of
with the value of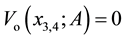 . Thus, in case
. Thus, in case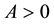 , the potential well
, the potential well
has a W-shaped profile with two minima at points “ “ и “
“ и “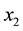 “, separated by a potential barrier with the height of
“, separated by a potential barrier with the height of 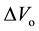 (Figure 1(a)):
(Figure 1(a)):
![]() . (2)
. (2)
Since the distance between the minima (i.e. the width of the potential barrier)
![]() (3)
(3)
is proportional to the square root of the parameter![]() , the height of the potential barrier
, the height of the potential barrier ![]() is associated with the distance between the minima
is associated with the distance between the minima ![]() by the formula
by the formula
![]() . (4)
. (4)
If we add the potential of the electric field of the laser pulse with the maximum strength ![]() (in the form of a linear function
(in the form of a linear function![]() ) to the initial
) to the initial ![]() -shaped potential function, the resulting function takes the form (Figure 1(b))
-shaped potential function, the resulting function takes the form (Figure 1(b))
![]() (5)
(5)
and its potential minima will be redistributed.
The state of the system (a classical particle with elementary charge in a potential well) is described by the in-
ternal variable ![]() and the control variables
and the control variables ![]() and
and![]() :
:![]() . We assume that the evolution of the sys-
. We assume that the evolution of the sys-
tem is quasistatic or adiabatic. When the control variables ![]() and
and ![]() have fixed values, the system settles into
have fixed values, the system settles into
an equilibrium state where the internal variable ![]() minimizes (locally) the function
minimizes (locally) the function![]() :
:
![]() , (6)
, (6)
where
![]() . (7)
. (7)
Combining (6) and (7) one gets the equation of equilibrium states
![]() . (8)
. (8)
Equation (8) gives a surface ![]() in the three-dimensional space with coordinates
in the three-dimensional space with coordinates ![]() which is the so-called catastrophes surface (Figure 2). The surface
which is the so-called catastrophes surface (Figure 2). The surface ![]() divides
divides ![]() -space into two regions. In the region located generally higher than
-space into two regions. In the region located generally higher than ![]() we have
we have![]() . In the region located generally below
. In the region located generally below ![]() we have
we have![]() .
.
Let the ![]() -axis be vertical to the plane of control variables
-axis be vertical to the plane of control variables![]() . The solutions of Equation (8) can be found by drawing a vertical line passing through the point
. The solutions of Equation (8) can be found by drawing a vertical line passing through the point ![]() of the control plane. The line intersects the surface
of the control plane. The line intersects the surface ![]() at the points
at the points![]() , where
, where ![]() is the desired solution. As the catastrophes surface
is the desired solution. As the catastrophes surface ![]() has a fold, the number of solutions based on the parameters
has a fold, the number of solutions based on the parameters ![]() may be equal to 1, 2 or 3 (Figure 2).
may be equal to 1, 2 or 3 (Figure 2).
Minima of the function ![]() are achieved at those values of
are achieved at those values of ![]() for which the function
for which the function ![]() changes its sign from minus to plus. Therefore, the case when equation (5) has one solution corresponds to a minimum of the potential well. When it has three solutions, the middle solution corresponds to the maximum. When it has two solutions, one solution is not the minimum or the maximum, but the second solution is the minimum. At the points of the double solution the vertical line touches the surface
changes its sign from minus to plus. Therefore, the case when equation (5) has one solution corresponds to a minimum of the potential well. When it has three solutions, the middle solution corresponds to the maximum. When it has two solutions, one solution is not the minimum or the maximum, but the second solution is the minimum. At the points of the double solution the vertical line touches the surface![]() , so if one looks from the top at the surface
, so if one looks from the top at the surface![]() , one can see a “visible path”
, one can see a “visible path” ![]() along which the surface bends (Figure 2). This path
along which the surface bends (Figure 2). This path ![]() in the
in the ![]() -plane is called the discriminant set of
-plane is called the discriminant set of![]() . This set separates the points
. This set separates the points ![]() of the control plane giving one solution to
of the control plane giving one solution to ![]() (“outside”
(“outside”![]() ) from those giving three solutions (“inside”
) from those giving three solutions (“inside”![]() ) (Figure 3).
) (Figure 3).
Thus, if the control variables ![]() vary, the catastrophe can happen: the charged particle can jump suddenly from the high local potential minimum to the lower one (This jump is accompanied by the emission of electromagnetic radiation). In this case the moment of the catastrophe is determined by the principle of maximum delay [13] : the state of the system is determined by the local minimum until it exists.
vary, the catastrophe can happen: the charged particle can jump suddenly from the high local potential minimum to the lower one (This jump is accompanied by the emission of electromagnetic radiation). In this case the moment of the catastrophe is determined by the principle of maximum delay [13] : the state of the system is determined by the local minimum until it exists.
The discriminant set ![]() can be found using the condition that at these points the equation
can be found using the condition that at these points the equation ![]() has a double root, i.e.
has a double root, i.e.![]() . Excluding the variable x from the corresponding equations
. Excluding the variable x from the corresponding equations
![]() (9)
(9)
![]() , (10)
, (10)
we obtain![]() :
:
![]() . (11)
. (11)
The generation of ultrashort pulses is a process when ![]() is constant and
is constant and ![]() is a function of time
is a function of time![]() . Let
. Let
![]() , then the discriminant set
, then the discriminant set ![]() degenerates into two points
degenerates into two points ![]() (point “2” in
(point “2” in
![]()
Figure 3. The discriminant set on the control plane.
Figure 3) and ![]() (point “−2” in Figure 3). If
(point “−2” in Figure 3). If![]() , then there is only the right potential
, then there is only the right potential
local minimum (point “−3” in Figure 3), if![]() , then there are two potential local minima (points “−1”, “0”, “1” in Figures 3), and if
, then there are two potential local minima (points “−1”, “0”, “1” in Figures 3), and if![]() , there is only the left potential local minimum (point “3” in Figure 3).
, there is only the left potential local minimum (point “3” in Figure 3).
Let a femtosecond laser produce an ultra short laser pulse in the form of two big oscillations and the amplitude of the first (positive) oscillation is bigger than ![]() and the amplitude of the second (negative) oscillation is smaller than
and the amplitude of the second (negative) oscillation is smaller than ![]() (Figure 4). On the attosecond time scale, the femptosecond pulse can be considered quasistatic.
(Figure 4). On the attosecond time scale, the femptosecond pulse can be considered quasistatic.
If the quasistatic laser pulse falls on the system “the charged particle in the second potential well”, we have a generation of ultrashort pulses which are described by a four-stroke cycle (Figure 5).
Stroke 1 The leading edge of the positive oscillation raises the charged particle in the second potential minimum
until this potential well disappears. During this time interval, the particle reserves the energy![]() .
.
Stroke 2 According to the principle of maximum delay, in the moment when the positive amplitude of the leading edge equals ![]() the second potential well disappears and a catastrophe occurs: the charged particle jumps from the high second minimum
the second potential well disappears and a catastrophe occurs: the charged particle jumps from the high second minimum ![]() to the low first minimum
to the low first minimum ![]() and radiates an attosecond
and radiates an attosecond
pulse with a carrier frequency of![]() .
.
Stroke 3 The leading edge of the negative oscillation raises the charged particle in the first potential mini-
mum until the potential well disappears. During this time interval the particle reserves the energy![]() .
.
![]()
Figure 5. The four-stroke cycle of the hypothetical attosecond generator.
Stroke 4 According to the principle of maximum delay, in the moment when the negative amplitude of the leading edge equals ![]() the first potential well disappears and a catastrophe occurs: the charged particle jumps from the high first minimum
the first potential well disappears and a catastrophe occurs: the charged particle jumps from the high first minimum ![]() to the low second minimum
to the low second minimum ![]() and radiates an attosecond pulse with a carrier frequency of
and radiates an attosecond pulse with a carrier frequency of![]() .
.
At the end of the fourth stroke the system returns to its initial state and the cycle can be repeated. Thus, if this catastrophe machine could exist in nature, it would be a perfect attosecond pulse generator.
3. The real attosecond electromagnetic pulses generator
There is a real generation of attosecond pulses in which an electric field of a focused extremely powerful femtosecond pulse interacts with a valence electron in the potential well of the noble gas atom [15] - [17] . Note that the work of a real generator of attosecond pulses can be explained by using the concepts of the hypothetical generator of attosecond pulses and the so-called semi classical approximation of quantum mechanics.
According to de Broglie, electrons have wave properties. An electron is described by a wave function. The wave function has a wave length![]() . In semi classical Bohr model of the atom (1913), valence electrons rotate in circular stationary orbits around the atom nucleus [18] . The stationary orbit satisfies the standing wave condition: the whole number of the electron wavelengths l must fit along the circumference of the orbit [18] :
. In semi classical Bohr model of the atom (1913), valence electrons rotate in circular stationary orbits around the atom nucleus [18] . The stationary orbit satisfies the standing wave condition: the whole number of the electron wavelengths l must fit along the circumference of the orbit [18] :
![]() , (12)
, (12)
where ![]() is an integer,
is an integer, ![]() is the radius of the
is the radius of the ![]() -orbit. In this case the energy level of the electron in the
-orbit. In this case the energy level of the electron in the ![]() - orbit (the so-called ionization energy [19] ) is
- orbit (the so-called ionization energy [19] ) is
![]() , (13)
, (13)
where ![]() is the effective nuclear charge [20] . In contrast to the classical particle with an elementary charge, an electron doesn’t lie at the bottom of the electrostatic potential well, but lies at the n-th energy level
is the effective nuclear charge [20] . In contrast to the classical particle with an elementary charge, an electron doesn’t lie at the bottom of the electrostatic potential well, but lies at the n-th energy level![]() .
.
Let the atom be illuminated by a focused femtosecond powerful laser pulse. If the strength ![]() of the electric field of the laser pulse is close the strength of the Coulomb field of the atom nucleus, the resulting potential well for the valence electron becomes a superposition of the Coulomb potential well and the linear function
of the electric field of the laser pulse is close the strength of the Coulomb field of the atom nucleus, the resulting potential well for the valence electron becomes a superposition of the Coulomb potential well and the linear function ![]() (in volts) [21] :
(in volts) [21] :
![]() , (14)
, (14)
where ![]() is the charge of the electron,
is the charge of the electron, ![]() is Coulomb’s constant. Note that the resulting potential
is Coulomb’s constant. Note that the resulting potential![]() , equation (14), has the potential barrier with the height
, equation (14), has the potential barrier with the height ![]() (see Figure 6). The width of the barrier is determined by the distance between the turning points
(see Figure 6). The width of the barrier is determined by the distance between the turning points ![]() and
and![]() , where the potential
, where the potential ![]() is equal to the basic energy level ?
is equal to the basic energy level ?![]() :
:
![]() . (15)
. (15)
The quadratic equation with respect to ![]()
![]() (16)
(16)
gives two solutions:
![]() (17a)
(17a)
is the left turning point (a particle from the region I falls into the region II),
![]() (17b)
(17b)
is the right turning point (a particle from the region II falls into the region III).
For further calculations it is necessary to choose a simple criterion of the barrier width at which the electron tunnels through the barrier. The condition of the stationary orbit, equation (12), and the condition for tunneling (the width of the barrier is comparable to the wavelength of the electron![]() ) allow us to formulate a simple criterion: the electron tunnels through the barrier if the barrier width equals the diameter of the stationary orbit divided by
) allow us to formulate a simple criterion: the electron tunnels through the barrier if the barrier width equals the diameter of the stationary orbit divided by ![]() (points “−2” and “2” in Figure 7). Note that this criterion can be written in the arithmetic form as
(points “−2” and “2” in Figure 7). Note that this criterion can be written in the arithmetic form as
![]()
Figure 7. The tunneling curve on the control plane.
![]() . (18)
. (18)
![]() . (19)
. (19)
The generation of ultrashort pulses is a process when ![]() is constant and
is constant and ![]() is a function of time
is a function of time![]() , as we
, as we
can see in Figure 7. Let![]() , then the tunneling curve
, then the tunneling curve ![]() degenerates into two points:
degenerates into two points:
![]() (point “2” in Figure 7) and
(point “2” in Figure 7) and ![]() (point “−2” in Figure 7). If
(point “−2” in Figure 7). If![]() ,
,
then tunneling is not impossible (points “−1”, “0”, “1” in Figure 7). If ![]() , then the left potential barrier can be tunneled by the electron (point “−2” in Figure 7) and if
, then the left potential barrier can be tunneled by the electron (point “−2” in Figure 7) and if![]() , the right potential barrier can be tunneled by the electron (point “2” in Figure 7).
, the right potential barrier can be tunneled by the electron (point “2” in Figure 7).
Let a femtosecond laser produce an ultrashort laser pulse in the form of two oscillations where the amplitude of the first (positive) oscillation is bigger than ![]() and the amplitude of the second (negative) oscillation is smaller than
and the amplitude of the second (negative) oscillation is smaller than ![]() (Figure 4). On an attosecond time scale, the femtosecond pulse can be considered as quasistatic.
(Figure 4). On an attosecond time scale, the femtosecond pulse can be considered as quasistatic.
According to Keldysh [22] [23] , the process of tunneling ionization of the valence electron is “quasistatic” too, if the carrier frequency of the laser pulse ![]() is significantly less than the frequency of an electron
is significantly less than the frequency of an electron ![]() tunneling through the potential barrier
tunneling through the potential barrier
![]() ,
,
where![]() ,
, ![]() and
and ![]() are the charge, mass and energy of the electron, and
are the charge, mass and energy of the electron, and ![]() is the maximum amplitude of the laser pulse.
is the maximum amplitude of the laser pulse.
If a quasistatic laser pulse falls on a quasistatic system “electron in the potential well of the atom nucleus”, we have the generation of ultrashort pulses which is described by a six-stroke cycle (Figure 8).
Stroke 2 When the electric strength ![]() reduces from
reduces from ![]() to 0, the electron reserves the energy
to 0, the electron reserves the energy
![]() .
.
Stroke 3 When the electric strength ![]() equals 0, the potential barrier disappears and, according to the principle of maximum delay, a catastrophe occurs: the electron jumps from the zero energy level to the basic energy
equals 0, the potential barrier disappears and, according to the principle of maximum delay, a catastrophe occurs: the electron jumps from the zero energy level to the basic energy
level and radiates an attosecond pulse with a carrier frequency of![]() .
.
Figure 8. The six-stroke cycle of the real attosecond generator.
Stroke 5 When the electric strength ![]() increases from
increases from ![]() to 0, the electron reserves the energy
to 0, the electron reserves the energy
![]()
Stroke 6 When the electric strength ![]() equals 0, the potential barrier disappears and, according to the principle of maximum delay, a catastrophe occurs: the electron jumps from the zero energy level to the basic energy
equals 0, the potential barrier disappears and, according to the principle of maximum delay, a catastrophe occurs: the electron jumps from the zero energy level to the basic energy
level and radiates an attosecond pulse with a carrier frequency![]() .
.
At the end of the sixth stroke the system returns to its initial state and the cycle can be repeated.
In the table of the elements there is a periodic trend for ionization energy [19] : each period begins at a minimum for the alkali metals, and ends at a maximum for the noble gases. So, to generate attosecond pulses the hydrogen or the noble gases are used. As the H ionization energy [19] is 13.59 eV, He―24.58 eV, Ne―21.56 eV, Ar―15.76 eV, Kr―13.99 eV, Xe―12.13 eV, Hg―10.43 eV, Rn―10.74 eV, the corresponding radiation refers to the soft EUV region of the spectrum. The duration of the ultra short pulse in a photon energy range of 10 eV to 25 eV cannot be less than 100 as.
In the catastrophe theory the principle of maximum delay is widely used [13] . In this article we have used this principle too. However, it does not allow taking into account the kinetic energy of an electron oscillating in an external laser field the so-called ponder motive energy. To produce the hard EUV-rays or even X-rays ponder motive energy must be taken into account. In this case, the principle of maximum deceleration should be replaced by a different, more suitable principle.
4. Conclusion
The transformation from the input femtosecond pulse in the visible spectrum to the output attosecond pulse in the ultraviolet spectrum is a transformation of a smooth changing input signal to a quickly changing output signal, so it is a field of interest of the catastrophe theory. We propose a criterion for tunneling (18) and a quasiclassical model of the transformation of femtosecond laser pulses into attosecond pulses described as an electrostatic catastrophe machine.