1. Background
Virtually all modern theories of elasticity [1] - [4] build the equations to describe elasticity using stress and/or strain. Hardy [5] proposed to return to the approach of Euler, Lagrange, and Poisson [6] to build the equations of elasticity using point locations and forces instead of stress and strain. Hardy called these equations the equations of Euler-Lagrange elasticity. The equations of Euler-Lagrange elasticity are appropriate for quasi-static defor- mations, but do not include dynamics. Dynamics will be added in this paper.
Hardy defined an elastic material as one which when deformed, stores energy; and when it is returned to its original state, the stored energy is returned to its surroundings. This is known as hyper-elasticity [7] . Hardy followed the notation of Spencer [8] by defining the initial position of each point in an elastic material to be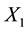 ,
, 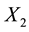 , and
, and  corresponding to the x, y, and z coordinates of that point. The parameters,
corresponding to the x, y, and z coordinates of that point. The parameters, 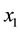 ,
, 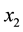 ,
,  were defined as the x, y, z coordinates of the corresponding point after the deformation. The final position of each point depends upon the initial position, so that each component of each point,
were defined as the x, y, z coordinates of the corresponding point after the deformation. The final position of each point depends upon the initial position, so that each component of each point,  , is a function of
, is a function of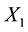 ,
, 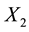 , and
, and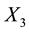 . The energy of the material is a function of the final positions of each point
. The energy of the material is a function of the final positions of each point  (i = 1, 2, 3) and the
(i = 1, 2, 3) and the
relative change in distances between points, 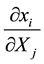 (i and j = 1, 2, 3). This energy is expressed in terms of the energy per unit original volume,
(i and j = 1, 2, 3). This energy is expressed in terms of the energy per unit original volume, 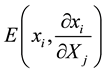 , which can be divided into the energy associated with body forces,
, which can be divided into the energy associated with body forces, 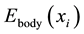 , plus the energy associated with the deformation of the body,
, plus the energy associated with the deformation of the body, 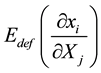 ,
,
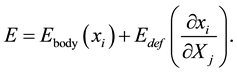 (1)
(1)
To obtain the Euler-Lagrange differential equations, Hardy minimized the total energy, ![]() ,
,
![]() , (2)
, (2)
which resulted in three Euler equations,
![]() (3)
(3)
The advantage of Hardy’s approach is that Equation (3) is applicable to both infinitesimal and finite defor- mations as well as being appropriate for both anisotropic and isotropic materials. The disadvantage of this approach is that it is only appropriate for quasi-static deformations, since time dependence is not included. In this paper, I will extend this approach to include dynamics.
2. Adding Dynamics
To add dynamics to the Euler-Lagrange elasticity equations several changes are needed to the quasi-static approach. First define each ![]() as a function of time as well as
as a function of time as well as![]() ,
, ![]() , and
, and![]() . Second define an appro- priate Lagrangian. Third minimize the integral of the Lagrangian over both space and time. Lagrangians for particle dynamics are defined as the kinetic energy minus the potential energy of the particle. To extend this to a distributed material, our “particle” will be an infinitesimal volume of the elastic material. Define the kinetic energy per original volume of the material as
. Second define an appro- priate Lagrangian. Third minimize the integral of the Lagrangian over both space and time. Lagrangians for particle dynamics are defined as the kinetic energy minus the potential energy of the particle. To extend this to a distributed material, our “particle” will be an infinitesimal volume of the elastic material. Define the kinetic energy per original volume of the material as
![]() , (4)
, (4)
with ![]() the mass per original volume of the material and the velocity of any point in the material,
the mass per original volume of the material and the velocity of any point in the material, ![]() , is
, is
![]() (5)
(5)
Define the potential energy per unit original volume as ![]() in Equation (1) and the Lagrangian,
in Equation (1) and the Lagrangian, ![]() as
as
![]() (6)
(6)
Substitute Equation (1) into Equation (6) with ![]() and T from Equation (4) to express
and T from Equation (4) to express ![]() as
as
![]() (7)
(7)
Now find the extrema of
![]() (8)
(8)
Since![]() , the following three Euler equations result from setting
, the following three Euler equations result from setting![]() :
:
![]() (9)
(9)
Substituting ![]() from Equation (7) gives
from Equation (7) gives
![]() , (10)
, (10)
or
![]() (11)
(11)
Equation (11) are the equations of dynamics for deformation of elastic materials. All that is required is to define ![]() of the material experimentally. The
of the material experimentally. The ![]() must be invariant under coordinate rotations and translations. One method is to define
must be invariant under coordinate rotations and translations. One method is to define ![]() in terms of invariants of the
in terms of invariants of the ![]() matrix (e.g. Ogden [9] , Hardy [10] ).
matrix (e.g. Ogden [9] , Hardy [10] ).
Note that no assumptions of infinitesimal deformation or isotropy have been made to derive Equation (11), so they are applicable for both infinitesimal and finite deformations of both isotropic and anisotropic materials. The most surprising thing about Equation (11) is that each term in Equation (11) can be given a simple physical interpretation.
3. Physical Interpretation of the Terms in Equation (11)
In order to give a physical interpretation to the individual terms in Equation (11) consider a small cuboid defined as![]() . The term on the left hand side of Equation (11),
. The term on the left hand side of Equation (11), ![]() , is the change in momentum per unit original volume of this cuboid with respect to time in the limit as
, is the change in momentum per unit original volume of this cuboid with respect to time in the limit as![]() ,
, ![]() and
and ![]() approach 0. The first term on the right hand side,
approach 0. The first term on the right hand side, ![]() , is the force of gravity per unit original volume of this cuboid in the same limit. The second term on the right hand side,
, is the force of gravity per unit original volume of this cuboid in the same limit. The second term on the right hand side, ![]() , is shown below to be the net surface force per unit original volume applied to all the surfaces of the cuboid as the volume of the cuboid shrinks to zero. In other words, Equation (11) is just an expression of Newton’s laws
, is shown below to be the net surface force per unit original volume applied to all the surfaces of the cuboid as the volume of the cuboid shrinks to zero. In other words, Equation (11) is just an expression of Newton’s laws ![]() for each infinitesimal volume of the material.
for each infinitesimal volume of the material.
To see that ![]() is indeed the net surface force per unit original volume acting on the cuboid, recall that Hardy [5] found that the external force acting on a surface can be written as
is indeed the net surface force per unit original volume acting on the cuboid, recall that Hardy [5] found that the external force acting on a surface can be written as
![]() (12)
(12)
Let ![]() represent a particular plane during deformation, where the magnitude of
represent a particular plane during deformation, where the magnitude of ![]() is the current infinitesimal area of the plane and the direction of
is the current infinitesimal area of the plane and the direction of ![]() is perpendicular to the plane of interest and pointing away from the material receiving the force. To calculate the force on this plane using Equation (12), find the original magnitude and direction of
is perpendicular to the plane of interest and pointing away from the material receiving the force. To calculate the force on this plane using Equation (12), find the original magnitude and direction of ![]() before the deformation. Call this
before the deformation. Call this![]() . Define the components of
. Define the components of ![]() be
be![]() ,
, ![]() , and
, and ![]() in the
in the![]() ,
, ![]() , and
, and ![]() directions respectively. The three components of the force exerted on the
directions respectively. The three components of the force exerted on the ![]() plane at any time during the deformation are then calculated from Equation (12) as
plane at any time during the deformation are then calculated from Equation (12) as
![]() (13)
(13)
For our cuboid, defined as![]() , the
, the ![]() component of the force on a plane of the cuboid originally perpendicular to
component of the force on a plane of the cuboid originally perpendicular to ![]() is
is![]() , where
, where
![]() . (14)
. (14)
For example, ![]() is the
is the ![]() component of the force on plane
component of the force on plane![]() . Divide the body into cuboids along the
. Divide the body into cuboids along the ![]() direction as shown in Figure 1(a). As shown in this figure,
direction as shown in Figure 1(a). As shown in this figure, ![]() is the component of force on region a from region b in the
is the component of force on region a from region b in the ![]() direction.
direction. ![]() is the component of force on region b from region c. If we wish to express the net force on region b alone, this would be
is the component of force on region b from region c. If we wish to express the net force on region b alone, this would be ![]() as shown in Figure 1(b). The net force in the
as shown in Figure 1(b). The net force in the ![]() direction on region b along the
direction on region b along the ![]() direction when divided by the cuboid’s original volume is
direction when divided by the cuboid’s original volume is
![]() (15)
(15)
Taking the limit as the dimensions of the cube go to zero gives the net force per unit original volume on region b in the ![]() direction on the
direction on the ![]() faces of the cube,
faces of the cube, ![]() , to be
, to be
![]() (16)
(16)
A similar argument using ![]() and
and ![]() yields the net forces normal to the
yields the net forces normal to the ![]() and
and ![]() faces,
faces, ![]() and
and![]() , to be
, to be
![]() (a)
(a)![]() (b)
(b)
Figure 1. Force within the material in the X3 direction on the dA3 surfaces (a) internal forces from Equation (14) (b) forces on region b.
![]() , (17)
, (17)
and
![]() (18)
(18)
Next consider![]() . Using Figure 2 and an argument similar to the one used in Figure 1 gives
. Using Figure 2 and an argument similar to the one used in Figure 1 gives
![]() , (19)
, (19)
and in general
![]() (20)
(20)
Combining these results, we have the total force in the ![]() direction to be
direction to be
![]() , (21)
, (21)
for i = 1, 2, 3, and summed over j = 1, 2, 3, which is the third term in Equation (11). Thus ![]()
is the net surface force per unit original volume in the ![]() direction on any cuboid in the limit as the cuboid dimensions shrink to zero.
direction on any cuboid in the limit as the cuboid dimensions shrink to zero.
Figure 3 summarizes this result by illustrating the forces summed in each direction to calculate the net surface force on a cuboid of material. Note that in Figure 3 only the forces on the “front” faces of the cuboid are
![]()
Figure 2. Forces in the X3 direction on the two dA2 faces within the material and on a region.
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 3. Forces in each direction on surfaces of cuboid (forces on the back sides not shown). (a) Surface forces in the X1 direction; (b) Surface forces in the X2 direction; (c) Surface forces in the X3 direction.
shown. There are forces on the rear surfaces that also contribute to each ![]() term.
term.
4. Some Details
The procedure outlined in the last section to calculate the force on a plane after a deformation seems a bit convoluted in that the location of the plane before any deformation must be found in order to find the force on the plane after deformation. However, Equation (12) are excellent for applying Neumann boundary conditions to Equation (11). As an example, consider the case of deforming a rectangular body as shown in Figure 1(a) by applying some force on the ![]() face of the cuboid. If we know the components of the applied force from boundary conditions as a function of time, we can write
face of the cuboid. If we know the components of the applied force from boundary conditions as a function of time, we can write
![]() (22)
(22)
If the force is applied uniformly over the area, ![]() is simply the applied force divided by a constant, the origial area. Therefore the Neumann boundary condition using Equation (12) is defined using just a rescaled version of the applied force on the surface of the material.
is simply the applied force divided by a constant, the origial area. Therefore the Neumann boundary condition using Equation (12) is defined using just a rescaled version of the applied force on the surface of the material.
Finite deformations may displace and distorted planes in the cuboid from their original positions, but as long as inversions are not allowed, the same bounding surfaces of the cuboid are found regardless of how the material is deformed. The values of ![]() change from point to point as the material is deformed, but the
change from point to point as the material is deformed, but the ![]() vectors are unchanged by the deformation. Thus the forces shown in Figures 1-3 may be displaced due to the finite deformation, but the orientation of each component of each force from each surface is the same and the form of the sum of the forces,
vectors are unchanged by the deformation. Thus the forces shown in Figures 1-3 may be displaced due to the finite deformation, but the orientation of each component of each force from each surface is the same and the form of the sum of the forces, ![]() , is unchanged by the displacement.
, is unchanged by the displacement.
Lastly, it is tempting to consider the second order tensor quantity ![]() to be stress, but it is only stress for infinitesimal deformations. This is because
to be stress, but it is only stress for infinitesimal deformations. This is because ![]() must be multiplied by the orignal surface vector, not the current one to get the force at the current location.
must be multiplied by the orignal surface vector, not the current one to get the force at the current location.
5. Conclusion
The equations for dynamics in Euler-Lagrange elasticity have been derived. These equations are shown to be a simple statement of Newton’s Law ![]() for each infinitesimal volume of the material. The derived equations, Equation (11), are applicable to infinitesimal and finite deformations for both isotropic and anisotropic materials.
for each infinitesimal volume of the material. The derived equations, Equation (11), are applicable to infinitesimal and finite deformations for both isotropic and anisotropic materials.