The Calculations of General Relativity on Massive Celestial Bodies Collapsing into Singular Black Holes Are Wrong ()
1. Introduction
S. Chandrasekhar proved in 1935 that the mass of white dwarf has an upper limit, i.e., so-called the Chandrasekhar limit [1] . If the mass exceeds the limit, the celestial body will become unstable and contract into a neutron star further. In this proof, only the Newtonian theory of gravity is used without involving general relativity. In fact, the Newtonian theory of gravity is accurate enough for common celestial bodies. The Einstein’s theory of gravity is unnecessary.
After that, J. R. Oppenheimer proved that the upper limit of neutron star is about 0.75 times of solar mass [2] . If this limit is exceeded, neutron stars become unstable. Though general relativity is used in this proof, it only involves the static equation of gravity field without considering the moving speed of material.
In 1939, Oppenheimer proved further that when the masses are great enough, the celestial bodies would collapse into singular black holes with infinite density [3] . Einstein did not believe this result at first but accepted it at last. The paper of Oppenheimer opened a door for the research of singularity black holes.
The calculation of Oppenheimer about celestial bodies collapsing into singularly black holes is abstruse and hard to understand so that common text books do not introduce it. Most physicists only accept Oppenheimer’s statement but do not understand the details. The author examines the original paper of Oppenheimer recently and finds many mistakes in it. The conclusion of Oppenheimer about celestial bodies collapsing into singularly black holes does not hold at all. The main problems are as follows.
1) The calculation of Oppenheimer hidden a premise, i.e., the density of celestial body was a constant 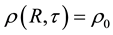 having nothing to do with space-time coordinates. However, the deduced conclusion is that massive celestial body would collapse into singularity with infinite density. The premise and conclusion contradicts each other.
having nothing to do with space-time coordinates. However, the deduced conclusion is that massive celestial body would collapse into singularity with infinite density. The premise and conclusion contradicts each other.
2) There are no any restriction on the initial density and radius for celestial body in the calculation. That is to say, according to Oppenheimer’s calculation, a cloud of thin gas may also collapse into singular black hole under the action of gravity. This is completely impossible.
3) Suppose that 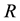 is the radius of celestial body at time
is the radius of celestial body at time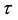 , according to Oppenheimer’s calculation,
, according to Oppenheimer’s calculation, 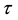 increases with
increases with 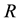 increasing. However, what Oppenheimer discussed was the collapse process of celestial body in which the radius of celestial body should decreases with time
increasing. However, what Oppenheimer discussed was the collapse process of celestial body in which the radius of celestial body should decreases with time 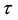 increases. So Oppenheimer’s calculation describes the expansion of celestial body, rather than contraction.
increases. So Oppenheimer’s calculation describes the expansion of celestial body, rather than contraction.
4) There are other obvious mathematical and physical mistakes in Oppenheimer’s calculations.
5) More generally, the calculations of general relativity in this kind of problems have the mistake of procedure. In order to solve the Einstein’s equation of gravity for material collapse, we should know dynamic energy momentum tensor in advance including the forms of material density changing with space-time coordinates. Otherwise the equation of gravity field cannot be solved. Conversely, if we have known the forms of material density changing with space-time coordinates, we can judge directly whether or not massive celestial body collapses. In this case, we do not need to solve the Einstein’s equation of gravity at all. However, in the practical problems of celestial body collapse, we cannot know dynamic energy momentum tensor in advance. So the Einstein’s equation of gravity is actually incapable for this problem.
6) In order to escape this predicament, physicists introduce co-moving coordinates. The observers are assumed to move with material along the radial direction so that the speed of material seems to be canceled. However, observer moving with material is equivalent to falling freely in gravity field. According to the principle of general relativity, gravity field would be eliminated locally and space-time would become flat. In this situation, there is no problem of matter collapsing again.
7) Most celestial bodies in nature have rotating speeds. In the evolution processes of celestial bodies, angle momentums are conservative. For massive celestial bodies, rotating speeds are much greater than radial speeds. Because co-moving coordinate frame moves along the direction of radius, it is impossible using it to describe the real motion of celestial bodies. Due to very high rotating speeds, the final destiny of massive celestial bodies is falling apart, instead of collapsing into singularities. However, the calculations of general relativity completely neglect the rotation speeds of celestial bodies.
8) Another improved method to calculate star’s collapse also has similar problems in which even arbitrary coordinate transformations are used to simplify the motion equations. So the results are also incredible.
In this paper, we first introduce the improved and simplified calculation adopted in Weinberg’s book “Gravity and Cosmology” [4] and points out the mistake in it. Then, we discuss the proof of Oppenheimer. The conclusion is that both improved and Oppenheimer’s calculations have not proved that massive material may collapse into singular black holes.
2. The Improved Calculation on the Collapse of Celestial Body
2.1. The External Solution of Material Sphere
Weinberg’s book discusses the simplest collapsing process of a material sphere in which pressure is neglected. The solutions are divided into both external and inner parts. The metric of gravitational field with spherical symmetry in the external space of sphere is
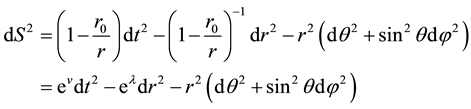 (1)
(1)
Here 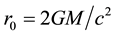 is gravity radius. According to the Birkhoff theorem of general relativity, the gravity field of external space with spherical symmetry is always in the form (1) no matter whether the volume and density of sphere change with time or not.
is gravity radius. According to the Birkhoff theorem of general relativity, the gravity field of external space with spherical symmetry is always in the form (1) no matter whether the volume and density of sphere change with time or not.
2.2. The Inner Solution of Material Sphere
Suppose that the space-time coordinates inner sphere are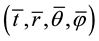 . For the problem of spherical collapsing, the metric is written as [4]
. For the problem of spherical collapsing, the metric is written as [4]
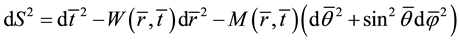 (2)
(2)
If the pressure of fluid is neglected, energy momentum tensor is 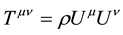 in which
in which 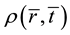 is proper density. When velocities are considered, the co-moving coordinates have to been used. Otherwise the Einstein’s equation of gravity cannot be solved. The rationality of co-moving coordinate will be discussed later. In the co- moving coordinate frame, the four dimensional velocities of a particle are
is proper density. When velocities are considered, the co-moving coordinates have to been used. Otherwise the Einstein’s equation of gravity cannot be solved. The rationality of co-moving coordinate will be discussed later. In the co- moving coordinate frame, the four dimensional velocities of a particle are 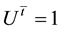 and
and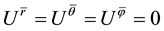 . The formula of momentum conservation is satisfied automatically with
. The formula of momentum conservation is satisfied automatically with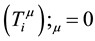 . The formula of energy conservation is
. The formula of energy conservation is
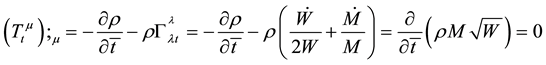 (3)
(3)
The Einstein’s equation of gravity is ![]() in which
in which
![]() (4)
(4)
By considering (2) and (3), the non-zero components are obtained with
![]() (5)
(5)
Substituting (5) in the Einstein’s equation of gravity, we get four formulas below
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Suppose that density has nothing to do with space coordinates with ![]() and set
and set
![]() (10)
(10)
We get ![]() from (9). By introducing coordinate transformation
from (9). By introducing coordinate transformation![]() , the following relation is considered and consider following relation
, the following relation is considered and consider following relation
![]() (11)
(11)
The formula (11) is supposed tenable without proof in the book. Substituting (11) in (10) and cancelling the sign of ripple, the following formulas are obtained
![]() (12)
(12)
Comparing (12) with (10), we know that (11) is equivalent to let ![]() directly. In this way, (7) and (8) can be written as
directly. In this way, (7) and (8) can be written as
![]() (13)
(13)
![]() (14)
(14)
By comparing both formulas above, we get
![]() (15)
(15)
Here ![]() is a constant. The integral of (15) is
is a constant. The integral of (15) is
![]() (16)
(16)
By substituting (12) and (14) in (2), we get at last
![]() (17)
(17)
The formula is actually the Robertson-Walker metric with constant curvature ![]() which is commonly used in cosmology. Substitute (10) in the formula of energy conservation (3), we obtain
which is commonly used in cosmology. Substitute (10) in the formula of energy conservation (3), we obtain![]() . Set
. Set![]() , we have
, we have
![]() (18)
(18)
By considering (12), (15) and (18), the Equations (8) and (14) become
![]() (19)
(19)
![]() (20)
(20)
By cancelling ![]() from both formulas above, we get at last
from both formulas above, we get at last
![]() (21)
(21)
Let ![]() when
when![]() , we have
, we have![]() . The formula (21) becomes
. The formula (21) becomes
![]() (22)
(22)
The solution of (22) can be represented by the parameter equations of cycloid curve
![]() (23)
(23)
When![]() , we have
, we have ![]()
![]() (24)
(24)
It indicates that a fluid sphere without pressure with initial density ![]() may collapse into the state of
may collapse into the state of ![]() in finite time
in finite time ![]() with zero volume and infinite density. That is black hole.
with zero volume and infinite density. That is black hole.
2.3. The Solution in Vacuum outside Sphere and the Boundary Condition
The vacuum solution (1) outside sphere is different from the solution (17) inside the sphere. In order to make the metrics continuous, same transformations have to be introduced so that they have the same forms on the boundary of sphere. However, as Weinberg said in the book, the transformations have something confuse. So we only provide the result here. By introducing following transformations in (17) to set![]() ,
, ![]() ,
, ![]() and
and
![]() (25)
(25)
![]() (26)
(26)
Here constant ![]() is the initial radius of sphere. We write (17) as
is the initial radius of sphere. We write (17) as
![]() (27)
(27)
in which
![]() (28)
(28)
By using co-moving coordinates, the radius of celestial body is ![]() at arbitrary moment. When
at arbitrary moment. When![]() , we have
, we have![]() . So on the surface of celestial body with
. So on the surface of celestial body with![]() , we have
, we have
![]() (29)
(29)
Comparing (27) and (29) with (1), we take
![]() (30)
(30)
In this way, we can make the metric to be continuous on the boundary of sphere. Let ![]() in (1) for light’s motion and taking the integral, we get
in (1) for light’s motion and taking the integral, we get
![]() (31)
(31)
In which ![]() is the time the light emits from star’s surface with radius
is the time the light emits from star’s surface with radius ![]() and
and ![]() is the time the light reaches distance with coordinate
is the time the light reaches distance with coordinate![]() . According (31), when
. According (31), when ![]() or
or![]() , we have
, we have![]() . So if the surface of sphere contracts to the Schwarzschild radius, an infinite time is needed for light emitting from the surface to reach an observer located at the distance place. It is impossible for the observer outside the sphere to see the later process in which the sphere collapse into singularity with
. So if the surface of sphere contracts to the Schwarzschild radius, an infinite time is needed for light emitting from the surface to reach an observer located at the distance place. It is impossible for the observer outside the sphere to see the later process in which the sphere collapse into singularity with![]() .
.
2.4. The Problems Exist in the Calculations Above
1) In the calculation, it is assumed that the density of start has nothing to do with space coordinate with form![]() . However, this precondition cannot hold. According to common understanding, in the quickly contracting process of massive stars, the density of material cannot be uniform.
. However, this precondition cannot hold. According to common understanding, in the quickly contracting process of massive stars, the density of material cannot be uniform.
2) The formula (11) has no any mathematical and physical reason. The simplified formula (12) is only an artificial patchwork, not a rational deduction.
3) According to (24), the time that a celestial body collapses from static state into the state of infinite density is only related to initial density![]() , having nothing to do with celestial body’s mass and original radius. Besides, there is no any limitation for the values of
, having nothing to do with celestial body’s mass and original radius. Besides, there is no any limitation for the values of![]() . Obviously, this is impossible in general situations. Otherwise a cloud of small and thin gas can also collapse into a singularity. For example, the solar average density is
. Obviously, this is impossible in general situations. Otherwise a cloud of small and thin gas can also collapse into a singularity. For example, the solar average density is![]() . According to (24) (taking normal unit to let
. According to (24) (taking normal unit to let![]() ), the sun would collapse into a singularity in
), the sun would collapse into a singularity in ![]() years. However, the sun has been
years. However, the sun has been ![]() years old.
years old.
4) (27) describes the metric inside sphere, so (25) represents the time inside sphere with ![]() and
and ![]() in (26). According to (25), when
in (26). According to (25), when![]() , we have
, we have![]() . It means that it needs infinite time for a star contracting to a radius less than the Schwarzschild radius. That is to say, the Schwarzschild radius is the limitation of material density. Material sphere cannot collapse into a singularity with zero radius and infinite density. The result contradicts with (24).
. It means that it needs infinite time for a star contracting to a radius less than the Schwarzschild radius. That is to say, the Schwarzschild radius is the limitation of material density. Material sphere cannot collapse into a singularity with zero radius and infinite density. The result contradicts with (24).
5) Substituting (15) in (13) and considering (8), we get
![]() (32)
(32)
By cancelling ![]() from the formulas above, we get the Freidman equation of cosmology
from the formulas above, we get the Freidman equation of cosmology
![]() (33)
(33)
However, E. A. Milne proved in 1943 that the Freidman equation can be deduced directly from the Newtonian formula of gravity [5] . The result of improved calculation is equal to say that according to the Newtonian theory, arbitrary celestial body can collapse into singularity! It is certain that something is wrong in the calculations.
6) Because co-moving coordinates are used, the velocities of material are neglected. However, even though observers are at rest in the co-moving coordinate frame, because ![]() changes with time, the relativity velocities between observer and material are still exist. For example, suppose that an observer is rest at the original point of co-moving coordinate frame, the velocity of material located at point
changes with time, the relativity velocities between observer and material are still exist. For example, suppose that an observer is rest at the original point of co-moving coordinate frame, the velocity of material located at point ![]() relative to the observer is
relative to the observer is![]() . So we have to consider material’s momentums in the Einstein’s equation of gravity field. However, the formulas (6)-(10) have not contained material’s momentums.
. So we have to consider material’s momentums in the Einstein’s equation of gravity field. However, the formulas (6)-(10) have not contained material’s momentums.
7) In the co-moving coordinate frame, observers fall freely with material in gravity field. According to the principle of equivalence in general relativity, the local space-time is flat. So it is impossible for us to use (2) and (17) to describe the metric for an observer who is rest at the co-moving coordinate frame.
8) In fact, most celestial bodies in nature have rotating speeds. Especially, for massive celestial bodies, the rotating speeds are much greater than the speeds along the direction of radius. The co-moving coordinate frame moving along the direction of radius cannot describe the real rotations of celestial bodies. For example, for a neutron star with 10 times of solar mass and radius![]() , the tangential speed is
, the tangential speed is ![]() when the star rotates one time within a hundredth of a second. If the neutron star collapses into a singularity in one day, the speed of collapse along the radial direction is
when the star rotates one time within a hundredth of a second. If the neutron star collapses into a singularity in one day, the speed of collapse along the radial direction is![]() , much less than the speed of rotation. Using co- moving coordinates
, much less than the speed of rotation. Using co- moving coordinates ![]() with radius speed
with radius speed ![]() cannot describe the real motion of star’s material. Because of the existences of high rotating speeds, massive celestial bodies will fall apart, rather than collapse into singularities. The calculation of general relativity completely neglect the rotation speeds of celestial bodies, the conclusion of material collapse is suspect.
cannot describe the real motion of star’s material. Because of the existences of high rotating speeds, massive celestial bodies will fall apart, rather than collapse into singularities. The calculation of general relativity completely neglect the rotation speeds of celestial bodies, the conclusion of material collapse is suspect.
9) General relativity uses the Schwarzschild and Kerr solutions to describe static and rotating black holes. Within the horizon, to ensure the square of length being a positive quantity, space coordinate ![]() and time
and time ![]() should exchange each other. In light of common understanding, when celestial body collapses, the radius
should exchange each other. In light of common understanding, when celestial body collapses, the radius ![]() decreases with time
decreases with time ![]() increases. If
increases. If ![]() and
and ![]() exchange within the horizon,
exchange within the horizon, ![]() becomes space coordinate and
becomes space coordinate and ![]() becomes time. In the process of collapse,
becomes time. In the process of collapse, ![]() decreasing means time backflow and
decreasing means time backflow and ![]() increasing means celestial body expanding. So the process of mass collapse becomes that time backflows and celestial body expansion. In (24),
increasing means celestial body expanding. So the process of mass collapse becomes that time backflows and celestial body expansion. In (24), ![]() becomes the final radius of celestial body with initial density
becomes the final radius of celestial body with initial density![]() . For the solar initial density, we have
. For the solar initial density, we have![]() , similar to the radius of a galaxy. The result is obviously absurd.
, similar to the radius of a galaxy. The result is obviously absurd.
3. The Calculation of Oppenheimer
3.1. The External Solution of Sphere
J. R. Oppenheimer considered the collapse process of a sphere with uniform density (Taking ![]() actually.) without pressure. He at first assumed that the density of sphere has nothing to do with coordinates, then assumed that the density of sphere has nothing to do time. Also, He used (1) to describe the gravity field of external sphere.
actually.) without pressure. He at first assumed that the density of sphere has nothing to do with coordinates, then assumed that the density of sphere has nothing to do time. Also, He used (1) to describe the gravity field of external sphere.
3.2. The Inner Solution of Sphere
In the calculation of Oppenheimer, the metric inner sphere is [3]
![]() (34)
(34)
Based on this metric, the Einstein’s equation of gravity field becomes
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
In the formulas, the non-zero components![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() of energy momentum tensor contain velocities, the Equations (34)-(38) are impossible to solve. So Oppenheimer used the substitutive Tolman solution in practical calculation.
of energy momentum tensor contain velocities, the Equations (34)-(38) are impossible to solve. So Oppenheimer used the substitutive Tolman solution in practical calculation.
3.3. The Tolman Solution [6]
The Tolman solution is considered to use the co-moving coordinates too in which the non-zero component of energy momentum tensor is![]() . The other components are zero, meaning that the velocities of material are neglected actually. Then, the metric of gravity field inside the sphere is written as
. The other components are zero, meaning that the velocities of material are neglected actually. Then, the metric of gravity field inside the sphere is written as
![]() (39)
(39)
In (39), ![]() is common space coordinate, instead of scalar factor
is common space coordinate, instead of scalar factor![]() . The Einstein’s equation of gravity field become
. The Einstein’s equation of gravity field become
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
The solution of (43) is
![]() (44)
(44)
In which ![]() is an arbitrary function of
is an arbitrary function of![]() . Substitute (44) in (40) and set
. Substitute (44) in (40) and set![]() , we get
, we get
![]() (45)
(45)
The integral of (45) is
![]() (46)
(46)
Here ![]() and
and ![]() are the arbitrary functions of
are the arbitrary functions of![]() . Substitute (44) in (41), we also get (46). From (42), (44) and (46), we have
. Substitute (44) in (41), we also get (46). From (42), (44) and (46), we have
![]() (47)
(47)
Oppenheimer chosen![]() . At a certain moment for
. At a certain moment for![]() , the density is only the function of
, the density is only the function of ![]() and (47) becomes one order equation of
and (47) becomes one order equation of ![]() with
with
![]() (48)
(48)
It will be pointed out later that (48) is untenable in general situations. After obtaining (48), Oppenheimer thought further that when ![]() was equal to a fixed value, an arbitrary initial value
was equal to a fixed value, an arbitrary initial value ![]() could be chosen so that (48) could be written as
could be chosen so that (48) could be written as
![]() (49)
(49)
Here ![]() is a constant and
is a constant and ![]() is the initial radius of star. A special solution of (49) is
is the initial radius of star. A special solution of (49) is
![]() (50)
(50)
Here ![]() is gravity radius introduced only for convenience. In this way, the metric (39) is determined. In order to make it continuous with the external solution on the surface of sphere, the following coordinate transformations have to be introduced.
is gravity radius introduced only for convenience. In this way, the metric (39) is determined. In order to make it continuous with the external solution on the surface of sphere, the following coordinate transformations have to be introduced.
3.4. The Coordinate Transformation of Tolman Solution
Let ![]() and
and![]() , we have
, we have ![]() and
and![]() . Substitute them in (1) and obtain
. Substitute them in (1) and obtain
![]() (51)
(51)
Comparing (51) with (39), we obtain
![]() (52)
(52)
By considering (44), we get from (52)
![]() (53)
(53)
![]() (54)
(54)
By considering (46) and (52), we have
![]() (55)
(55)
![]() (56)
(56)
From (54), (55) and (56) , we get
![]() (57)
(57)
For the situation with![]() , the common solution is
, the common solution is
![]() (58)
(58)
Here ![]() is the arbitrary function of
is the arbitrary function of ![]() and
and ![]() is determined by (52). For the situation with
is determined by (52). For the situation with![]() , the common solution is
, the common solution is
![]() (59)
(59)
Here ![]() is the arbitrary function of
is the arbitrary function of![]() .
.
3.5. The Boundary Conditions
In the region ![]() outsider sphere, the metric has the form of (1). The form of
outsider sphere, the metric has the form of (1). The form of ![]() can be determined by considering (1). From (58), it takes
can be determined by considering (1). From (58), it takes ![]() or
or![]() . On the surface of sphere with
. On the surface of sphere with![]() , Oppenheimer take
, Oppenheimer take ![]() for any
for any![]() . The form of
. The form of ![]() can be determined by this condition. It is known from (59) to have
can be determined by this condition. It is known from (59) to have ![]() while
while![]() . By considering
. By considering ![]() and using (58), we have
and using (58), we have
![]() (60)
(60)
By using condition![]() , Oppenheimer got
, Oppenheimer got
![]() (61)
(61)
Substitute (61) in (60), the transformations between ![]() and
and![]() , as well as (53) can be determined.
, as well as (53) can be determined.
3.6. The Collapse of Celestial Body
For a great enough time![]() , Oppenheimer obtained from (60)
, Oppenheimer obtained from (60)
![]() (62)
(62)
When ![]() is fixed and
is fixed and![]() ,
, ![]() is a finite value satisfying the relation
is a finite value satisfying the relation
![]() (63)
(63)
It can be obtained from (63)
![]() (64)
(64)
According to Oppenheimer, (64) represents the condition that the observer who moves with material cannot send out a light sign from a star, or light corn is closed so that light sign cannot escape from star. Oppenheimer estimated that for a star with mass ![]() and initial density
and initial density![]() , the time
, the time ![]() was about one day. Substitute (61) and (62) in (53), Oppenheimer obstained
was about one day. Substitute (61) and (62) in (53), Oppenheimer obstained
![]() (65)
(65)
![]() (66)
(66)
Oppenheimer discussed the asymptotic behaviors of (65) and (66). Because the problems revealed below, the discussions become meaningless, so we do not introduce them again.
3.7. The Problems Exist in the Calculations of Oppenheimer
1) It is assumed at first in (48) that density ![]() is unrelated to time, then it is assumed further in (49) that
is unrelated to time, then it is assumed further in (49) that ![]() has nothing to do with space coordinate with
has nothing to do with space coordinate with![]() . However, theses hypotheses have no any reason and are impossible at all! If density does not change with time, how does the radius changes with time and the density become infinite at last? The premise contradicts with the conclusion so that the calculation of Oppenheimer is meaningless completely.
. However, theses hypotheses have no any reason and are impossible at all! If density does not change with time, how does the radius changes with time and the density become infinite at last? The premise contradicts with the conclusion so that the calculation of Oppenheimer is meaningless completely.
2) At a certain moment to have![]() , Oppenheimer obtained (48) from (47). If
, Oppenheimer obtained (48) from (47). If![]() , (48) does not hold. We should still use (48) to describe the process. The reason is that thought
, (48) does not hold. We should still use (48) to describe the process. The reason is that thought ![]() and
and ![]() seem to be independent each other, the Equations (40)-(43) of gravity fields connect them actually. In fact, (47) describes the function relation between
seem to be independent each other, the Equations (40)-(43) of gravity fields connect them actually. In fact, (47) describes the function relation between ![]() and
and![]() . For example, when
. For example, when![]() , we have
, we have
![]() (67)
(67)
Therefore, both (49) and (50) do not hold in general situations when![]() .
.
3) The constant ![]() is considered as gravity radius in (50). However, it is actually an integral constant determined by boundary condition. According to (46) and (50), we cannot declare that
is considered as gravity radius in (50). However, it is actually an integral constant determined by boundary condition. According to (46) and (50), we cannot declare that ![]() is gravity radius. It is only an arbitrary constant with the dimension of length. If
is gravity radius. It is only an arbitrary constant with the dimension of length. If ![]() is not gravity radius, time
is not gravity radius, time ![]() in (64) becomes unrelated to gravity constant and mass and has nothing to do with the collapse process of material. In fact, by connecting (49) and (50), we can determine constant
in (64) becomes unrelated to gravity constant and mass and has nothing to do with the collapse process of material. In fact, by connecting (49) and (50), we can determine constant![]() . However, the integral process of (49) produces another constant. This integral constant can be determined by the boundary condition when
. However, the integral process of (49) produces another constant. This integral constant can be determined by the boundary condition when![]() . Unfortunately, this constant is neglected in the Oppenheimer’s calculation.
. Unfortunately, this constant is neglected in the Oppenheimer’s calculation.
4) According to (50) and (46), in the space outside sphere with![]() , we have
, we have
![]() (68)
(68)
However, the metric is related to time![]() , so it cannot be extended into the space outside sphere according to the Birkhoff theorem. In this way, the calculations after (50) in the space of external sphere become meaningless.
, so it cannot be extended into the space outside sphere according to the Birkhoff theorem. In this way, the calculations after (50) in the space of external sphere become meaningless.
5) In order to know whether or not a star collapse into a singularity in finite time really, we should take the integral of (47), then discuss the relation between ![]() and
and![]() . However, Oppenheimer did not do it. The reason is that
. However, Oppenheimer did not do it. The reason is that ![]() is unknown so that (47) cannot be integrated at all. In this meaning, the Einstein’s equation of gravity cannot be used to calculate celestial body’s collapses. In fact, in order to solve the equation of gravity, we have to know the function relations that a star’s density changes with space-time coordinates in advance, instead of obtaining the relations by solving the equation of gravity. However, if the function relations of density changing with space-time coordinates have been known in advance, we can judge whether or not a star can collapse into a singular black hole immediately. We do not need to solve the equation of gravity again. Therefore, the procedure of calculating material collapse is wrong in general relativity. Only by this point, we can say that Oppenheimer did not prove that a star could collapse into a singular black hole.
is unknown so that (47) cannot be integrated at all. In this meaning, the Einstein’s equation of gravity cannot be used to calculate celestial body’s collapses. In fact, in order to solve the equation of gravity, we have to know the function relations that a star’s density changes with space-time coordinates in advance, instead of obtaining the relations by solving the equation of gravity. However, if the function relations of density changing with space-time coordinates have been known in advance, we can judge whether or not a star can collapse into a singular black hole immediately. We do not need to solve the equation of gravity again. Therefore, the procedure of calculating material collapse is wrong in general relativity. Only by this point, we can say that Oppenheimer did not prove that a star could collapse into a singular black hole.
6) In (64), ![]() is the radius of celestial body at arbitrary moment and time
is the radius of celestial body at arbitrary moment and time ![]() increases with
increases with ![]() increase. However, what Oppenheimer discussed was the collapse of celestial body in which the radius of celestial body should decreases with time
increase. However, what Oppenheimer discussed was the collapse of celestial body in which the radius of celestial body should decreases with time ![]() increases. So, at best, (64) describes the expansion of celestial body, rather than contraction. In fact, Oppenheimer only obtained (62) without deducing (64) and discussing it so that this problem is neglected.
increases. So, at best, (64) describes the expansion of celestial body, rather than contraction. In fact, Oppenheimer only obtained (62) without deducing (64) and discussing it so that this problem is neglected.
7) In the calculations of Oppenheimer, there are no any restriction on the initial values of celestial body’s mass, density and radius. The formulas (62) and (64) are tenable generally even for a cloud of thin gas. That is to say, according to Oppenheimer’s calculation, a cloud of thin gas can also collapse into singular black hole. Regardless of ![]() increase with
increase with ![]() increase, suppose that a common star begins to contract from the initial radius
increase, suppose that a common star begins to contract from the initial radius![]() . In finite time
. In finite time![]() , the radius becomes
, the radius becomes![]() . According to (62), for an observer located outside the star, the time is still infinite with
. According to (62), for an observer located outside the star, the time is still infinite with![]() . That is to say, an observer needs a infinite time to see a star’s radius changing from
. That is to say, an observer needs a infinite time to see a star’s radius changing from ![]() to
to![]() , even though the difference
, even though the difference ![]() and
and ![]() is very small. These results are absurd. We can only say that (62) is meaningless.
is very small. These results are absurd. We can only say that (62) is meaningless.
8) There are other mistakes in Oppenheimer’s paper. For example, it is ![]() rather than
rather than ![]() on the right side of (48). The dimensions are different on the two sides of formula (64). The dimension on the left side is first power of length with
on the right side of (48). The dimensions are different on the two sides of formula (64). The dimension on the left side is first power of length with![]() , but on the right side, the dimension is 3/2 power with
, but on the right side, the dimension is 3/2 power with ![]() (Both
(Both ![]() and
and ![]() are the first power of length). Therefore, (64) cannot be correct.
are the first power of length). Therefore, (64) cannot be correct.
9) The Tolman solution is used practically in the calculation of Oppenheimer. The Tolman solution is considered to be based on co-moving coordinate. However, the real situation is that in the original equation (39), ![]() is normal coordinate rather than co-moving coordinate. As shown in improved calculation, co-moving coordinate should be
is normal coordinate rather than co-moving coordinate. As shown in improved calculation, co-moving coordinate should be![]() . For an observer who is rest at co-moving coordinate frame,
. For an observer who is rest at co-moving coordinate frame, ![]() is unchanged in the contracting process of star. Therefore, (39) is based on static reference frame. There exists relative speed between observer and star’s material and dynamic energy momentum tensors should be considered. However, (40)-(43) do not contain material’s velocities. Theses movement equations are inexplicable. Based on these equations, the calculations of Oppenheimer are certainly wrong at beginning.
is unchanged in the contracting process of star. Therefore, (39) is based on static reference frame. There exists relative speed between observer and star’s material and dynamic energy momentum tensors should be considered. However, (40)-(43) do not contain material’s velocities. Theses movement equations are inexplicable. Based on these equations, the calculations of Oppenheimer are certainly wrong at beginning.
4. Discussions
It can be concluded that the calculations of general relativity about celestial bodies collapsing into singularity black holes are wrong. Based on general relativity, physicists have never successfully proved that material can collapse into singularity up to now. The theories of so-called singular black holes in the astrophysics have no any scientific foundation actually. Before this manuscript, the author has published a series of papers to prove that singular black holes cannot exist in nature [7] [8] . In these papers, the static solutions of Einstein’s equation of gravity are discussed for the material distributions just as hollow sphere, ring and double-spheres and so on. In this paper, the dynamic solutions of Einstein’s equation of gravity are discussed further. It reveals the limitation of Einstein’s theory of gravity more deeply.
In fact, The Einstein’s theory of gravity has never been used successfully in the problems that the material of field source has moving velocity. The reason is that in this case the Einstein’s equation of gravity cannot be solved. In order to solve the equation, physicists have to introduce co-moving coordinates. The purport is to cancel the influence of velocity on the equation of gravity. But it cannot represent the real process of physics. This fact reveals that the Einstein’s equation of gravity is practically invalid when the material of field source has moving velocities.
Therefore, the so-called singular black holes, white holes and wormholes in cosmology and astrophysics have nothing to do with real world. The space-time singularities in general relativity are caused by the description method of curve space-time, rather than massive mass. According to the current understanding, black holes may exist in the centers of quasars. However, according to the observations of Rudolf E. Schild and Darryl J. Leiter, the center of Quasar 0957 + 561 is a close object called as MECO (Massive Eternally Collapsing Object), not a singularity black hole [9] [10] . MECO is surrounded by a strong magnetic field. The observation of Rudolf E. Schild is consistent with the calculation and analyses in this paper. That is to say, if there are black holes in the universal space, they can only be the Newtonian black holes without singularities, not the Einstein’s singularity black holes.
In the modern cosmology based on the Einstein’s theory of gravity, the same problems also exist. By introducing both simplified conditions the co-moving coordinates and the R-W metric, the Freidman equation of cosmology is obtained and used to describe the expansive universe. However, as proved by British Physicist E. A. Milne, the Freidman equation can also be deduced directly from the Newtonian equation of gravity. No any revised item is contained in the Freidman equation. The result indicates that the current cosmology is based on the Newtonian theory of gravity actually. The Freidman equation is only suitable for the universal processes with low expansive speed, unsuitable for the universal processes with high expansive speed just as the high red shift of Ia supernovas. This is the reason why cosmology needs the hypotheses of dark energy, so much non-baryon dark material and accelerating expansion.
On the other hand, by transforming the geodesic equation of the Schwarzschild solution of the Einstein’s equation of gravity field to flat space-time for description, the relativity revised Newtonian formula of gravity can be obtained [11] . Based on it, we can explain the experiments of general relativity well without any space-time singularity. Using this revised formula to describe the expensive universe, the revised Freidman equation can be obtained and the high red shifts of Ia supernovas can also be explained well. We do not need the hypotheses of dark energy, non-baryon dark material and the accelerating universe again. Many fundamental problems in cosmology can be solved thoroughly [12] .
All these tell us that the geometric describing form of gravity is impossible and should be given up. The description of gravity should retune to the normal form of dynamics in flat space-time through the revision of the Newtonian theory.