1. Introduction
Welding process has been widely used in structure fabrication to join materials. However, welding inevitably induces material properties change, residual stress and deformation due to intense localized heating during welding and fast cooling after welding, especially for heat treatment strengthened high strength steels and aluminum alloys. Although post-weld heat treatment (PWHT) can be used to recover the material strength, it is not practical to conduct PWHT for all welds. It is common that welding effects on materials are ignored during designing welded structures. The same material properties as base materials were used in the welding area, which could result in structure failures during service because a softening zone is often formed near a weld of high strength steels and joint strength is typical lower than base materials for heat-treatment strengthened aluminum alloys.
ICME has been gradually used in industries to develop products and produce new alloys [1] - [3] because it creates significant cost benefit and time reduction. Recently, an ICME study led by The Minerals, Metals, and Materials Society (TMS) [4] was conducted to identify, priority, and make detailed recommendations for the frameworks and key steps needed to implement ICME. The frameworks included a processing tool, a microstructure tool, and a property tool. Developing these tools for manufacturing process simulation remains significant challenges [5] .
This paper introduces ICME implementation framework for developing a product involving welding process for thin welded structures such as car bodies of automotive vehicles and high speed trains. An ICME approach to optimize welded structure design was outlined. The detailed heat source models, microstructure model, thermo- mechanical model, and property model used in welding simulation were discussed. The weld representations in a shell model for fusion welds and spot welds are introduced. A database creation method which is a key component in the ICME approach was discussed using modeling examples. This ICME approach allows considering the weld effects including material properties, joint strength, and residual stress during optimizing thin welded structures, which could greatly improve the safety of automotive vehicles and high-speed trains.
2. Optimizing Welded Structure Design
2.1. ICME Framework
An ICME implementation framework (Figure 1) for developing a product involving manufacturing processes such as welding was developed by generalizing the framework for automotive, aerospace, and maritime in [4] . This framework has been successfully used in designing automotive spot-weld structures [6] [7] , repairing aero- engine blades [8] , and designing composite-to-steel adhesive joined ship structures [9] .
As shown in Figure 1, the framework includes three major blocks: product requirements, manufacturing processes modeling tools, and final product. The product requirements include property requirement, design, and materials. The manufacturing process modeling tools include modeling inputs (process parameters), process tool (a thermal model, a microstructure model, and a property model), and performing prediction tools. The final product includes product validation and verification and final product configuring (material and design). There are 12 steps in the framework in which steps 8 and 11 are decision-making step.
2.2. Optimization Process Flow
The framework shows in Figure 1 is an ideal case. It is not practical and time consuming for each weld to go
![]()
Figure 1. ICME implementation framework.
through the calculation since a welded structure could include hundreds and thousands welds. Thus, a database approach was proposed to model each weld joint before a structure design as shown in Figure 2.
Figure 2 shows the optimization process flow to include weld effect in load, crash, and fatigue modeling. For a given prototype design such as a high speed train car body, weld joints are identified first and then the database will be checked for each weld to find the joint parameters (material properties, static strength, impact strength, and failure parameters). The joint parameters will be input to the model for the prototype design to conduct load, crash, and fatigue analyses. If analysis results show the design achieves the requirements, the optimization process is complete. A prototype based on the optimized design will be fabricated and tested, as shown in the step 10 of Figure 1. Otherwise, a new analysis will be conducted by changing welding parameters, plate thickness, and materials.
The database is the key component in the optimization process. Currently, welding processes in the database include fusion welding such as gas metal arc welding (GMAW) and resistance spot welding (RSW). Other welding processes such as laser welding and hybrid laser arc welding (HLAW) can be added to the database. The RSW database for mild steels and high strength steels with 0.5 mm to 2 mm thickness has been built for automotive applications. A database for aluminum alloys welded with laser welding and HLAW can be built for high-speed train design application. The database is strain-rate dependent and should cover at least three strain rates: low, middle and high since crash analyses for an automotive vehicle and high-speed train are conducted in high speed. Each weld will have a different speed during crash. A corresponding data for each weld can be obtained by interpolating the data in the database.
3. Models in the Process Tool
The process tool shown in Figure 1 includes a thermal-mechanical model, a microstructure model, and a property model. This section discusses the mathematical equation and physics in each model.
3.1. Welding Heat Source Models
Welding heat source models are a part of the thermal-mechanical model. Welding heat source models have been developed to predict temperature history during welding and cooling by inputting welding parameters. Based on the type of welding process, a corresponding model was developed to simulate the physics involved in the process. As an example, an incremental coupled thermal-electrical-mechanical model was developed for resistance spot welding (RSW) to predict the nugget size and temperature history [6] .
For fusion welding such as gas metal arc welding (GMAW), a moving-arc solution was developed using
![]()
Figure 2. ICME application in optimizing welded structure design.
Goldak double ellipsoidal heat source model which could be expressed as follows [10] :
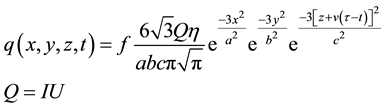 (1)
(1)
where f is a factor, h is arc Efficiency (0.85), I is welding current (255 A), U is welding voltage (25 V), and n is welding torch travel speed (4.969 mm/sec). a, b, c are the semi-axes of the ellipsoid.
Figure 3 shows a weld-cross macrograph, a Tee-joint mesh, and a predicted maximum temperature distribution using Goldak heat source model [10] . The material is DH36 and welding process is GMAW. The grey color shows the predicted fusion zone which is close to the weld fusion zone in the macrograph.
3.2. Microstructural Model
Many microstructure models were developed to predict microstructure and hardness near a weld such as Ashby microstructure model [11] , Bhadeshia thermodynamic and kinetic model [12] , and Gould analytical-based thermal and microstructure model [13] .
Microstructural models are used to predict the volume fraction of each microstructure phases and then calculate the hardness based on the predicted microstructure. Figure 4 shows an example of predicted hardness distribution in the weld and heat-affected zone (HAZ) for a four-pass pipe girth weld. The pipe material is a low alloy high strength steel and the filler material is ER120. The prediction was conducted using a standalone microstructure code [14] which was developed based on Ashby microstructure model. Because of fast cooling in the heat-affected zone (HAZ), martensite phase was formed in HAZ which results in higher hardness than inside the weld.
3.3. Thermal-Mechanical Model
Thermal-mechanical model was developed to predict thermal induced stress and deformation evolution during welding. Figure 5 shows a frame work of the thermal-mechanical model which couples with the thermal model and the microstructure model. The thermal model predicted temperature history as a function of location and time is input to the thermal-mechanical model. The microstructure change induced plasticity including volume change and phase transformation is considered in the thermal-mechanical model. Temperature dependent mechanical properties are input to the model. Strain-hardening, large deformation and melting/re-melting mechanisms are modeled for welding simulation.
![]()
Figure 3. Predicted temperature distributions for welding a tee joint using thermal model.
![]()
Figure 4. Predicted Vickers Hardness distributions for a multi-pass weld.
![]()
Figure 5. Frame work of thermal-mechanical model.
3.4. Property Model
A property model was developed to predict weld material properties, static strength, impact strength, and failure parameters of a weld joint. The joint property and failure parameters will be input to Step 9 as shown in Figure 1 to predict the product performance by applying loads.
Weld static tensile strength can be estimated from the predicted hardness using the microstructure model. For example, static tensile strength of steels (sstatic, MPa) can be calculated from the following equation.
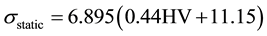 (2)
(2)
The equation was developed by fitting the curve in [15] in which HV is the Vickers hardness with 10 kgf.
The impact strength depends on the impact speed. Experimental testing at a series of strain rate can be conducted for a material to establish the relationship between material tensile strength and strain rate. Based on the relationship, the impact strength can be estimated for an impact speed.
Wilkins cumulative strain damage model [16] , as shown in Equation (3), has been used to predict the failure in the weld joint for fusion welding [17] .
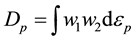 (3)
(3)
where ep is the equivalent plastic strain, w1 is the hydrostatic-pressure weighting term, and w2 is the asymmetric- strain weighting term. When the cumulative damage strain Dp exceeds a critical value Dc, discontinuous macro- crack will occur and grove step-wisely. The critical value Dc can be determined by experimental testing and modeling [17] .
Daimler Chrysler failure model, as shown in Equation (4), has been used to predict resistance spot weld failure [7] . It is a stress-based failure model considering tension stress, bending stress, and shearing stress.
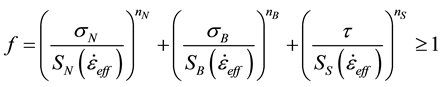 (4)
(4)
where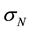 ,
, 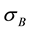 , and
, and 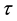 are axial (normal) stress, bending stress, and shear stress, respectively.
are axial (normal) stress, bending stress, and shear stress, respectively. 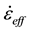 is effec- tive strain rate and
is effec- tive strain rate and ,
, 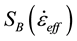 , and
, and 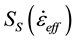 are strain-rate dependent axial strength, bending strength, and shear strength at failure. The model includes six failure parameters (SN, SB, SS, nN, nB, and nS) which can be determined by testing and modeling [7] .
are strain-rate dependent axial strength, bending strength, and shear strength at failure. The model includes six failure parameters (SN, SB, SS, nN, nB, and nS) which can be determined by testing and modeling [7] .
4. Representing Welds Using Shell Elements
4.1. Fusion Weld Representation
Shell models are typically used by thin welded structure because of thin material thickness. Weld detailed geometry cannot be included in a shell model. To allow industries to include a weld joint in their structure design, methods to represent a weld joint using shell elements were developed [18] [19] . Analysis results showed that the shell-element model can predict the similar mechanical behavior as a detailed solid-element model [18] .
Figure 6 shows an example how to model a butt joint using shell elements. The middle surface, a dot line in the weld cross section, was used as reference surface to create the shell element mesh. The weld bead area, showing with red color, is thicker than other area. Fine meshes are used near a weld and coarse meshes are used in the area far away from a weld. Similar welding distortion was predicted by a shell model and a solid model although the weld bead shape is greatly simplified in the shell model.
Figure 7 shows how to represent a lap joint using shell elements. The yellow dot line on the weld cross section macrograph was used as a reference surface to create the shell elements. Five integration points were used in a weld simulation to model the temperature gradient in the thickness direction.
Figure 8 shows two methods to represent a Tee joint using shell elements. Both methods were evaluated to predict weld induced distortion. For a thick structure, both methods works well if the thickness is defined correctly in the weld shell elements. For a thin automotive structure, Method 1 is working better than Me-
![]()
Figure 6. Butt joint shell element modeling method [18] .
![]()
Figure 7. How to represent a lap joint with shell elements.
![]()
Figure 8. How to represent a Tee joint with shell elements (a) Method 1 (b) Method 2.
thod 2. However, to simplify the mesh generation in a large automotive structure, Method 2 could also be selected, as shown in Figure 9. Figure 9 also includes examples on how to represent a butt joint, and a lap joint using shell elements in a thin-welded structure.
4.2. Spot Weld Representation
Spot welds were used to model by rigid links or beam elements in early days. Spot weld mechanical performance cannot be accurately predicted. With high strength steels increasingly used in automotive structures, the failure prediction of spot welds becomes critical to predict the mechanical performance correctly. Solid-element approach was developed and implemented in commercial software LS-Dyna [20] . A spot weld can be repre- sented by one solid element, as shown in Figure 10(a), for KSII, coach peel, and lap shear sample. A spot weld can also be represented by 4, 8, and 16 solid elements [21] . The component in Figure 10(b) includes about 40 spot welds in the structure. Each spot weld was represented by 8 solid elements.
5. Building Database
5.1. Spot-Weld Database
Spot-weld database includes weld properties and failure parameters for Equation (4). To create the database, testing and modeling were conducted in three strain rates: low, middle, and high. Figure 11 shows a spot weld- ing setup, process parameters (force and current), weld macrograph, and process modeling method and results. Spot weld process was modeled by a coupled thermal-electrical-metallurgical-mechanical model. The predicted nugget size is close to the weld macrograph. By inputting the predicted temperature history to the microstructure model, the spot hardness distribution was predicted which was very close to the measured one.
With the predicted hardness, the tensile strength of spot weld was estimated using Equation (2). Then the yield strength of spot weld can be estimated from the tensile strength. By assuming the spot weld has the same elastic and tangential modulus as the base material, a bi-linear stress strain curve can be established and save in the spot weld database.
Spot-weld failure parameters were developed by conducting six tests: KSII loading in 0, 30, 60, and 90 degree,
![]()
Figure 9. Applying shell modeling method in a thin welded structure.
![]() (a) (b)
(a) (b)
Figure 10. Spot-weld representation in a component (a) Sample modeling; (b) Component modeling.
coach peel, and lap shear [7] . The six tests were modeled with the same mesh size (see Figure 10) as a global automotive structure since stress depends on the mesh size. The model predicts a peak stress (strength) in tension, bending, and shear. By solving set sets of equations, the six failure parameters in Equation (4) can be obtained.
Figure 12 shows the testing and modeling of KSII sample with 90-degree loading. The model predicts the deformation evolution during load and the failure of spot welds. Figure 13 shows the testing and modeling of lap shear sample. The testing fixtures were included in the model. The material is 50 ksi steel with 1 mm thickness for one sheet and 2 mm thickness for another sheet. Two analyses were conducted to check the effect of spot weld material properties. By inputting the base material properties for the spot weld, the analysis under predict the load. By inputting the predicted spot weld material properties from the process model, the predicted load can match with the experimental measurement.
The testing and modeling developed material properties and failure parameters in samples were verified in a component level before applying to a large thin welded structure. Figure 14 shows a designed T-component made with about 40 spot welds. The finite element mesh of the component is shown in Figure 12. Analysis results show that the spot welds fail during loading. It should be pointed out that spot-weld failure modes cannot
![]()
Figure 12. Failure prediction of KSII-90 sample.
![]() (a) (b) (c)
(a) (b) (c)
Figure 13. Lap-shear sample modeling (a) Testing set up; (b) Sample mesh; (c) Load-time curves.
predict because of coarse mesh which requires find mesh in the spot weld as discussed in [6] . Once cracks ini- tiate, the model thinks the spot weld fail completely. Currently, the damage parameters are developed to refine the model.
5.2. Fusion-Weld Database
Fusion-weld database as a function of strain rate can be built. Welding process models for a butt joint, a lap joint, and a Tee joint have been developed to predict hardness and weld residual stress. Mechanical models have been developed to obtain the failure parameter for Equation (3).
As an example, Figure 15 shows predicted temperature and stress distributions and comparisons of temperature and displacement between testing and modeling for a lap-joint. The lap joint joins two 125 mm wide and 300 mm long plates with a 150 mm long weld in the middle. High tension stresses were predicted on the area away from the weld toe because of weld shrinkage induced bending deformation. Six models were analyzed to identify the best one close to experiment. It was found that the model shown in Figure 7 produces the best result
![]()
Figure 14. Database verification test and modeling on a component.
which can be used to build the fusion-weld database. Similar excises were conducted for butt joint and lap joint to identify the best model.
6. Load, Crash, and Fatigue Analysis
Once the database is built for spot welds and fusion welds, weld effects such as material property change, joint strength, and residual stress can be modeled in the load, crash, and fatigue analysis of thin welded structures such as automotive vehicles and high-speed train car bodies. The long-term goal is to connect the database to the commonly used commercial software such as LS-Dyna to automate the simulation process. This ICME approach will improve the current structure design in industries to result in a better product and reduce the weld failures during service.
7. Summary
Weld effects on material property change, joint strength, and residual stress are ignored in industries during designing welded structures because of lack of methods and data. ICME has been gradually accepted by industries to speed up product development and produce new materials. To help apply ICME in designing weld structures, an ICME approach was proposed and implemented by building a weld database through modeling and testing. The ICME approach mainly focus on thin structures such as automotive vehicles and high-speed train car bodies. This approach can be used to optimize structure design for better and safe product.
The weld database as a function of strain rate can be built by testing and modeling. The weld modeling uses heat source models for heat transfer analysis, a microstructural model for microstructure and hardness prediction, a thermo-mechanical model to predict residual stress and deformation, and a property model to estimate the weld joint strength.
Since thin structures are often modeled using shell elements, detailed weld geometry cannot be represented using shell elements. Fusion weld and spot weld representation methods with shell elements were developed to allow designers to include weld effects during load, crash, and fatigue analysis.
Spot-weld database as a function of strain rate has been established by modeling and testing which include material properties and failure parameters for a spot weld as a function of materials, thickness, and weld size. Fusion weld database as a function of strain rate can also be built by testing and modeling.
Acknowledgements
The authors want to thanks the Project, called “Influence on the corrosion behavior of residual stress and control technology of aluminum alloys trains carbodies (2682014CX003)” of the scientific and technological innovation projects of Chinese universities.
NOTES
*Corresponding author.