Influence of Control Modes of Grid-Connected Solar Photovoltaic Generation on Grid Power Flow ()
1. Introduction
For nearly a century, most countries have relied on just one model of power distribution: sending electricity over huge transmission grids from big central generating plants to customers in their homes, offices and factories [1] . A parallel trend, however, has been developing in recent years, in which significantly smaller sized generation units are being connected at the distribution level. This technology is called Distributed Generation (DG). The portfolio of DG technologies includes reciprocating engines, micro turbines, combustion gas turbines (including mini turbines), solar thermal, fuel cells, wind turbines and Solar Photovoltaics (PV). Recent studies suggest that in medium and long terms, PV generator will become commercially so attractive that large-scale implementation of this type can be seen in many parts of the world [2] [3] .
Due to the significant advantages of grid-connected PV systems, this paper focuses on this type of DG tech- nology. Grid-connected PV systems
・ will reduce the power bill as it is possible to sell surplus electricity produced to the local electricity supplier, comparatively easier to install as they do not require a battery system.
・ are comparatively easier to install as they do not require a battery system.
・ have the advantage of effective utilization of generated power because there are no storage losses involved.
・ are growing rapidly due to accelerated cost reductions and associated growth in production. As these tech- nologies mature they have the potential to provide an increasing share of electricity demand.
However, integration of Solar Photovoltaic (PV) generation into an existing distribution system has many im- pacts on the system, with the power flow being one of the major issues. This impact is not generic for any net- work, but it may manifest itself either positively or negatively, depending on the grid configuration, interface control modes, operation mode, and load profile [4] . Grid-connected PV systems have three control options of the local voltage controller of the interface DC-AC converter. These control modes are Power Factor (PF) con- trol, Voltage (V) control, and Droop Voltage (DV) control.
The paper quantifies the influence of the three control options on the bus voltages and power losses of the host distribution network. For achieving this objective the power flow approach has been used, which is consi- dered as the optimal tool for analyzing the steady state operation of the network.
2. Power Flow in Active Distribution Networks
2.1. Overview
Modern distribution systems were designed to accept bulk power at the bulk supply transformers and to distri- bute it to customers. Thus the flow of both real power 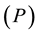 and reactive power
and reactive power  was always from the higher to the lower voltage levels. However, with PV generators, the distribution network is no longer a passive circuit supplying loads but an active system with power flows and voltages determined by the generation as well as the loads. The voltage source convertor of the PV generator will allow export of real and reactive power but may introduce harmonic currents. Thus the power flows through the circuits may be in either direction depend- ing on the relative magnitudes of the real and reactive network loads compared to the generator outputs and any losses in the network. The change in real and reactive power flows caused by PV generators has important tech- nical and economic implications for the power system. However, additional operational costs can be avoided through optimal correction in electrical systems [5] .
was always from the higher to the lower voltage levels. However, with PV generators, the distribution network is no longer a passive circuit supplying loads but an active system with power flows and voltages determined by the generation as well as the loads. The voltage source convertor of the PV generator will allow export of real and reactive power but may introduce harmonic currents. Thus the power flows through the circuits may be in either direction depend- ing on the relative magnitudes of the real and reactive network loads compared to the generator outputs and any losses in the network. The change in real and reactive power flows caused by PV generators has important tech- nical and economic implications for the power system. However, additional operational costs can be avoided through optimal correction in electrical systems [5] .
The power flow approach in distribution networks hosting PV generators differs from the conventional one mainly in two issues; the selection process of the slack bus and the modelling of the generation buses. In a transmission network, a bus with a large generating unit is usually chosen as the slack bus. In a distribution network, the bus where the distribution system under investigation is connected to a higher voltage level is usually chosen as the slack bus. The complex voltage is specified at slack bus; the voltage angle is usually set to zero [6] .
2.2. Operation Modes of a PV Generator
The PV generator bus is modelled through one of three models depending on the control mode of the converter. Three control modes are considered [7] [8] :
- Power Factor (PF) Control
The PF control of the converter is enabled, i.e. the converter operates at constant power factor. The used bus model is PQ type, i.e. the injected 
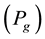 and injected
and injected 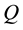
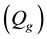 are specified.
are specified.
 (1)
(1)
where 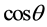 is the set PF.
is the set PF.
This operation mode has two constraints: the rated MVA of the converter may not be violated, and the PF should be maintained constant.
- Voltage Control
The voltage control of the converter is enabled; that means, the converter operates at variable power factor operation. The used bus model is PV type, i.e. the injected  and the voltage magnitude are specified. This operation mode allows the generator to support the voltage profile in the network through injecting reactive power. Voltage control can be done locally, i.e. the reactive power output of the generator is controlled to achieve the specified local voltage at its terminal. The active power output is constant for the dispatch.
and the voltage magnitude are specified. This operation mode allows the generator to support the voltage profile in the network through injecting reactive power. Voltage control can be done locally, i.e. the reactive power output of the generator is controlled to achieve the specified local voltage at its terminal. The active power output is constant for the dispatch.
- Droop Voltage Control
For this control mode the voltage is controlled according to a specified droop (e.g. droop = 2%) and set vol- tage. The droop is defined as:
 (2)
(2)
The generation bus model for this mode is DV type, which is new for power flow calculations (i.e. not in- cluded in the conventional power flow). The generator can be set to control the local voltage at its terminal to a specified set point. With droop control the set point is not reached in any case because the set point is moved (by DV droop) as more reactive power is needed to reach the original voltage set point of the PV generator. The ad- vantage of the droop control is that more than one machine at one bus could control the voltage as well as the participation of the single machine could be configured with the setting of the droop value. When set to voltage control, a droop value can be entered. The voltage at the local bus is then controlled according to the following equations [7] :
 (3a)
(3a)
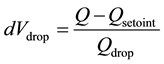 (3b)
(3b)
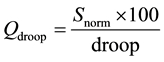 (3c)
(3c)
where
 is the actual voltage value at the terminal busbar.
is the actual voltage value at the terminal busbar.
 is the specified voltage set point of the PV generator.
is the specified voltage set point of the PV generator.
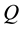 is the actual reactive power output of the PV generator.
is the actual reactive power output of the PV generator.
![]() is the specified dispatch reactive power of the PV generator.
is the specified dispatch reactive power of the PV generator.
![]() is the nominal apparent power.
is the nominal apparent power.
![]() is the droop value specified in percentage.
is the droop value specified in percentage.
3. Evaluation Criteria (Indices)
For achieving a systematic methodology to quantify the required impact, a set of evaluation criteria and indices are defined and mathematically formulated.
3.1. Penetration Index (Penetration Level)
The penetration level of distributed generation (DG) on the distribution network is measured against total load demand or the percentage of DG power referred to the rated power of the network [8] -[11] . It is defined as the ratio of the PV capacity to the peak load of the hosting distribution network
![]() (4)
(4)
3.2. Dispersion Index (Dispersion Level) [8]
It is defined as the ratio of the number of PV buses to the number of load buses:
![]() (5)
(5)
This index points out to the geographic dispersion of PV generators and not its capacity.
3.3. Voltage Rise Index [6]
Voltage rise index (VRI%) for a bus is the ratio of the difference between bus voltage with PV generation and bus voltage without PV generation, to the bus voltage without PV generation:
![]() (6)
(6)
The German VDEW code allows VRI% = 2% as a maximum. This figure is suitable for strong grids. But for weak grids, this index is useful only as an indicator for the voltage support degree by PV. Therefore I suggest an alternative index VRI2%, which indicates the voltage rise relative to the nominal voltage:
![]() (7)
(7)
3.4. Total Loss Index [6]
It is defined as the ratio of the power loss (![]() or
or![]() ) in the active host grid to the power loss in the passive host grid:
) in the active host grid to the power loss in the passive host grid:
![]() (8)
(8)
This index shows the reduction or increase of total losses caused by PV inclusion relative to the original losses, but it gives no information about the loss rate relative to the input power (![]() or
or![]() ). Therefore further power loss indices are introduced, referred to as ΔPI% and ΔQI%, and defined as:
). Therefore further power loss indices are introduced, referred to as ΔPI% and ΔQI%, and defined as:
![]() (9a)
(9a)
![]() (9b)
(9b)
4. Test Network
Several simulations have been carried out using a typical distribution grid with the voltage level 20/0.4 kV. The test network is shown in Figure 1 with several PV units, which can be connected or disconnected to the grid through corresponding circuit breakers. The load profile has been determined so that the passive grid (base case) represents a weak network, Viz. a network with a bad voltage profile. The test network consists of 12 buses, 9 lines, 9 distributed line loads and 4 concentrated loads at the critical buses 2, 8, 9, and 12.
5. The Algorithm
Based on the mathematical models and the requirements of the used program Dig Silent Power Factory (Dig Si- lent-PF) V14.1.3, which is a computer aided engineering tool for the analysis of electrical power systems, an algorithm has been developed. The algorithm is designed so that it can be applied to any active distribution grid with multiple voltage levels and different PV configurations. This algorithm will be adopted to investigate the test network. The developed approach is shown as a flow chart in Figure 2.
6. Computer Simulations
6.1. Based Case
Initially a power flow was carried out for the distribution network without PVs (Base Case). The results show that the network has two problems: Significant total ![]() and
and ![]() losses, whose ratios are 6.45% and 8.3% re- spectively, and under voltage of the half of buses (Figure 3).
losses, whose ratios are 6.45% and 8.3% re- spectively, and under voltage of the half of buses (Figure 3).
![]()
Figure 3. Bus voltage of the network for base case.
To evaluate the impact of PV on power flow of base case, several scenarios was simulated. These scenarios include connecting PV units to the grid with different capacities (i.e. different PL%) and locations (i.e. different DI%).
6.2. Connecting a 200 KVA-PV at Bus 8
The connection of a single PV generator at bus 8 with the three control modes has, in general, improved the network performance, but to an extent that is depending on the control mode. The major impacts are:
- The voltage profile at all buses has been improved and became acceptable (Figure 4).
- The power flows are reversed on several lines.
- Figure 5 shows voltage rise index (VRI%) of network buses for the three control modes. It is clear that the PF control gives the highest VRI with an average value of 10.2% for the buses 5, 6, and 7, which are adjacent to the PV connection bus 8. The Droop voltage control gives the next best average value of VRI (8.2%), while the voltage control gives the lowest VRI (7.7%).
- The ![]() losses index
losses index ![]() has been reduced to 3.23% for the PF control and the droop voltage control and unchanged for
has been reduced to 3.23% for the PF control and the droop voltage control and unchanged for ![]() control, while
control, while ![]() losses index
losses index ![]() increased for
increased for ![]() control to 10.5% while remained unchanged as for the base case for DV and PF control modes (Figure 6).
control to 10.5% while remained unchanged as for the base case for DV and PF control modes (Figure 6).
6.3. Connecting 300 kVA PV at Bus 8
A PV generator of a much more capacity (300 kVA) is connected to the same bus 8. The simulation results show the following impacts:
Ø The impact on bus voltages are shown in Figure 7. The voltage profile has been well improved. Again, the PF control gives the highest voltages. But due to the higher penetration level of this scenario, the voltages of at least 3 buses, namely the PV connection bus 8 (1.1 pu), and the close adjacent buses 5, 6 and 7, violate the upper limit (1.05 pu). Even, the voltage of bus 8 violates the 1.05 limit for Droop control. Therefore, it is recommended to determine the maximum PV capacity allowed to be added to the bus. In this case study, the maximum allowed PV capacity was found to be 230 kVA.
Ø Concerning the ![]() and
and ![]() losses indices (
losses indices (![]() and
and![]() ), adding the 300 kVA PV causes the follow- ing impacts relative to the base case of the network (Figure 8):
), adding the 300 kVA PV causes the follow- ing impacts relative to the base case of the network (Figure 8):
- For PF control, ![]() is unchanged, while
is unchanged, while ![]() increases by about 30% relative to base case.
increases by about 30% relative to base case.
- For both ![]() and DV control,
and DV control, ![]() becomes about 3 times and 2 times respectively relative to that of base case, while
becomes about 3 times and 2 times respectively relative to that of base case, while ![]() becomes 5 times and 3 times respectively.
becomes 5 times and 3 times respectively.
These negative impacts on voltages and power losses occurred mainly because of the high penetration level (about 100%); so it is recommended to avoid that as it is explained in the next section.
6.4. Impact of Penetration Level on Power Flow
With the interconnection location being fixed (i.e. DI% is fixed), the impacts of PV with PF control mode on power flow with different capacities are investigated. Figure 9 shows the impact of different PL on the power
![]()
Figure 4. Bus voltage for control modes of a 200 kVA PV generation at bus 8.
![]()
Figure 5. Voltage rise index of buses caused by 200 kVA PV at bus 8.
![]()
Figure 6. Power loss indices (∆PI% and ∆QI%) for 200 kVA PV at bus 8.
loss in the host grid. From the trend lines plotted on the basis of simulation results for PF control mode, it is ob- vious that for low PV penetration levels ![]() and
and ![]() losses decrease reaching a minimum for almost PI = 30% and 70% respectively, while losses increase for higher penetration levels and particularly
losses decrease reaching a minimum for almost PI = 30% and 70% respectively, while losses increase for higher penetration levels and particularly ![]() losses reach val- ues that are much higher than losses of base case from PI of 55% onwards.
losses reach val- ues that are much higher than losses of base case from PI of 55% onwards.
![]()
Figure 7. Bus voltages for 3 control modes of 300 kVA PV at bus 8.
![]()
Figure 8. Power loss indices for 3 control modes of 300 kVA PV at bus 8.
![]()
Figure 9. Power loss indices as a function of penetration level for PF control.
7. Conclusions
The simulation results show that the connection of a single PV generator at a bus with the three control modes has, in general, improved the network performance, but to an extent that is depending on the control mode and penetration level (PL%). The power factor (PF) control gives the highest voltage rise index (VRI) for buses which are adjacent to the PV connection bus. The Droop voltage control gives the next best average value of VRI, while the voltage control gives the lowest VRI. With a higher penetration level (about 60% - 70% PL), the PF control causes that the voltages of the PV connection bus and its adjacent buses violate the upper voltage limit.
For PF control mode with low PV penetration levels, ![]() and
and ![]() losses decrease reaching a minimum for almost PL of 30% and 70% respectively, while losses increase for higher penetration levels, and particularly
losses decrease reaching a minimum for almost PL of 30% and 70% respectively, while losses increase for higher penetration levels, and particularly ![]() losses reach values that are much higher than losses of base case from PL of 55% onwards.
losses reach values that are much higher than losses of base case from PL of 55% onwards.
It is recommended to determine the maximum PV capacity allowed to be added to the desired bus for the concerned network, in order to avoid the negative impacts on the network performance.