A Computational Quadruple Laplace Transform for the Solution of Partial Differential Equations ()
1. Introduction
Many engineering and science fields encounter linear or non-linear partial differential equations describing the physical phenomena. A number of methods (for example, approximate and exact methods) can be used to determine the solutions of differential equations. Mostly, it may be complicated to solve these equations analytically. Such equations are commonly solved by integral transforms such as Laplace and Fourier transforms and the worth of Laplace and Fourier transforms lies in their ability to transform differential equations into algebraic equations, which allows a systematic and simple way to find solution. The numerical methods can provide approximate solutions rather than analytic solutions of the problems [1] . A number of aspects of these methods have been studied in [2] [3] .
The Laplace transform has been effectively used to solve linear and non-linear ordinary and partial differential equations and is used extensively in electrical engineering. The Laplace transform reduces a linear differential equation to an algebraic equation, which can be solved by rules of algebra. The original differential equation can then be solved by applying the inverse Laplace transform. The Heaviside first proposed a scheme, without using the Laplace transform (see [4] and references therein).
Eltayeb and Kiliçman [5] applied double Laplace transform to find the solution of general linear telegraph and partial integro-differential equations. Dahiya and Najafai [6] established new theorems for calculating the Laplace transforms of n-dimensions and application of these theorems to a number of commonly used special functions was considered, and in the end, authors solved one-dimensional wave equation involving special functions using two dimensional Laplace transforms. Aghili and Moghaddam [7] presented a new theorem and corollary on multi-dimensional Laplace transformations. Authors further developed some applications based on these results. Kiliçman and Eltayeb [8] discussed the relationship between Sumudu and Laplace transforms and further made some comparison on the solutions. Authors provided some counter examples. Cheniguel and Reghioua [9] investigated the solution of three-dimensional diffusion equation with non-local condition using Adomian decomposition method. Atangana [4] introduced the triple Laplace transform. Author discussed some properties and theorems about the triple Laplace transform. Moreover, author used the operator to solve some kind of third-order differential equation.
The aim of this paper is to discuss some properties and theorems about the quadruple Laplace transform and give a good strategy for solving the fourth order partial differential equations in engineering and physics fields, by quadruple Laplace transform.
First of all, we recall the following definitions.
The double Laplace transform of a continuous function  can be defined [5] [10] as
can be defined [5] [10] as
 (1.1)
(1.1)
where x, y > 0 and p, q are Laplace variables.
The inverse double Laplace transform is defined as
 (1.2)
(1.2)
The triple Laplace transform [4] of a continuous function  can be defined as
can be defined as
 (1.3)
(1.3)
where x, y, z > 0 and p, q, r are Laplace variables.
The inverse triple Laplace transform is defined as
 (1.4)
(1.4)
In the following section definitions of quadruple Laplace transform, its inverse and some of its properties are presented.
2. Definitions and Properties
Before launching into the main part of the paper, we define some notations and terminologies which will remain standard.

Quadruple Laplace transform: Let f be a continuous function of four variables, then, the quadruple Laplace transform of  is defined by
is defined by
 (2.1)
(2.1)
where w, x, y, z > 0 and p, q, r, s are Laplace variables.
It is to be noted that the quadruple Laplace transform operator is linear.
 (2.2)
(2.2)
Now, if the quadruple Laplace transform is known, its inverse is given by
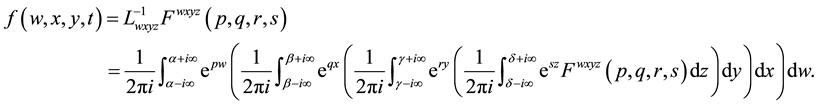 (2.3)
(2.3)
Quadruple Laplace transform for some partial derivatives of function of four variables are given as
1) Quadruple Laplace transform for first order partial derivative of function of four variables
 (2.4)
(2.4)
2) Quadruple Laplace transform for second order partial derivative of function of four variables
 (2.5)
(2.5)
 (2.6)
(2.6)
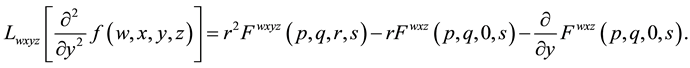 (2.7)
(2.7)
3) Quadruple Laplace transform for the mixed fourth order partial derivative of function of four variables
 (2.8)
(2.8)
![]() (2.9)
(2.9)
The uniqueness and existence of the quadruple Laplace transform is discussed in the following section.
3. Uniqueness and Existence of the Quadruple Laplace Transform
Consider ![]() be a continuous function on the interval
be a continuous function on the interval![]() . Also, assume that
. Also, assume that ![]() is of exponential order, that is, there exists some constants
is of exponential order, that is, there exists some constants ![]() such that
such that ![]() satisfy the fol- lowing condition
satisfy the fol- lowing condition
![]() (3.1)
(3.1)
The quadruple Laplace transform
![]() (3.2)
(3.2)
exists for all![]() ,
, ![]() ,
, ![]() ,
, ![]() and satisfy the condition (3.1). The following theorem explains the uniqueness.
and satisfy the condition (3.1). The following theorem explains the uniqueness.
Theorem 1. Let ![]() and
and ![]() is defined be continuous functions defined for w, x, y, z ≥ 0 and having Laplace transforms,
is defined be continuous functions defined for w, x, y, z ≥ 0 and having Laplace transforms, ![]() and
and ![]() respectively. If
respectively. If ![]() , then
, then![]() .
.
Proof If ![]() are sufficiently large. Then, from the definition of the quadruple inverse Laplace transform, we have
are sufficiently large. Then, from the definition of the quadruple inverse Laplace transform, we have
![]() (3.3)
(3.3)
Using the hypothesis, ![]() , the expression (3.3) can be written as
, the expression (3.3) can be written as
![]() (3.4)
(3.4)
this completes the proof.
4. Convolution Theorem for the Quadruple Laplace Transform
In this section, we will give some definitions of convolution for functions and state the convolution theorem of the quadruple Laplace transform.
Consider the functions![]() ,
, ![]() ,
, ![]() and
and![]() .
.
The convolution of functions ![]() and
and ![]() can be defined as
can be defined as
![]() (4.1)
(4.1)
The convolution of functions![]() ,
, ![]() and
and ![]() can be defined as
can be defined as
![]() (4.2)
(4.2)
Similarly, the convolution of functions![]() ,
, ![]() ,
, ![]() and
and ![]() can be defined as
can be defined as
![]()
Theorem 2. (Convolution Theorem) If
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
are convergent at the point ![]() and if
and if
![]() (4.6)
(4.6)
is absolutely convergent, then, the following expression
![]() (4.7)
(4.7)
is the Laplace transform of the function
![]() (4.8)
(4.8)
and the integral
![]() (4.9)
(4.9)
is convergent at the point![]() , see the proof in [11] .
, see the proof in [11] .
5. Properties of Quadruple Laplace Transform
In this sectioon, some properties of quadruple Laplace transform are presented
Property (1)
![]() (5.1)
(5.1)
Proof: By definition (2.1) of quadruple Laplace transform left hand side of (5.1) can be solved as
![]() (5.2)
(5.2)
The inner integral with respect to z in Equation (5.2) can be solved after proper substitution as
![]() (5.3)
(5.3)
Equation (5.2) becomes
![]() (5.4)
(5.4)
The inner integral with respect to y in Equation (5.4) can be solved after proper substitution as
![]() (5.5)
(5.5)
After substituting the value from Equation (5.5) in Equation (5.4), we can get
![]() (5.6)
(5.6)
On the similar lines, integrating Equation (5.6) twice accordingly, we can obtain required result Equation (5.1).
Property (2)
![]() (5.7)
(5.7)
Proof: By definition (2.1) of quadruple Laplace transform right hand side of (5.7) can be solved as
![]() (5.8)
(5.8)
The inner integral with respect to z can be solved, after proper substitution as
![]() (5.9)
(5.9)
On the similar lines, integrating Equation (5.9) with respect to y, x, w after proper substitution, we can obtain required result Equation (5.7).
Property (3)
![]() (5.10)
(5.10)
Proof: By definition (2.1) of quadruple Laplace transform left hand side of (5.10) can be solved as
![]() (5.11)
(5.11)
The inner integral with respect to z can be solved by parts and gives
![]() (5.12)
(5.12)
Equation (5.11) becomes
![]()
On the similar lines, integrating Equation (5.13) accordingly with respect to y, x, w, we can obtain required result Equation (5.10).
Theorem 3. A function ![]() which is continuous on
which is continuous on ![]() and satisfies the growth condition (3.1) can be recovered from only
and satisfies the growth condition (3.1) can be recovered from only ![]() as
as
![]() (5.13)
(5.13)
To check the efficiency of the theorem, we consider the following example.
Let ![]() for which Laplace transform can easily be found as
for which Laplace transform can easily be found as
![]() (5.14)
(5.14)
Taking higher order mixed derivatives of Equation (5.14), leads
![]()
Using (5.14) and theorem 5.1, yields
![]()
Using the application of logarithm and the L’Hospital’s rule on the previous expression reveals
![]() (5.15)
(5.15)
6. Numerical Examples
To illustrate the applicability and effectiveness of our method, some examples are constructed in this section.
Example 4.1. Consider the following fourth order partial differential equation
![]()
Applying quadruple Laplace transform ![]() on both sides of Equation (6.1), gives
on both sides of Equation (6.1), gives
![]() (6.1)
(6.1)
where
![]() (6.2)
(6.2)
After substituting the value, Equation (6.1) becomes
![]() (6.3)
(6.3)
Applying the quadruple inverse Laplace transform on (6.3)
![]() (6.4)
(6.4)
Example 4.2. Consider the following three-dimensional diffusion equations [9]
![]()
Applying quadruple Laplace transform ![]() on both sides of Equation (6.5), gives
on both sides of Equation (6.5), gives
![]() (6.5)
(6.5)
where
![]() (6.6)
(6.6)
After substituting the value of![]() , Equation (6.5) becomes
, Equation (6.5) becomes
![]() (6.7)
(6.7)
Applying the quadruple inverse Laplace transform on (6.7)
![]() (6.8)
(6.8)
Example 4.3. Consider the following non-homogeneous fourth order partial differential equation
![]()
Applying quadruple Laplace transform ![]() on both sides of Equation (6.9), gives
on both sides of Equation (6.9), gives
![]() (6.9)
(6.9)
where
![]() (6.10)
(6.10)
After substituting the value of![]() , Equation (6.9) becomes
, Equation (6.9) becomes
![]() (6.11)
(6.11)
Applying the quadruple inverse transform on (11)
![]() (6.12)
(6.12)
Example 4.4. Consider the following non-homogeneous three-dimensional diffusion equation
![]()
Applying quadruple Laplace transform ![]() on both sides of Equation (6.13), gives
on both sides of Equation (6.13), gives
![]() (6.13)
(6.13)
where
![]() (6.14)
(6.14)
After substituting the value![]() , Equation (6.13) becomes
, Equation (6.13) becomes
![]() (6.15)
(6.15)
Applying the quadruple inverse transform on (6.15)
![]() (6.16)
(6.16)
7. Conclusion
In this paper, we extend the work of [4] [5] to quadruple Laplace transform. Existence and uniqueness of the quadruple transform are also discussed in this work. Some properties, theorems using the new quadruple Laplace transform and a table in which quadruple Laplace transform applied on some functions have also been presented. It is analyzed that our proposed method is well suited for use in partial differential equation involving four variables. Therefore, the present method is an accurate and reliable technique for the partial differential equations.
Appendix
![]()
Table 1. of quadruple Laplace transform Lwxyz for functions of four variables.