Micromagnetic Investigation of Microwave Permeability of Magnetic Artificial Spin Ice ()
1. Introduction
With the development of micro/nano-fabrication techniques, the exploration of nanometer-sized magnetic elements has markedly expanded in the recent years for their potential applications in advanced storage media, advanced microwave technologies, and novel spintronic devices. Recently, ferromagnetic frustration in “artificial spin ince” (ASI) was attracting intensive study [1] - [3] . ASIs are patterned nanoscale structures in which each element is small enough to have essentially uniform magnetization. The geometrical arrangement of the structures in the lattice leads to frustration by design to act as analogs of bulk geometrically frustrated materials [1] [4] . As these artificial structures are fabricated via nanolithography and thin film deposition, it is possible to engineer system parameters such as lattice geometry, inter-elemental dipolar coupling strength, moment switching behavior, and quenched disorder. In this work, we have calculated the microwave permeability of magnetic artificial spin ice consisting of stadium like elements on a square lattice using micromagnetic simulations. The complex permeability spectra of these artificial structures with different magnetic states are investigated. The permeability of ASIs at various magnetic field strength is also calculated, as well as their dependence on the spacing gap between the neighboring elements.
2. Method
The micromagnetic simulations are performed using a three-dimensional object-oriented micromagnetic framework (OOMMF) by solving the Landau-Lifshitz-Gilbert (LLG) equation as a function of time [5] . The microwave permeability spectra are obtained following the field-pulse processes [6] - [9] . The stable ground state of the magnetizations was firstly obtained by minimizing the total energy. Then, using the ground state as the initial state, the susceptibility is obtained by exciting the system with a small external field having a time dependence 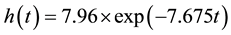 A/m (
A/m (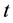 in ns), which is applied along the
in ns), which is applied along the 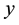 axis as shown in Figure 1(a). The Fourier transform of this expression leads to
axis as shown in Figure 1(a). The Fourier transform of this expression leads to 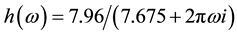 (
(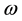 in GHz). This form has a significant response up to 20 GHz, which enables us to calculate the susceptibility up to this frequency. This field is spatially homogeneous and is introduced in the density functional of the Zeeman term. The amplitude of the driving field is very small to minimize nonlinear behaviour. We define the spatial average susceptibility in the direction
in GHz). This form has a significant response up to 20 GHz, which enables us to calculate the susceptibility up to this frequency. This field is spatially homogeneous and is introduced in the density functional of the Zeeman term. The amplitude of the driving field is very small to minimize nonlinear behaviour. We define the spatial average susceptibility in the direction 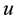 as
as
 (1)
(1)
where
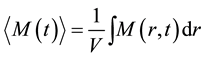 (2)
(2)
Performing FFTs on the excitation and the response, the obtained expression of the susceptibility can be directly calculated:
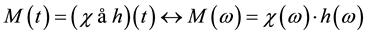 (3)
(3)
Based on the calculated dynamic susceptibility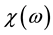 , the microwave permeability
, the microwave permeability 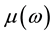 can be derivate as
can be derivate as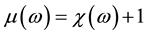 .The material parameters in OOMMF for Permalloy (Py) are taken: saturation magnetization
.The material parameters in OOMMF for Permalloy (Py) are taken: saturation magnetization  A/m, exchange stiffness constant
A/m, exchange stiffness constant 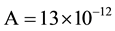 J/m. The gyromagnetic ratio
J/m. The gyromagnetic ratio 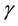 is set to be
is set to be 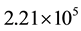 mA-1S-1 and the damping constant
mA-1S-1 and the damping constant ![]() is set to be 0.015. A cubic cell size of
is set to be 0.015. A cubic cell size of ![]() nm3 is used during the simulation. The investigated artificial square spin ice array consists 112 Pyelements, which distribute on a square lattice as shown in Figure 1(a), and each element (stadium) is of the length of
nm3 is used during the simulation. The investigated artificial square spin ice array consists 112 Pyelements, which distribute on a square lattice as shown in Figure 1(a), and each element (stadium) is of the length of ![]() nm long, of the width
nm long, of the width ![]() nm wide, of the thickness 20 nm, and the gap between neighboring elements
nm wide, of the thickness 20 nm, and the gap between neighboring elements ![]() as shown in Figure 1(b). To investigate the effect of the gap
as shown in Figure 1(b). To investigate the effect of the gap ![]() on the microwave permeability, various values of
on the microwave permeability, various values of ![]() are studied.
are studied.
3. Results and Discussion
The magnetic states of the ASI lattice are prepared by saturating the array along the (10) and the (11) directions, respectively, and then gradually decrease the external field to certain value to realize the minimization of the total energy. Two kinds of stable states of the ASI lattice RS10 and RS11 are achieved by saturating the array along the (10) and (11) directions and gradually reducing the external field to fixed value, respectively. The
![]() (a) (b)
(a) (b)
Figure 1. (a) Schematic of the investigated artificial spin ice array; (b) unit cell of the array as marked in (a) by dashed line.
magnetization distribution of the RS10 and RS11 states at zero field, for the ASI array with ![]() nm, are shown in Figure 2(a) and Figure 2(b), respectively. For the RS10 state, the magnetization orients along the + x direction for the horizontal elements, and the magnetization is not a single domain in the vertical elements of the array. In the vertical elements, the magnetization of the left and right part points to the inverse direction, respectively. For the RS11 state, the magnetization orients along the +y direction in the vertical elements and along the +x direction for the horizontal elements of the ASI array.
nm, are shown in Figure 2(a) and Figure 2(b), respectively. For the RS10 state, the magnetization orients along the + x direction for the horizontal elements, and the magnetization is not a single domain in the vertical elements of the array. In the vertical elements, the magnetization of the left and right part points to the inverse direction, respectively. For the RS11 state, the magnetization orients along the +y direction in the vertical elements and along the +x direction for the horizontal elements of the ASI array.
To investigate the effect of magnetization distribution on the microwave permeability of the ASI lattice, we firstly calculated the complex permeability of lattice with ![]() nm at RS10 and RS11 states for zero field as shown in Figure 3. For the RS10 state, the main resonance peak with the resonance frequency of 9.6 GHz can be identified with the uniform resonance mode [10] . For the RS11 state, the resonance peak locates at 9.0 GHz. This resonance mode can be attributed to the uniform resonance mode as what is observed for the RS10 state.
nm at RS10 and RS11 states for zero field as shown in Figure 3. For the RS10 state, the main resonance peak with the resonance frequency of 9.6 GHz can be identified with the uniform resonance mode [10] . For the RS11 state, the resonance peak locates at 9.0 GHz. This resonance mode can be attributed to the uniform resonance mode as what is observed for the RS10 state.
The calculated permeability and the resonance frequency as a function of the applied magnetic field strength, for the ASI array with ![]() nm, are shown in Figure 4. It is observed that both the resonance frequency and the amplitude of the imaginary part of the permeability are strongly dependent on the strength of the applied magnetic field. For the RS10 case as shown in Figure 4(a), the resonance frequency increases from 9.6 to 17.1 GHz when the applied field increases from 0 to 200 mT. While the amplitude of the imaginary part of the permeability decrease from 65.7 to 49.2. For the RS11 case as shown in Figure 4(b), the resonance frequency increases from 9.1 to 16.6 GHz when the applied field increases from 0 to 200 mT. While the amplitude of the imaginary part of the permeability decrease from 71.8 to 2.3. Therefore, the permeability of the ASI array at the
nm, are shown in Figure 4. It is observed that both the resonance frequency and the amplitude of the imaginary part of the permeability are strongly dependent on the strength of the applied magnetic field. For the RS10 case as shown in Figure 4(a), the resonance frequency increases from 9.6 to 17.1 GHz when the applied field increases from 0 to 200 mT. While the amplitude of the imaginary part of the permeability decrease from 65.7 to 49.2. For the RS11 case as shown in Figure 4(b), the resonance frequency increases from 9.1 to 16.6 GHz when the applied field increases from 0 to 200 mT. While the amplitude of the imaginary part of the permeability decrease from 71.8 to 2.3. Therefore, the permeability of the ASI array at the
![]()
![]() (a) (b)
(a) (b)
Figure 2. Magnetization distribution of the ASI lattice in the ground magnetic state with the applied field of 0 mT for (a) RS10 and RS11.
![]()
Figure 3. Calculated complex permeability of the ASI array at zero applied magnetic field for the two ground states: the solid line for RS10 and the dotted line for RS11.
RS11 state is more sensitive to the applied magnetic field with a variation of 69.5, which is much larger than that of the RS10 state of 16.5.
To investigate the effect of the gap ![]() on the permeability spectrum of the ASI array, we also calculated the permeability of ASI arrays with various
on the permeability spectrum of the ASI array, we also calculated the permeability of ASI arrays with various ![]() values at zero magnetic field. As shown in Figure 5, the permeability of the ASI array is observed to be dependent on the gap
values at zero magnetic field. As shown in Figure 5, the permeability of the ASI array is observed to be dependent on the gap ![]() values. For the RS10 case, the resonance frequency decreases from 9.6 to 9.0 GHz when the gap
values. For the RS10 case, the resonance frequency decreases from 9.6 to 9.0 GHz when the gap ![]() value increases from 130 to 230 nm. While the amplitude of the imaginary part of the permeability increase from 65.8 to 72.6. For the RS11 case as shown in Figure 5(b), the resonance frequency decreases from 9.0 to 8.8 GHz the gap
value increases from 130 to 230 nm. While the amplitude of the imaginary part of the permeability increase from 65.8 to 72.6. For the RS11 case as shown in Figure 5(b), the resonance frequency decreases from 9.0 to 8.8 GHz the gap ![]() value increases from 130 to 230 nm. While the amplitude of the imaginary part of the permeability decreases from 71.8 to 70.8. Therefore, the permeability of the ASI array at the RS10 state is more sensitive to the variation of the gap between the neighboring elements of the ASI array.
value increases from 130 to 230 nm. While the amplitude of the imaginary part of the permeability decreases from 71.8 to 70.8. Therefore, the permeability of the ASI array at the RS10 state is more sensitive to the variation of the gap between the neighboring elements of the ASI array.
4. Conclusion
In summary, the microwave complex permeability of an artificial square spin ice array is investigated using the micromagnetic simulation method. It is observed that the permeability spectrum of the ASI array exhibits different properties depending on the magnetization saturating direction. And the permeability is strongly dependent on the external applied magnetic field and the spacing gap between the comprising elements of the ASI array. Among the two studied RS10 and RS11 cases, the permeability spectrum at the RS11 state is more sensitive to the external applied magnetic field. However, the permeability spectrum at the RS10 state is more sensitive to
![]()
![]() (a) (b)
(a) (b)
Figure 4. Magnetic field strength dependence of the resonant frequency of the uniform resonance mode and the amplitude of the imaginary part of the permeability for (a) RS10 and (b) RS11.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Gap dependence of the complex permeability of the ASI array at zero applied magnetic field for the ground states: (a) RS10 and (b) RS11.
the spacing gap between the comprising elements of the ASI array. Our findings would be useful for the investigation of these novel artificial structures and their potential application for the microwave devices, i.e. tunable microwave filters working on different frequencies.