Complexity Reduced MIMO Interleaved SC-FDMA Receiver with Iterative Detection ()
1. Introduction
Recently MIMO transmission techniques with multiple transmit and receive antennas are widely used to achieve the spatially multiplexed transmission and to increase the transmission rate in wireless communications. For MIMO spatially multiplexed transmission, MLD is known as the optimum signal separation method at the receiver side, which attains the minimum BER. However, when the number of transmit antenna and the modulation levels are increased, MLD needs very high computational complexity and the reduction of complexity becomes a problem [1] - [3] . The SC-FDMA is used as the uplink wireless scheme in LTE (Long Term Evolution). The feature of its low Peak to Average Power Ratio (PAPR) characteristics decreases the burden of amplifier linearity in User Equipment (UE) and the SC-DFMA is more suitable to uplink transmission than Orthogonal Frequency Division Multiplexing (OFDM) [4] . Moreover by employing the interleaved SC-FDMA where the subcarriers for each UE are deployed like a comb tooth, the PAPR of SC-FDMA is further reduced and the frequency diversity effect becomes large. We have already proposed the MIMO SC-FDE and MIMO Interleaved SC-FDMA receivers with iterative detection where the receive signal is firstly detected by FDE, i.e., MMSE nulling, to obtain the tentative decision results and secondly the ISI cancellation from the receive signal using the tentative decision results is done followed by the MLD for separating spatially multiplexed signals [5] . However, as the complexity of MLD increases as the power of modulation levels to the number of transmit antenna, the complexity reduction of MLD becomes an important issue. For reducing the complexity of MLD, QRD-M is proposed [6] , but it is a quasi-Maximum Likelihood (ML) method and could not obtain the ML solution although the complexity is greatly reduced. On the other hand, SD [1] [2] can obtain the ML solution like MLD with reduced complexity. In this paper, we propose the novel receiver structure in which the MLD is replaced by QRD-M or SD to reduce the complexity of MLD [5] . In addition, by using RTS algorithm [7] , we add the bit LLR output function on SD, which enables the proposed SD receiver to cancel the ISI with the soft replica resulting in more accurate ISI cancellation. Moreover we have replaced the RTS by the STS [8] algorithm to further reduce the complexity of RTS. Through computer simulations, we have examined the BER characteristics and the complexity reduction effect of proposed MIMO interleaved SC-FDMA iterative receiver with ISI canceller and MLD, QRD-M, SD with RTS or STS. Consequently we verify that the receiver structure using STS mostly improves the BER and the complexity.
2. MIMO Interleaved SC-FDMA receiver
2.1. Proposed transmitter and receiver structure
In Figure 1, the block diagram of transmitter and receiver for the uplink is shown. At the transmitter of each UE, the Quadrature Amplitude Modulation (QAM) modulated signal is Fast Fourier Transform (FFT) transformed with N-points and converted to the frequency domain. The FFT points are then mapped to the interleaved frequency points like a comb tooth. After that, the frequency points are Inverse FFT (IFFT) transformed with M points (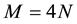 in case of 4 UE’s for example) to obtain the time domain signal. The Cyclic Prefix (CP) is inserted and the signal is transmitted to the channel. At the receiver in Base Station (BS), after removing the CP, the FDE, i.e., MMSE nulling, is firstly done. The receive signal is then FFT converted with
in case of 4 UE’s for example) to obtain the time domain signal. The Cyclic Prefix (CP) is inserted and the signal is transmitted to the channel. At the receiver in Base Station (BS), after removing the CP, the FDE, i.e., MMSE nulling, is firstly done. The receive signal is then FFT converted with 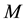 points and the frequency domain signal is obtained. The frequency points are de-mapped to each user subcarrier arrangement and the subcarriers are multiplied by the MMSE weight
points and the frequency domain signal is obtained. The frequency points are de-mapped to each user subcarrier arrangement and the subcarriers are multiplied by the MMSE weight 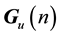 at frequency point n, i.e.
at frequency point n, i.e.
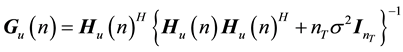 (1)
(1)
where 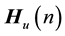 denotes the MIMO channel matrix at the frequency point
denotes the MIMO channel matrix at the frequency point  assigned to the user
assigned to the user 
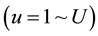 ,
, 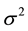 the variance of noise at each frequency point,
the variance of noise at each frequency point,  the identity matrix with the size
the identity matrix with the size 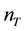 which is the number of transmit antenna. After that, the frequency points are IFFT transformed with
which is the number of transmit antenna. After that, the frequency points are IFFT transformed with 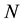 points and the time domain signal to be detected is obtained as
points and the time domain signal to be detected is obtained as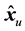 .
.
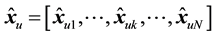 (2)
(2)
We call 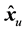 as the tentative decision through FDE. Using
as the tentative decision through FDE. Using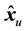 , the receive signal replica due to ISI caused by the transmit signals other than the signal at time
, the receive signal replica due to ISI caused by the transmit signals other than the signal at time ![]() to be detected, is generated and is subtracted from the receive signal. Using tentative decision result of (2) and by letting the transmit signal of user
to be detected, is generated and is subtracted from the receive signal. Using tentative decision result of (2) and by letting the transmit signal of user ![]() at time
at time ![]() being 0, the tentative decision result for ISI cancellation is obtained as (3).
being 0, the tentative decision result for ISI cancellation is obtained as (3).
![]() (3)
(3)
![]()
![]()
Figure 1. Block diagram of MIMO SC-FDMA transmitter and the proposed receiver structure with iterative feedback.
Next, ![]() in (3) is transformed to frequency domain signal of
in (3) is transformed to frequency domain signal of ![]() using FFT with
using FFT with ![]() points. The fre-
points. The fre-
quency domain ISI replica is made through multiplying ![]() by the channel matrix
by the channel matrix ![]() and the ISI
and the ISI
replica ![]() is subtracted from the receive signal in frequency domain. Accordingly, the ISI com-
is subtracted from the receive signal in frequency domain. Accordingly, the ISI com-
ponents due to the transmit signals other than time ![]() are removed. If the ISI cancellation is perfect, then the condition where only the transmit signals at time
are removed. If the ISI cancellation is perfect, then the condition where only the transmit signals at time ![]() from
from ![]() transmit antennas are transmitted to the receiver is achieved. The ISI cancelled receive signal
transmit antennas are transmitted to the receiver is achieved. The ISI cancelled receive signal ![]() in frequency domain is expressed as
in frequency domain is expressed as
![]() (4)
(4)
where ![]() is the receive signal of user
is the receive signal of user ![]() in frequency domain. Next, for
in frequency domain. Next, for ![]() in (4), the signal sepa-
in (4), the signal sepa-
ration of spatially multiplexed transmission is done using MLD. The total number of candidates of receive replica for MLD is![]() , where
, where ![]() is the modulation levels. The candidate signal for MLD in time domain
is the modulation levels. The candidate signal for MLD in time domain ![]() is obtained by letting the transmit signals all 0 except for at time
is obtained by letting the transmit signals all 0 except for at time ![]() to be detected.
to be detected.
![]() (5)
(5)
where the matrix size is![]() .
. ![]() in (5) is then FFT transformed with
in (5) is then FFT transformed with ![]() points resulting in
points resulting in![]() .
.
![]() is then multiplied by the channel matrix of
is then multiplied by the channel matrix of ![]() which is assigned for user u at frequency point n
which is assigned for user u at frequency point n
and the candidate receive replica for MLD is obtained as![]() . Then the squared distance between
. Then the squared distance between
the ISI cancelled receive signal and the candidate MLD replica in frequency domain is calculated as
![]() (6)
(6)
where ![]() denotes the Euclidian norm. (6) is minimized over the total
denotes the Euclidian norm. (6) is minimized over the total ![]() MLD candidates and the MLD
MLD candidates and the MLD
output of ![]() in (5) which minimizes (6) is obtained. The tentative decision result
in (5) which minimizes (6) is obtained. The tentative decision result ![]() in (2) is then replaced by the obtained
in (2) is then replaced by the obtained ![]() and the procedure proceeds from time
and the procedure proceeds from time ![]() to time
to time ![]() where the initial value of
where the initial value of ![]() is 1. This ISI canceller with MLD procedure is sequentially done from time 1 to
is 1. This ISI canceller with MLD procedure is sequentially done from time 1 to![]() . Accordingly the residual ISI components in tentative FDE decision results are more precisely removed and the spatially multiplexed signals are more accurately separated. After the processing for one FFT block is done, the obtained decision results for one block are regarded as the evolved tentative decision results. Then the MLD outputs are fed back to the ISI canceller at each FFT block and this feedback is iteratively done to lower the final BER.
. Accordingly the residual ISI components in tentative FDE decision results are more precisely removed and the spatially multiplexed signals are more accurately separated. After the processing for one FFT block is done, the obtained decision results for one block are regarded as the evolved tentative decision results. Then the MLD outputs are fed back to the ISI canceller at each FFT block and this feedback is iteratively done to lower the final BER.
2.2. Complexity reduction of MLD by QRD-M or SD
The number of candidate replicas in MLD increases exponentially as![]() . As the complexity reduction method of MLD, we illustrate the method utilizing the tree search of MLD with QR decomposition [6] . The receive signal vector is written as
. As the complexity reduction method of MLD, we illustrate the method utilizing the tree search of MLD with QR decomposition [6] . The receive signal vector is written as
![]() (7)
(7)
where ![]() is the receive signal vector with
is the receive signal vector with![]() ,
, ![]() the frequency flat channel matrix with
the frequency flat channel matrix with![]() ,
, ![]() the transmit signal vector with
the transmit signal vector with ![]() and
and ![]() the receive noise vector with
the receive noise vector with![]() . Using the QR decomposition, the channel matrix is decomposed into
. Using the QR decomposition, the channel matrix is decomposed into![]() , where
, where ![]() is the unitary matrix and
is the unitary matrix and ![]() is the upper triangular matrix. By multiplying the Hermitian transpose
is the upper triangular matrix. By multiplying the Hermitian transpose ![]() by
by ![]() from the left hand side, we obtain
from the left hand side, we obtain
![]() (8)
(8)
where ![]() and
and![]() . The MLD criterion is then expressed as
. The MLD criterion is then expressed as
![]() (9)
(9)
As ![]() is the upper triangular matrix, the detection of transmit signal is considered as the tree search problem from
is the upper triangular matrix, the detection of transmit signal is considered as the tree search problem from ![]() where
where ![]() denotes the transmit signal candidate from antenna
denotes the transmit signal candidate from antenna![]() . The tree structure is shown in Figure 2 when
. The tree structure is shown in Figure 2 when ![]() (BPSK) and
(BPSK) and![]() , where the diverging number at each node and the depth of tree become
, where the diverging number at each node and the depth of tree become ![]() and
and ![]() respectively. Equation (9) is also expressed in elements as
respectively. Equation (9) is also expressed in elements as
![]() (10)
(10)
As the tree search method for Figure 2 toward the width direction, ![]() algorithm is widely known. At each step, the squared distance norm for every branch is calculated, and arbitral
algorithm is widely known. At each step, the squared distance norm for every branch is calculated, and arbitral ![]() survival paths with the least cumulative squared distance metric are retained. The complexity of
survival paths with the least cumulative squared distance metric are retained. The complexity of ![]() algorithm is constant when the value of
algorithm is constant when the value of ![]() is determined and the QRD-M algorithm reduces the complexity of MLD very much, especially when
is determined and the QRD-M algorithm reduces the complexity of MLD very much, especially when![]() . But it could not obtain the ML solution, i.e., quasi-ML. On the other hand, the SD algorithm searches the tree of Figure 2 toward the depth direction. The SD first determines the initial sphere radius
. But it could not obtain the ML solution, i.e., quasi-ML. On the other hand, the SD algorithm searches the tree of Figure 2 toward the depth direction. The SD first determines the initial sphere radius ![]() for some transmit candidate of
for some transmit candidate of![]() . Next SD searches the transmit signal vector which falls within the radius
. Next SD searches the transmit signal vector which falls within the radius ![]() toward the depth direction. When the cumulative distance metric exceeds the initial radius, then the subsequent
toward the depth direction. When the cumulative distance metric exceeds the initial radius, then the subsequent
![]()
Figure 2. Tree structure of MLD when using QR decomposi- tion.
search along the path is no more needed, thus the amount of calculation is saved. Therefore, when the initial sphere radius is small, the complexity reduction becomes more effective. In other words, the higher the ![]() and the smaller the initial sphere radius is, more effectively the complexity reduction is done. If the cumulative distance metric does not exceeds the initial radius till the bottom of tree, then the initial radius is replaced by the cumulative metric and the new radius is set. In the same manner the tree search is done for every path in the tree, thus the SD can obtain the ML solution.
and the smaller the initial sphere radius is, more effectively the complexity reduction is done. If the cumulative distance metric does not exceeds the initial radius till the bottom of tree, then the initial radius is replaced by the cumulative metric and the new radius is set. In the same manner the tree search is done for every path in the tree, thus the SD can obtain the ML solution.
2.3. Receiver structure when using QRD-M algorithm
By using QRD-M instead of MLD in the receiver structure in Figure 1, we reduce the complexity of MLD. The same signal processing procedure mentioned in 2 is done to cancel the residual ISI and to satisfy the condition as if only the transmit signal at time ![]() is transmitted. After the ISI cancellation, the QRD-M is applied instead of MLD. The number of transmit signal candidates
is transmitted. After the ISI cancellation, the QRD-M is applied instead of MLD. The number of transmit signal candidates ![]() equals
equals![]() . Like in (5), the time domain transmit signal vector with
. Like in (5), the time domain transmit signal vector with ![]() points in which the candidate transmit signal is located at time
points in which the candidate transmit signal is located at time ![]() and the transmit signals at other time instants are all set to 0 is generated. Then the time domain signal vector is transformed to the frequency domain signal vector
and the transmit signals at other time instants are all set to 0 is generated. Then the time domain signal vector is transformed to the frequency domain signal vector ![]() using FFT with
using FFT with ![]() points.
points.
Then the channel matrix ![]() assigned to user
assigned to user ![]() at subcarrier number
at subcarrier number ![]() is QR decomposed.
is QR decomposed.
![]() (11)
(11)
The Hermitian transpose ![]() is multiplied by the output
is multiplied by the output ![]() of the ISI canceller from the left
of the ISI canceller from the left
hand side.
![]() (12)
(12)
The squared metric for minimization using ![]() in (12) is given by
in (12) is given by
![]() (13)
(13)
Using ![]() algorithm, (13) is step by step calculated from the bottom to the top. The
algorithm, (13) is step by step calculated from the bottom to the top. The ![]() survival paths with the least cumulative metrics are retained at each step from the bottom. The path which minimizes (13) is finally selected from the
survival paths with the least cumulative metrics are retained at each step from the bottom. The path which minimizes (13) is finally selected from the ![]() survival paths which reach the top. The path obtained by ORD-M determines the output
survival paths which reach the top. The path obtained by ORD-M determines the output![]() . The signal processing afterward is the same as MLD.
. The signal processing afterward is the same as MLD.
2.4. Receiver structure when using SD algorithm
By using SD instead of MLD in the receiver structure in Figure 1, we reduce the complexity of MLD. The same signal processing procedure mentioned in 2 is done to cancel the residual ISI and to satisfy the condition as if only the transmit signal at time ![]() is transmitted. In the proposed SD, the initial radius is set using QRD-M. (13) is used for the search of initial radius using QRD-M. The cumulative metric with small radius is firstly searched in the tree using QRD-M and we set this cumulative metric as the initial radius. Next the transmit signal candidate which satisfies the initial radius is searched toward the depth direction in the tree. When the cumulative distance metric exceeds the initial radius, then the subsequent search along the path is no more needed, thus the amount of calculation is saved. If the cumulative distance metric does not exceeds the initial radius till the bottom of tree, then the initial radius is replaced by the cumulative metric and the new radius is set. In the same manner, the tree search is done for every path in the tree, thus the SD can obtain the ML solution. In (13) the search procedure is done toward the upward direction with exhaustive search to obtain the ML solution of
is transmitted. In the proposed SD, the initial radius is set using QRD-M. (13) is used for the search of initial radius using QRD-M. The cumulative metric with small radius is firstly searched in the tree using QRD-M and we set this cumulative metric as the initial radius. Next the transmit signal candidate which satisfies the initial radius is searched toward the depth direction in the tree. When the cumulative distance metric exceeds the initial radius, then the subsequent search along the path is no more needed, thus the amount of calculation is saved. If the cumulative distance metric does not exceeds the initial radius till the bottom of tree, then the initial radius is replaced by the cumulative metric and the new radius is set. In the same manner, the tree search is done for every path in the tree, thus the SD can obtain the ML solution. In (13) the search procedure is done toward the upward direction with exhaustive search to obtain the ML solution of![]() . If the QRD-M can find a smaller initial radius, then more effectively the tree search is done.
. If the QRD-M can find a smaller initial radius, then more effectively the tree search is done.
2.5. Realization of soft output in SD
We aimed to obtain the soft output from the SD in Figure 1. In case of QPSK, the bit LLR’s for the 1st bit and the 2nd bit of the transmit signal from antenna ![]() are given by (14) and (15) respectively.
are given by (14) and (15) respectively.
![]() (14)
(14)
![]() (15)
(15)
![]() in (14) denotes the transmit signal in frequency domain of
in (14) denotes the transmit signal in frequency domain of ![]() -th user at time
-th user at time ![]() and frequency
and frequency
point ![]() from transmit antenna
from transmit antenna ![]() with the 1st bit being 0.
with the 1st bit being 0. ![]() in (14) has the same notation but with
in (14) has the same notation but with
the 1st bit being 1. ![]() and
and ![]() in (15) represent the same notation but with the 2nd bit be-
in (15) represent the same notation but with the 2nd bit be-
ing 0 and 1 respectively. In SD, there exist some paths for which searches are not made in the tree. In order to calculate the bit LLR, the path for bit “0” and the path for bit “1”, both of which have minimum path metrics, have to be evaluated. For this evaluation, we have used the RTS [7] and STS [8] algorithms.
2.6. RTS algorithm
In RTS, using (13) and the ![]() algorithm, the path with minimum path metric is obtained firstly and is regarded as the initial radius of SD. Then, the path metric which is not yet searched is calculated through SE algorithm [1] [2] . In RTS, to evaluate the bit LLR, the SE algorithm is repeatedly applied to calculate the path metric which is not searched in SD. In Figures 3(a)-(c), we show the tree structure for BPSK when the number of transmit antenna is 3, for example. In Figure 3(a), the red line shows the minimum path metric [101] obtained from the
algorithm, the path with minimum path metric is obtained firstly and is regarded as the initial radius of SD. Then, the path metric which is not yet searched is calculated through SE algorithm [1] [2] . In RTS, to evaluate the bit LLR, the SE algorithm is repeatedly applied to calculate the path metric which is not searched in SD. In Figures 3(a)-(c), we show the tree structure for BPSK when the number of transmit antenna is 3, for example. In Figure 3(a), the red line shows the minimum path metric [101] obtained from the ![]() algorithm with
algorithm with![]() . In this case, in order to obtain the bit LLR of
. In this case, in order to obtain the bit LLR of![]() , we have to find the minimum path metric for which
, we have to find the minimum path metric for which![]() , which is illustrated in Figure 3(b). Likewise, in order to obtain the bit LLR’s of
, which is illustrated in Figure 3(b). Likewise, in order to obtain the bit LLR’s of ![]() and
and![]() , we have to find the minimum path metrics for which
, we have to find the minimum path metrics for which ![]() and
and![]() , those are illustrated in Figure 3(c) and Figure 3(d) respectively. To find the minimum path metrics having the counter bits, we repeatedly use the SE algorithm.
, those are illustrated in Figure 3(c) and Figure 3(d) respectively. To find the minimum path metrics having the counter bits, we repeatedly use the SE algorithm.
2.7. STS algorithm
In STS, the path metrics for calculating the bit LLR’s are evaluated using the single search of the tree. The basic idea of STS follows that every path metric and its search depth are stored in the list and monitored. When the evolution of all the path metrics in the list does not occur during the tree search, the search of specific branch is saved and this results in complexity reduction. At the initial stage, the values in the list are all set to infinity. In Figure 4, we show the STS algorithm where the number of transmit antenna is 4, the number of modulation level![]() ,
, ![]() the accumulated norm with the search depth
the accumulated norm with the search depth ![]() and the symbol number
and the symbol number![]() ,
, ![]() the accumulated norm of ML sequence. Also, the list as an example is illustrated in Figure 5 where the number of transmit antenna is 4 and the QPSK modulation is used.
the accumulated norm of ML sequence. Also, the list as an example is illustrated in Figure 5 where the number of transmit antenna is 4 and the QPSK modulation is used.
In STS algorithm, the list in Figure 5 is filled up with the algorithm in Figure 4. When ![]() is calculated for
is calculated for
example, its value is compared with all ![]() already stored in the list. At this stage, when
already stored in the list. At this stage, when![]() , we
, we
find that the further search of this branch does not lead to the evolution of the path metric. Accordingly we stop
the search and move to the calculation of![]() . When
. When ![]() is finally obtained, the needed norms are read from
is finally obtained, the needed norms are read from
the list and the bit LLR’s are calculated using (14) and (15).
3. Computer simulation results
Computer simulations are made for the system in Figure 1. The simulation conditions are listed in Table 1. Figure 6 shows the BER characteristics when the hard decision replica is used to cancel the ISI through MLD, QRD-M or SD for spatial de-multiplexing. In Figure 6, #4, for example, denotes the number of MLD, QRD-M or SD iterated. Figure 7 shows the BER characteristics when the soft decision replica is used to cancel the ISI through RTS or STS for spatial de-multiplexing. In Figure 8, we compared the BER characteristics between hard replica cancellation and soft replica cancellation with iteration being used. Also in Figure 6-8, we showed
![]()
Figure 5. Example of list with 4 transmit antennas and the modulation level K.
![]()
Figure 6. Comparison of BER characteristics of MIMO inter- leaved SC-FDMA receiver with hard replica cancellation of ISI.
![]()
Figure 7. Comparison of BER characteristics of MIMO inter- leaved SC-FDMA receiver with soft replica cancellation of ISI.
![]()
Figure 8. Comparison of BER characteristics of MIMO inter- leaved SC-FDMA receiver between hard decision and soft de- cision with iterative feedback.
the lower bound of BER where the ISI cancellation is perfect, which means the demodulated bits for ISI cancellation are error-free. In Figure 9, we show the comparison of complexity of MLD, QRD-M, SD, RTS and STS on ![]() flat fading channel. This complexity is measured using “tic” and “toc” function in MATLAB and the computation time needed for MLD is normalized to unity.
flat fading channel. This complexity is measured using “tic” and “toc” function in MATLAB and the computation time needed for MLD is normalized to unity.
From Figure 6, compared with the conventional FDE receiver, the proposed receiver using MLD with no iterative feedback improves the BER by about 7 dB at![]() . By increasing the number of iterative feedbacks, the proposed receiver further improves the BER and obtains the BER improvement of more than 10 dB which is close to the lower bound of BER. This is because the MLD outputs with high reliability are used as the improved decision results for making the accurate ISI replicas. Accordingly more exact ISI cancellation becomes possible followed by improved MLD performance. We observe the BER performance of QRD-M is inferior to MLD, but the BER of SD coincides with the MLD, thus the SD can obtain the ML solution.
. By increasing the number of iterative feedbacks, the proposed receiver further improves the BER and obtains the BER improvement of more than 10 dB which is close to the lower bound of BER. This is because the MLD outputs with high reliability are used as the improved decision results for making the accurate ISI replicas. Accordingly more exact ISI cancellation becomes possible followed by improved MLD performance. We observe the BER performance of QRD-M is inferior to MLD, but the BER of SD coincides with the MLD, thus the SD can obtain the ML solution.
From Figure 7, we see that the BER performance with soft ISI cancellation behaves basically the same as the SD with hard ISI cancellation in Figure 6, but the BER approaches more rapidly to the lower bound than the
hard ISI cancellation. We find that at average ![]() the BER coincides with the lower bound and
the BER coincides with the lower bound and
this means the perfect ISI cancellation is possible at this receive SNR value.
From Figure 8, we see that the soft ISI cancellation with iterative feedback performs better than the hard replica cancellation. This is because more accurate ISI replica for cancellation can be generated for the soft decision than the hard decision.
From Figure 9, QRD-M, SD, RTS and STS can reduce the computation time compared with MLD. The QRD- M is the most effective in reducing the computation time. The computation time is almost 1/100 of MLD and is constant over the average ![]() value. However, QRD-M is sub-optimal and ML solution is not obtained. The SD can obtain the ML solution, but for low average
value. However, QRD-M is sub-optimal and ML solution is not obtained. The SD can obtain the ML solution, but for low average ![]() region less than 10 dB the computation
region less than 10 dB the computation
![]()
Figure 9. Comparison of computation time among MLD, QRD- M, SD, RTS and STS on flat fading channel.
time is about 15 times higher than QRD-M. However, above![]() , the computation time ap-
, the computation time ap-
proaches to QRD-M. This is because for high average ![]() region, the initial radius can be set to a very
region, the initial radius can be set to a very
small value. Although the RTS can produce the soft output, the RTS needs a lot of path metric calculation leading relatively high computation time. The STS which is the improved version of RTS shows the computation
time almost the same as the SD in low ![]() region. Therefore it can reduce the computation time about 1/5
region. Therefore it can reduce the computation time about 1/5
compared with the RTS. However, the computation time of STS is almost constant over entire ![]() region.
region.
4. Conclusion
In this paper, we have proposed the low BER receiver structure for the interleaved SC-FDMA on the uplink MIMO frequency selective fading channels. In the proposed receiver, using the tentative decision results obtained from the MMSE nulling (FDE), the ISI components are cancelled and the MLD is then used for separating the spatially multiplexed signal streams. The reliable output from MLD is again fed back to the ISI canceller to reduce the residual ISI. Furthermore we improve the complexity of MLD by replacing it with QRD-M or SD. We have verified the BER characteristics of the proposed receiver with MLD, QRD-M or SD through computer simulations. The receiver with SD achieves the same BER as the one with MLD, i.e., ML solution, whereas the QRD-M has the inferior BER because of its quasi-ML solution. We have also verified that the complexity of SD is very much improved compared with MLD especially in high ![]() region. In order to cancel the ISI more effectively using soft replica, we have further replaced the SD by RTS or STS algorithm in which the soft out from SD is available. As a result, the BER characteristic approaches more rapidly to the lower bound. The complexity of STS is lower than the RTS and almost coincides with the SD in low
region. In order to cancel the ISI more effectively using soft replica, we have further replaced the SD by RTS or STS algorithm in which the soft out from SD is available. As a result, the BER characteristic approaches more rapidly to the lower bound. The complexity of STS is lower than the RTS and almost coincides with the SD in low ![]() region. The proposed receiver structure will be useful to extend the coverage of uplink.
region. The proposed receiver structure will be useful to extend the coverage of uplink.
Acknowledgements
This study has been supported by the Scientific Research Grant-in-aid of Japan No. 24560454 and Sharp cooperation.