1. Introduction
In recent years, major distribution companies of information goods have developed technological tools known as digital rights management (DRM) to prevent the copying of their goods. However, these tools have a negative impact on consumer usage of original information goods because they hinder their use. For instance, DRM for music can limit the use of music files downloaded from online retailers, the number of computers to which the user can transfer his or her files and the number of times a playlist can be burned on a CD-R (Duchêne and Waelbroeck [1] ). However, the latest technological developments and the Internet have enabled consumers to overcome these restrictions so that consumers are able to learn by copying, to the point where it is possible that some consumers may prefer a copy to an original because they can use the copy more easily and in more devices and even improve its quality.
Copying technology by consumers is showing increasing returns to scale as analyzed by Belleflamme and Picard [2] 1. They show that the multiproduct monopolist has a greater incentive to set lower prices than the duo- polist because decreasing the price for one good increases demand for the other good by making copying less attractive. They call this result the Cournot effect. Finally, Belleflamme and Picard [2] show that a multiproduct monopoly provides greater welfare than a duopoly in the short run but provides lower incentives to create new goods in the long run.
The theoretical literature devoted to analyze the causes and consequences of piracy is extensive and it is divided into two parts: i) when the copies are made by consumers, which refer to noncommercial copying by final consumers, and ii) when firms illegally makes copies and sells them on the market, which is known as commercial piracy2. In this paper, we focus on end-user copying and analyze the process of learning by copying by consumers where they are able to make better copies as they make more, to the point that they may come to value copies more highly than originals3. We find that when the effect of learning by copying is strong and the cost of copying is low enough, consumers decide to copy all goods, even if they are given away for free. This suggests that DRM systems implemented by the digital industry have adverse consequences because they hinder the use of original goods and encourage consumers to copy. Moreover, we show that the existence of the Cour- not effect may fail, unlike previous studies. Finally, by analyzing social welfare we show that the results ob- tained by Belleflamme and Picard [2] are robust when we consider a more general cost function of copying.
The rest of the paper is organized as follows. Section 2 describes the model. Section 3 considers that both goods are sold by a multiproduct monopolist. Section 4 analyzes the duopoly case. Section 5 analyzes social welfare. Finally, Section 6 concludes.
2. The Model
There are two goods,  and
and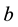 , which are independent of each other. We assume that there are two consumers who value goods differently, although each consumer values each good in the same way, as in Belleflamme and Picard [2] . Let
, which are independent of each other. We assume that there are two consumers who value goods differently, although each consumer values each good in the same way, as in Belleflamme and Picard [2] . Let 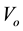
 and
and 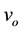
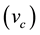 be the valuation of consumers 1 and 2 of any original good (copy), respectively. With no loss of generality, we assume that consumer 1 values any good more highly depending on whether it is an original or a copy, i.e.
be the valuation of consumers 1 and 2 of any original good (copy), respectively. With no loss of generality, we assume that consumer 1 values any good more highly depending on whether it is an original or a copy, i.e. 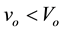 and
and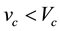 .
.
Let c be the cost of copying a good by consumers. We represent the process of learning by copying as an increase in the valuation of the second copy made by consumers, which we call the gain of the second copy and represent by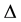 . We do not represent the process of learning by copying through the cost of copying, although our analysis is equivalent to this if we define the cost of the first copy as
. We do not represent the process of learning by copying through the cost of copying, although our analysis is equivalent to this if we define the cost of the first copy as 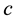 and the cost of the second copy as
and the cost of the second copy as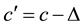 . Notice that the last cost function of copying can be decreasing, constant or increasing in the number of copies made by consumers, according to the value of the gain of the second copy,
. Notice that the last cost function of copying can be decreasing, constant or increasing in the number of copies made by consumers, according to the value of the gain of the second copy,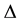 . Given that we are interested in analyzing the effect of copying by consumers, we assume that they always prefer to copy a good over not buying it, so that
. Given that we are interested in analyzing the effect of copying by consumers, we assume that they always prefer to copy a good over not buying it, so that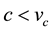 . Thus, the utility of consumer 1 is:
. Thus, the utility of consumer 1 is:
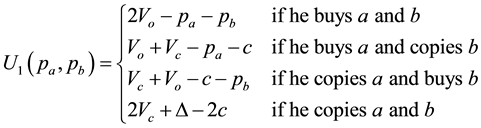 (1)
(1)
where  is the price of good
is the price of good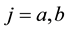 . We obtain the utility of consumer 2 in the same way, but take into account that he values the original good at
. We obtain the utility of consumer 2 in the same way, but take into account that he values the original good at ![]() and the copy at
and the copy at![]() . To prevent problems with the existence of equilibrium, we assume that, when a consumer is indifferent to buying or copying a good, he decides to buy it.
. To prevent problems with the existence of equilibrium, we assume that, when a consumer is indifferent to buying or copying a good, he decides to buy it.
Let ![]() and
and ![]() be the valuation gap for consumers 1 and 2 between any original good and its copy, respectively. We assume that
be the valuation gap for consumers 1 and 2 between any original good and its copy, respectively. We assume that![]() . This implies that the maximum price that consumer 1 is willing to pay for any original good
. This implies that the maximum price that consumer 1 is willing to pay for any original good ![]() is higher than that of consumer 2
is higher than that of consumer 2![]() , which is in keeping with the fact that consumer 1 values goods more highly.
, which is in keeping with the fact that consumer 1 values goods more highly.
An interesting result is that when![]() , consumers decide to copy all goods, even if they are given away for free. This suggests that the DRM systems implemented by the digital industry to prevent consumers from copying goods have the adverse effect of destroying demand for original goods. Thus, we assume that
, consumers decide to copy all goods, even if they are given away for free. This suggests that the DRM systems implemented by the digital industry to prevent consumers from copying goods have the adverse effect of destroying demand for original goods. Thus, we assume that ![]() to guarantee that any consumer strategy could be optimal.
to guarantee that any consumer strategy could be optimal.
By comparing the levels of utility obtained by each consumer we find the demand for goods, which is illu- strated in Figure 1. ![]()
![]() means that consumer
means that consumer ![]() buys (copies) product
buys (copies) product![]() . Note that the pro-
. Note that the pro-
![]() (a) (b)
(a) (b)
Figure 1. The demand for goods. (a) Δ ≤ δV − δv; (b) δV − δv ≤ Δ < c + δv.
cess of learning by copying makes goods complementary for certain prices, although they are independent in content.
3. Multiproduct Monopoly
Given that we have assumed that the production cost is zero, the monopolist prefers to sell a good over not sell- ing it. Thus, those outcomes where a good is copied by all consumers are not equilibria. In this way, the mono- polist will set the maximum price for each good that makes consumers indifferent between buying and copying it. Therefore, the candidate strategies for equilibrium are in Table 14.
As we can see in the following proposition, the optimal decision of the monopolist depends on how much consumer 2 is willing to pay for each good. Thus, when consumer 2 is willing to pay enough for each good, the monopolist sells to both consumers. Otherwise, the monopolist sells only to consumer 1.
Proposition 1 In any subgame perfect equilibrium, it follows that:
1. if![]() , the optimal strategy is (iii); and
, the optimal strategy is (iii); and
2. if![]() , the optimal strategy is (i).
, the optimal strategy is (i).
Proof: see Appendix.
4. Duopoly
Given that in a duopoly there is multiplicity of equilibria, let us assume that firms always choose a symmetrical undominated subgame perfect equilibrium (SUSPE) in our game. Thus, SUSPE are those equilibria that provide a maximal joint profit. As can be seen in the following proposition, the equilibrium where consumer 1 buys both goods and consumer 2 copies them is SUSPE if and only if![]() ; otherwise, the equilibrium where both consumers buy both goods is SUSPE.
; otherwise, the equilibrium where both consumers buy both goods is SUSPE.
Proposition 2 The SUSPE, independent of the size of the gain on the second copy, is:
1.![]() , with
, with![]() , if
, if![]() ; and
; and
2.![]() , with
, with![]() , if
, if![]() .
.
Proof: see Appendix.
By comparing SUSPE under a monopoly and a duopoly, we find that the “Cournot effect” only exists when![]() . This effect means that the monopolist sets a lower average price than the duopolist because he knows that the two goods are complementary, i.e. decreasing the price for one good in- creases demand for the other. This result differs from that obtained by Belleflamme and Picard [2] , who find that the Cournot effect always exists. Thus, the existence of the Cournot effect depends on
. This effect means that the monopolist sets a lower average price than the duopolist because he knows that the two goods are complementary, i.e. decreasing the price for one good in- creases demand for the other. This result differs from that obtained by Belleflamme and Picard [2] , who find that the Cournot effect always exists. Thus, the existence of the Cournot effect depends on ![]() and
and![]() .
.
![]()
Table 1. Candidate strategies for equilibrium.
5. Welfare Analysis
Belleflamme and Picard [2007] show that from a static perspective the multiproduct monopoly provides greater welfare than the duopoly, but from a dynamic perspective the duopoly provides greater incentives to create a new good than the monopoly. In order to provide clearer, more relevant conclusions, we consider SUSPE.
Ex post efficiency
In both a monopoly and a duopoly there are two possible outcomes: firstly, where consumer 1 buys both goods and consumer 2 copies them (represented by subscript c); and secondly, where both consumers buy both goods (represented by subscript b). We define social welfare as the sum of firms’ profits and consumer surplus. Thus, from the results obtained in Proposition 1 and in Proposition 2 we deduce that social welfare in a monopoly and a duopoly is
![]() (2)
(2)
![]() (3)
(3)
where ![]() and
and![]() . We can see that
. We can see that ![]() if and only if
if and only if![]() , which is always satisfied because we assume that
, which is always satisfied because we assume that![]() . If we compare social welfare in a monopoly and in a duopoly, we can see that the former is at least as great as the latter, as shown by Belleflamme and Picard [2] .
. If we compare social welfare in a monopoly and in a duopoly, we can see that the former is at least as great as the latter, as shown by Belleflamme and Picard [2] .
Proposition 3 In any SUSPE, we have that![]() .
.
Ex ante efficiency
To check that a duopolist has more incentives to create a new good, we must check that![]() , where
, where ![]() is the duopolist’s profit and
is the duopolist’s profit and ![]() is the monopolist’s incentive to create a new product, where
is the monopolist’s incentive to create a new product, where ![]() is the profit of a multiproduct monopolist and
is the profit of a multiproduct monopolist and ![]() is the profit of a monopolist that sells only one product.
is the profit of a monopolist that sells only one product.
![]() (4)
(4)
We show that an entrant has higher incentives to create a new good than a monopolist, as in Belleflamme and Picard [2] .
Proposition 4 An entrant has higher incentives to create a new product than a multiproduct monopolist.
Proof: see Appendix.
6. Conclusions
We have developed a model that lets us analyze the behaviour of a multiproduct monopolist, a duopolist and consumers who are able to learn by copying. We have shown that the DRM systems implemented by the digital industry have adverse consequences because they hinder the use of original goods and provide consumers with an incentive for copying.
Unlike Belleflamme and Picard [2] , we have shown that the existence of the Cournot effect depends on the size of the gain on the second copy and the quantity that the consumer, who least values the goods, is willing to pay for each. However, like Belleflamme and Picard [2] , we have shown that a monopoly will provide greater welfare than a duopoly in the short run but provide lower incentives to create new products in the long run.
Acknowledgements
I would like to thank my advisor Javier M. López-Cuñat for his helpful and invaluable guidance and patience. I am also grateful for useful comments and suggestions from Ramón Fauli-Oller, Nikolaos Georgantzis, María José Gil-Moltó, Inés Macho-Standler, Joel Sandonís and an anonymous referee. I acknowledge the financial support from the Spanish Ministerio de Economa y Competitividad, under projects ECO2010-19830 and ECO2013-45698. Any remaining errors are mine alone.
Appendix
Proof of Proposition 1. We get:
1.![]() ; iff
; iff![]() ,
,
2.![]() , iff
, iff![]() ; and
; and
3.![]() , iff
, iff![]() .
.
Proof of Proposition 2. When the gain on the second copy is low enough, i.e.![]() , the reaction function of firm
, the reaction function of firm![]() , when
, when![]() , is:
, is:
![]() (5)
(5)
when![]() , is:
, is:
![]() (6)
(6)
when![]() , is:
, is:
![]() (7)
(7)
and when![]() , is:
, is:
![]() (8)
(8)
From the intersection of reaction functions we obtain the equilibrium, which is shown in Figure A1.
We now consider that the gain on the second copy is high enough, i.e.![]() . Thus, relationship (9) holds:
. Thus, relationship (9) holds:
![]() (9)
(9)
Therefore, the reaction function of firm![]() , when
, when ![]() is:
is:
![]() (10)
(10)
when![]() , is:
, is:
![]()
Figure A1. Equilibrium when the gain on the second copy is low enough.
![]() (11)
(11)
when![]() , is:
, is:
![]() (12)
(12)
and when![]() , is:
, is:
![]() (13)
(13)
From the intersection of reaction functions we obtain the equilibrium, which is shown in Figure A2.
Proof of Proposition 4.
1. If![]() , we have
, we have![]() ,
, ![]() and
and![]() . Thus,
. Thus,![]() .
.
2. If![]() , we have
, we have![]() ,
, ![]() and
and![]() . Thus,
. Thus,![]() .
.
![]()
Figure A2. Equilibrium when the gain on the second copy is high enough.
3. If![]() , we have
, we have![]() ,
, ![]() and
and ![]() . Thus,
. Thus,![]() .
.
4. if![]() , we have
, we have![]() ,
, ![]() and
and![]() . Thus,
. Thus,![]() .
.
NOTES
1Martínez-Sánchez [3] uses the model developed by Belleflamme and Picard [2] for investigating the firms’ ability to tacitly collude on prices in an infinitely repeated duopoly game of vertical product differentiation.
![]()
2Recent papers on commercial piracy are Martínez-Sánchez ([4] [5] ) and López-Cuñat and Martínez-Sánchez [6] .
3Peitz and Waelbroeck [7] and Belleflamme and Peitz [8] provide surveys of the theoretical literature of piracy, while Dejean [9] provides a survey of the empirical literature.
![]()
4Notice that the candidate strategy ![]() is not included in Table 1 because it is equivalent to strategy (ii).
is not included in Table 1 because it is equivalent to strategy (ii).