Energy-Minimizing Curve Fitting for High-Order Surface Mesh Generation ()
1. Introduction
The present work is motivated by curvilinear mesh generation for high-order numerical methods such as spectral and hp element methods [1] [2] or discontinuous Galerkin methods [3] [4] . Exploiting the superior convergence properties of these methods for problems of practical interest requires an accurate and well behaved piecewise polynomial representation of complex domains including their boundaries. Unfortunately, contemporary state- of-the-art mesh generators are tailored to low-order discretization methods and, hence, provide only piecewise linear or quadratic meshes. Consequently, various approaches were developed for converting straight meshes into curvilinear ones [5] . Recently, considerable effort has been dedicated to assure the validity and to improve the quality of the curved mesh [6] - [8] . Most of this work deals with situations where the mesh spacing is smaller
or of the same size as the radius of curvature, often in conjunction with a moderate polynomial degree. To the best of our knowledge, the generation of suitable meshes with higher order (say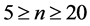 ) and spacings exceeding the radius of curvature still remains a challenge.
) and spacings exceeding the radius of curvature still remains a challenge.
As a first step of curvilinear mesh generation we consider the construction of polynomial curves from a given straight-sided surface mesh. This problem can be regarded as a special case of curve fitting, which, in turn, is a well established research area in computer aided geometric design [9] [10] . Typically the sought curve is not fitted to the surface as such, but to a set of samples extracted from the latter. A widespread approach is to use splines in tension or smoothing splines, which attain a fair shape by minimizing a certain energy functional related to stretching, bending, twist, or a combination thereof [9] . Veltkamp and Wesselink [11] explored these and a variety of related energy functionals in fitting B-splines to a set of given points in 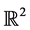 or
or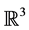 . Higher-order curves such as B-splines are often computed by minimizing an error functional augmented by a suitable energy measure for regularization [12] . Unfortunately, the energy functional tends to act diametrically to the error functional and thus prevents convergence to the exact surface with increasing polynomial order. As an alternative Alhanaty and Bercovier [13] proposed the use of optimal control methods for constructing interpolating splines with minimal energy. Apart from the advantage of guaranteeing optimality, this approach implies that the number of samples does not exceed the degree of freedom available for fitting, which may prove too restrictive for many applications. Flöry and Hofer [14] advocated an incremental strategy for fitting curves on manifolds using a weighted average of error and energy functionals as the objective function. In course of their iterative procedure the weight of energy is successively reduced, thus improving the accuracy of the final curve. It should be remarked, however, that this method is not intended for generating energy-minimized curves. Indeed, the curve energy is essentially determined by the chosen sample points, which remain fixed throughout the fitting procedure. A direct approach to energy-minimizing splines was developed by Hofer and Pottmann [15] [16] . The key idea consists in translating the sample points tangentially on the given manifold until the imposed energy functional attains a minimum. This process is embedded in an iterative procedure which constrains the movement of samples to a trust region. More precisely, the method does not minimize the curve energy, but a finite difference approximation of the latter based on the sample points. The optimality of the resulting curve will therefore depend on the sampling density. Finally we remark that curvature minimizing smoothing offers a powerful alternative to fitting worth considering especially with noisy surface data, see e.g. [17] and references therein.
. Higher-order curves such as B-splines are often computed by minimizing an error functional augmented by a suitable energy measure for regularization [12] . Unfortunately, the energy functional tends to act diametrically to the error functional and thus prevents convergence to the exact surface with increasing polynomial order. As an alternative Alhanaty and Bercovier [13] proposed the use of optimal control methods for constructing interpolating splines with minimal energy. Apart from the advantage of guaranteeing optimality, this approach implies that the number of samples does not exceed the degree of freedom available for fitting, which may prove too restrictive for many applications. Flöry and Hofer [14] advocated an incremental strategy for fitting curves on manifolds using a weighted average of error and energy functionals as the objective function. In course of their iterative procedure the weight of energy is successively reduced, thus improving the accuracy of the final curve. It should be remarked, however, that this method is not intended for generating energy-minimized curves. Indeed, the curve energy is essentially determined by the chosen sample points, which remain fixed throughout the fitting procedure. A direct approach to energy-minimizing splines was developed by Hofer and Pottmann [15] [16] . The key idea consists in translating the sample points tangentially on the given manifold until the imposed energy functional attains a minimum. This process is embedded in an iterative procedure which constrains the movement of samples to a trust region. More precisely, the method does not minimize the curve energy, but a finite difference approximation of the latter based on the sample points. The optimality of the resulting curve will therefore depend on the sampling density. Finally we remark that curvature minimizing smoothing offers a powerful alternative to fitting worth considering especially with noisy surface data, see e.g. [17] and references therein.
In this paper we investigate techniques for fitting Bézier curves to surfaces for application with high-order mesh generation. Starting from squared distance minimization we develop an incremental algorithm leading to an accurate, energy-minimizing method that combines the ideas put forward in [14] [15] . The paper is organized as follows: In Section 2 we first revisit least-squares fitting and then elaborate the energy-minimizing curve fitting procedure. Section 3 provides a comparison of both methods covering analytically defined smooth surfaces as well as scattered surface data. Section 4 concludes the paper.
2. Surface Curve Construction
In spectral or hp element methods, each element face coinciding with the domain boundary constitutes a polynomial surface patch. Therefore, the construction of well behaved polynomial patches represents a natural building block in curvilinear mesh generation. Starting from a straight-sided initial mesh, the curvilinear mesh is often built in a hierarchical process consisting of the following steps: i) construction of boundary curves representing the edges of the boundary faces; ii) generation of patches defining the boundary faces; and iii) creation of curved volume elements. Here we focus on the first step, the construction of high-order polynomial boundary curves. Adopting the Bézier form, a curve of order  is expressed as
is expressed as
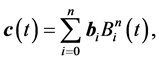 (1)
(1)
where  are the Bernstein polynomials and
are the Bernstein polynomials and 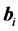 the corresponding control points. For convenience we assume that the vertices of the initial mesh and, hence, the start and end points of the curves are fixed and given such that they fit to the boundary surface.
the corresponding control points. For convenience we assume that the vertices of the initial mesh and, hence, the start and end points of the curves are fixed and given such that they fit to the boundary surface.
2.1. Distance-Based Curve Fitting
Curve fitting is used to construct a boundary edge  between vertices
between vertices 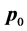 and
and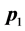 . For this purpose we perform a least squares fitting to a set of sampling points generated from the initial, linear edge.
. For this purpose we perform a least squares fitting to a set of sampling points generated from the initial, linear edge.
The procedure starts with the selection of 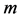 samples
samples 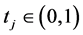 in parameter space. Next, a corresponding point distribution is generated on the straight edge by means of linear interpolation. Projecting these points to the boundary surface yields the sampling points
in parameter space. Next, a corresponding point distribution is generated on the straight edge by means of linear interpolation. Projecting these points to the boundary surface yields the sampling points
 (2)
(2)
where, ideally, the operator 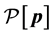 represents the normal projection of a given point
represents the normal projection of a given point 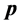 to a surface point
to a surface point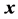 . In practice the projection is realized by means of an iterative procedure based on the approximate normal vector. In case of scattered data, we use a fine triangulation combined with a smoothing interpolation as the surface definition. Fitting is performed by minimizing the average squared distance
. In practice the projection is realized by means of an iterative procedure based on the approximate normal vector. In case of scattered data, we use a fine triangulation combined with a smoothing interpolation as the surface definition. Fitting is performed by minimizing the average squared distance
![]() (3)
(3)
where ![]() denotes set of the interior control points of the curve,
denotes set of the interior control points of the curve, ![]() the set samples in parameter space and
the set samples in parameter space and ![]() the corresponding set of surface points. Since the number of samples typically exceeds the degrees of freedom, the minimization problem is solved using the least-squares method, which yields the interior control points
the corresponding set of surface points. Since the number of samples typically exceeds the degrees of freedom, the minimization problem is solved using the least-squares method, which yields the interior control points ![]() of the curve
of the curve![]() .
.
2.2. Energy-Minimizing Curve Fitting
With coarse meshes purely distance-based fitting can lead to severe undulations in regions of high curvature. As a remedy one may look for curves that minimize a certain energy functional. Here we consider the ![]() norms of the first and second derivative of
norms of the first and second derivative of![]() :
:
![]() (4)
(4)
![]() (5)
(5)
The norm of the first derivative (4) is related to the elastic stretch energy of a string [11] . A surface curve which minimizes ![]() represents the shortest path between between the two endpoints and is called a geodesic. Geodesics are regularly applied in computer vision, image processing and motion design [16] . It is worth noting that the functional
represents the shortest path between between the two endpoints and is called a geodesic. Geodesics are regularly applied in computer vision, image processing and motion design [16] . It is worth noting that the functional ![]() also improves the curve towards an isometric parametrization. The norm of the second derivative (5) corresponds to bending or strain energy. Minimizing
also improves the curve towards an isometric parametrization. The norm of the second derivative (5) corresponds to bending or strain energy. Minimizing ![]() is a fundamental ingredient in cubic spline interpolation. The combination of both energies leads to the concept of splines in tension (see, e.g. [9] ). We use
is a fundamental ingredient in cubic spline interpolation. The combination of both energies leads to the concept of splines in tension (see, e.g. [9] ). We use ![]() and
and ![]() for augmenting the error functional (3), leading to the objective function
for augmenting the error functional (3), leading to the objective function
![]() (6)
(6)
where overbars indicate the normalization which has been introduced to compensate possible differences in the order of magnitude between the individual terms. In particular we define
![]() (7)
(7)
and
![]() (8)
(8)
where the superscript “0” refers to the curve obtained from distance-based fitting and “lin” to the straight edge. Note that ![]() equals the squared length of the latter, whereas
equals the squared length of the latter, whereas ![]() is identical to zero. As these two cases are close to the extrema that are to be expected in the fitting process, the normalized distance and error functionals vary typically between zero and one. The parameter
is identical to zero. As these two cases are close to the extrema that are to be expected in the fitting process, the normalized distance and error functionals vary typically between zero and one. The parameter ![]() represents the relative weight of the energy functionals compared to the error functional, while the value of
represents the relative weight of the energy functionals compared to the error functional, while the value of ![]() determines the blend of bending and stretch energy to be used in the former. Hence, applying
determines the blend of bending and stretch energy to be used in the former. Hence, applying ![]() with
with ![]() is equivalent to distance-based fitting, whereas choosing any
is equivalent to distance-based fitting, whereas choosing any ![]() and thus taking into account the curve energies leads to smoother and shorter curves but allows for deviation from the surface.
and thus taking into account the curve energies leads to smoother and shorter curves but allows for deviation from the surface.
To obtain fair surface curves we employ an incremental approach, which is outlined in Algorithm 1. The basic idea is to start fitting with a high energy weight, which is successively reduced according to a generic shape function![]() , until reaching the minimum value in the final step (line 8). Furthermore, the sampling points are recomputed from the current curve (line 9) before performing the next fitting (line 10). In this manner, curve and surface points move towards each other in course of the process, the former approaching the surface, the latter converging to an energetically improved configuration.
, until reaching the minimum value in the final step (line 8). Furthermore, the sampling points are recomputed from the current curve (line 9) before performing the next fitting (line 10). In this manner, curve and surface points move towards each other in course of the process, the former approaching the surface, the latter converging to an energetically improved configuration.
Throughout the present study we used the shape function
![]() (9)
(9)
which starts with 1 at ![]() followed by a gradual transition to 0 at
followed by a gradual transition to 0 at![]() . This choice always recovers the straight edge in the first step. Note that the final curve minimizes the mean quadratic error as well as the energy, since it results from distance-based fitting to optimized sampling points. Various other choices for the shape function
. This choice always recovers the straight edge in the first step. Note that the final curve minimizes the mean quadratic error as well as the energy, since it results from distance-based fitting to optimized sampling points. Various other choices for the shape function ![]() are possible, but have not been explored yet.
are possible, but have not been explored yet.
3. Results
In the following we study the performance of the energy-minimizing fitting method in two different cases. As the first case we consider a coarse, but nearly uniform triangulation of an explicitly defined screw surface. In the second case the “exact” surface is defined as a patchwork of cubic triangles based on a fine mesh derived from CT scans of a rabbit aorta. For assessment we use the ![]() error evaluated over all mesh curves
error evaluated over all mesh curves
![]() (10)
(10)
and the curve energy norms
![]() (11)
(11)
![]()
Algorithm 1.Incremental energy-minimizing curve fitting starting from linear edge![]() .
.
where again ![]() corresponds to stretch energy and
corresponds to stretch energy and ![]() to bending energy. The integrals in Equation (10) were computed by means of Gauss quadrature using
to bending energy. The integrals in Equation (10) were computed by means of Gauss quadrature using ![]() points.
points.
3.1. Analytically Defined Smooth Surface
As a first test case we consider the screw surface defined by the analytical expression
![]() (12)
(12)
The projection ![]() of a given point
of a given point ![]() onto the surface is realized by means of the iterative procedure
onto the surface is realized by means of the iterative procedure
![]() (13)
(13)
starting with![]() . We remark that this scheme results from a linearised solution of exact condition
. We remark that this scheme results from a linearised solution of exact condition![]() , where
, where ![]() is the surface normal vector. Figure 1 shows the exact surface in the interval
is the surface normal vector. Figure 1 shows the exact surface in the interval ![]() along with a coarse uniform triangulation. The mesh consists of 32 triangles and has an average spacing of
along with a coarse uniform triangulation. The mesh consists of 32 triangles and has an average spacing of ![]() times the minimum curvature radius,
times the minimum curvature radius,![]() .
.
The energy-minimizing fitting procedure was examined over a wide range of polynomial degrees, ranging from ![]() to 20. As an example we consider the case
to 20. As an example we consider the case![]() . Figure 2 illustrates the influence of the energy blending parameter
. Figure 2 illustrates the influence of the energy blending parameter ![]() and the number of fitting steps
and the number of fitting steps ![]() on the error
on the error ![]() and the energy norms
and the energy norms ![]() and
and![]() . The graphs correspond to three different energy compositions in the objective function:
. The graphs correspond to three different energy compositions in the objective function: ![]() implies using only stretch energy
implies using only stretch energy![]() ,
, ![]() only bending energy
only bending energy ![]() and
and ![]() an equal mixture of both. Note that the plot does not show stepwise progress, but only the characteristics of the final curve. The case
an equal mixture of both. Note that the plot does not show stepwise progress, but only the characteristics of the final curve. The case ![]() is equivalent to single-step distance-based fitting. Increasing the number of fitting steps reduces the curve energy rapidly until approximately
is equivalent to single-step distance-based fitting. Increasing the number of fitting steps reduces the curve energy rapidly until approximately![]() . In the present example, this improvement is accompanied by a slight increase in the error, which lessens with growing
. In the present example, this improvement is accompanied by a slight increase in the error, which lessens with growing![]() . We remark, however, that with finer meshes the energy-minimizing fitting succeeded in reducing the error simultaneously with the curve energy.
. We remark, however, that with finer meshes the energy-minimizing fitting succeeded in reducing the error simultaneously with the curve energy.
Figure 2 indicates that the incremental method improves both energies, even if one is excluded from the objective function by the particular choice of![]() . However, with higher
. However, with higher ![]() the excluded energy may increase slightly in favor of a further error reduction. In the present example such behavior is observed with
the excluded energy may increase slightly in favor of a further error reduction. In the present example such behavior is observed with ![]() for
for ![]() and
and ![]() for
for![]() , whereas
, whereas ![]() retains both energies close to the minimum.
retains both energies close to the minimum.
Figure 3 shows the effect of different parameter choices for an edge crossing the ridge of the screw. In this
![]()
![]()
Figure 1. Exact definition (left) and a coarse linear grid (right) of the screw surface example. The mesh contains 32 triangles, which results in an average mesh spacing of 10.85 times the minimum curvature radius of the geometry.
case, mere distance-based fitting yields a meandering curve, whereas energy-minimizing fitting straightens the path and removes undulations regardless of the chosen energy composition. As expected, the balanced energy mix, ![]() , yields a curve nestling in between the extreme cases of minimal stretch,
, yields a curve nestling in between the extreme cases of minimal stretch, ![]() , and minimal strain,
, and minimal strain,![]() . Yet these curves follow a rather similar path.
. Yet these curves follow a rather similar path.
Figure 4 illustrates the performance of the energy-minimizing fitting procedure with ![]() for the edge depicted in Figure 3. Starting with the straight edge, the normalized error functional assumes its maximum
for the edge depicted in Figure 3. Starting with the straight edge, the normalized error functional assumes its maximum![]() , while the normalized energies
, while the normalized energies ![]() and
and ![]() vanish after the first step. As a result of tapering
vanish after the first step. As a result of tapering ![]() both energies increase, thus allowing for error reduction. At the end of the process, the normalized error approaches zero and thus recovers the accuracy of single-step distance-based fitting. The energy functionals finally approach
both energies increase, thus allowing for error reduction. At the end of the process, the normalized error approaches zero and thus recovers the accuracy of single-step distance-based fitting. The energy functionals finally approach ![]() and
and![]() , respectively. The latter value indicates a significant strain reduction compared to the reference case. Note that
, respectively. The latter value indicates a significant strain reduction compared to the reference case. Note that ![]() is related to the curve length and thus dominated by surface curvature, which explains the comparably lower reduction.
is related to the curve length and thus dominated by surface curvature, which explains the comparably lower reduction.
Finally we look at the convergence behavior with respect to the fitting order![]() . Figure 5 depicts the
. Figure 5 depicts the ![]() errors of distance-based fitting and energy-minimizing fitting with
errors of distance-based fitting and energy-minimizing fitting with ![]() and
and![]() . The comparison shows only a negligible difference between the two graphs. In both cases the slope attains an asymptotic regime which indicates a linear dependence of the error exponent on the fitting order, i.e.,
. The comparison shows only a negligible difference between the two graphs. In both cases the slope attains an asymptotic regime which indicates a linear dependence of the error exponent on the fitting order, i.e.,![]() . Thus we conclude that the proposed energy-minimizing fitting procedure preserves the spectral convergence of the original, distance-based method.
. Thus we conclude that the proposed energy-minimizing fitting procedure preserves the spectral convergence of the original, distance-based method.
3.2. Scattered Surface Data
Scanning methods such as computed tomography (CT) or magnetic resonance imaging (MRI) provide scattered data that can be processed to give triangulated volume and surface representations of the investigated object. Here we consider a partition of a rabbit’s aortic arch, given as a fine mesh consisting of 24,644 triangles (Figure 6).
![]()
Figure 4. Evolution of the normalized error and energy functional for Curve 54 in course the energy-minimizing fitting procedure with ![]() using 100 steps.
using 100 steps.
![]()
Figure 5. Convergence of distance-based and energy-minimizing fitting with respect to the polynomial degree of curves.
![]()
Figure 6. Fine mesh (blue) of a rabbit aorta and coarse mesh used for fitting (red). Fine mesh courtesy of Spencer Sherwin, Imperial College London.
This representation was enhanced in two steps, yielding the “exact” surface: First, computing the vertex normals using the method of Max [18] . Second, constructing a cubic interpolant based on the point-normal vertex data in terms of the PN Triangles proposed by Vlachos et al. [19] . The projection ![]() of a point
of a point ![]() onto the surface is defined as the shortest projection along the Phong normal [20] , which is based on the linear mesh. For details we refer to [21] .
onto the surface is defined as the shortest projection along the Phong normal [20] , which is based on the linear mesh. For details we refer to [21] .
To evaluate the curve fitting methods we generated a curvature-dependent coarse mesh comprising 532 triangles (Figure 6). The ratio between the local mesh spacing and the radius of curvature was limited in order to allow for reasonable accuracy with moderate fitting order.
Starting from the linear mesh we constructed curves of order![]() . Figure 7 presents the curves after 50 fitting steps in comparison with the distance-based fitted curves in the high curvature bifurcation region. For clarity, the “exact” surface is also shown. In accordance with the previous test case the energy-minimizing fitting method yields straighter and shorter curves. In low curvature regions both methods result in nearly straight curves. This is not surprising, since a straight line is energetically optimal. Therefore, the computational cost can be reduced by applying energy-minimizing fitting only to those curves, which can be expected to profit from it. We explored a decision criterion based on the relative change in length
. Figure 7 presents the curves after 50 fitting steps in comparison with the distance-based fitted curves in the high curvature bifurcation region. For clarity, the “exact” surface is also shown. In accordance with the previous test case the energy-minimizing fitting method yields straighter and shorter curves. In low curvature regions both methods result in nearly straight curves. This is not surprising, since a straight line is energetically optimal. Therefore, the computational cost can be reduced by applying energy-minimizing fitting only to those curves, which can be expected to profit from it. We explored a decision criterion based on the relative change in length
![]() (14)
(14)
where ![]() is the length of the curve resulting from distance-based fitting and
is the length of the curve resulting from distance-based fitting and ![]() the length of the straight edge. Only when
the length of the straight edge. Only when ![]() exceeds a certain threshold
exceeds a certain threshold ![]() energy-minimizing fitting is performed. Table 1 compiles the results of distance-based fitting with energy-minimizing fitting using either no threshold (equivalent to
energy-minimizing fitting is performed. Table 1 compiles the results of distance-based fitting with energy-minimizing fitting using either no threshold (equivalent to![]() ) or
) or![]() . Note that the energy norm
. Note that the energy norm ![]() is adjusted by the value
is adjusted by the value![]() , which represents a mesh-dependent lower bound corresponding to the straight edges.
, which represents a mesh-dependent lower bound corresponding to the straight edges.
Remarkably, the energy-minimizing approach not only succeeds in reducing the energy norms, but also improves the approximation accuracy. Assuming a threshold of ![]() energy-minimized fitting is applied only to about ten percent of edges, which saves almost 90 percent of the computational cost. It is important to note that the improvements in energy and accuracy are not affected by this measure.
energy-minimized fitting is applied only to about ten percent of edges, which saves almost 90 percent of the computational cost. It is important to note that the improvements in energy and accuracy are not affected by this measure.
In addition we constructed triangular Bézier patches in two steps [21] : First, we inject the previously generated boundary curves. Second, we determine the inner control points by least-squares minimization of a distance functional. To assess the patch quality we consider the distortion measure![]() , which is based on the Jacobian of the mapping from parameter to physical space [5] . This measure has an upper bound of
, which is based on the Jacobian of the mapping from parameter to physical space [5] . This measure has an upper bound of ![]() corresponding to an isometric mapping, which is the preferred case. Smaller values indicate distorted patches and with
corresponding to an isometric mapping, which is the preferred case. Smaller values indicate distorted patches and with ![]() the mapping becomes invalid. As can be seen from Table 1, the energy-minimized curves lead to improved patches without further optimization. The quality measure
the mapping becomes invalid. As can be seen from Table 1, the energy-minimized curves lead to improved patches without further optimization. The quality measure ![]() increases by a factor of
increases by a factor of![]() , yielding
, yielding ![]() for all patches, which represents an acceptable quality for a high curvature geometry.
for all patches, which represents an acceptable quality for a high curvature geometry.
4. Conclusion
We investigated different techniques for fitting Bézier curves to surfaces as a first step of curvilinear mesh generation for high-order discretization methods. As a starting point we examined a distance-based least-squares fitting method. This method achieves a high accuracy, but tends to produce distorted curves where the mesh spacing is large compared to the radius of curvature. As remedy, we included approximations of stretch and bending energy into an incremental algorithm, resulting in an energy-minimizing fitting method. Both approaches were evaluated using two examples: an analytically defined screw surface and a surface triangulation of a rabbit aorta. The results confirm that the energy-minimizing method straightens and shortens the curves efficiently. Moreover the method preserves the accuracy and convergence behavior of distance-based fitting. In accordance with previous work (see e.g. [9] [11] [16] ), our study indicates that combining stretch and bending energy yields better results than using only one of those. Additionally, we analyzed the influence of the curve fitting method on
![]()
Figure 7. Comparison of fitting methods in the bifurcation of the rabbit aorta: dotted magenta lines distance-based, solid blue energy-minimizing with ![]() and
and ![]() steps.
steps.
patch construction. This investigation shows a clear improvement in patch quality when using energy-minimized curves. Nonetheless distortion remains an issue in the patch interior. Therefore, future work should address the extension of energy-minimizing approach to surface patch fitting.
Acknowledgements
The authors gratefully acknowledge the funding of this project by the German Research Foundation (DFG, STI 157/4-1).